Aufgaben zu Baumdiagramm und Pfadregeln

1
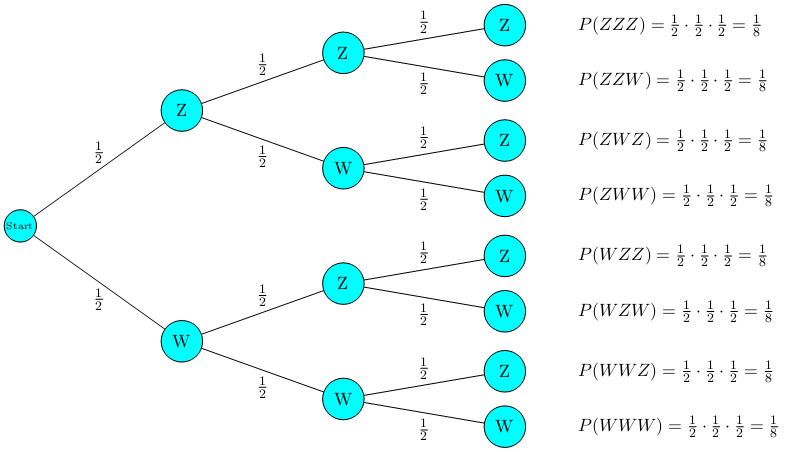
Zeichne den Baum für den dreifachen Münzenwurf Wappen(W) und Zahl(Z) und bestimme die Wahrscheinlichkeiten der einzelnen Ergebnisse.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm
2
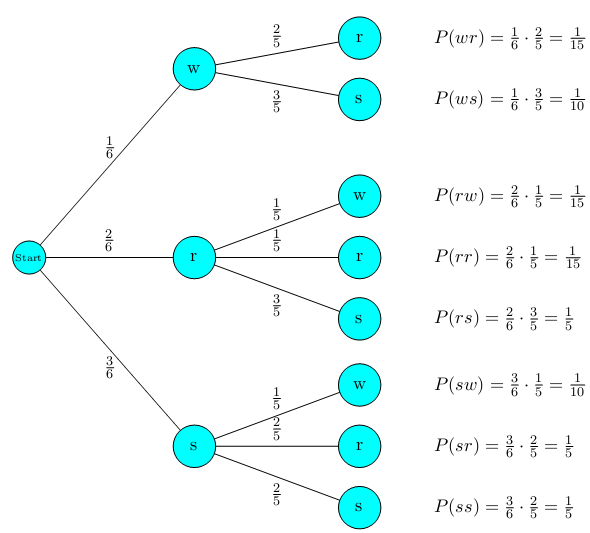
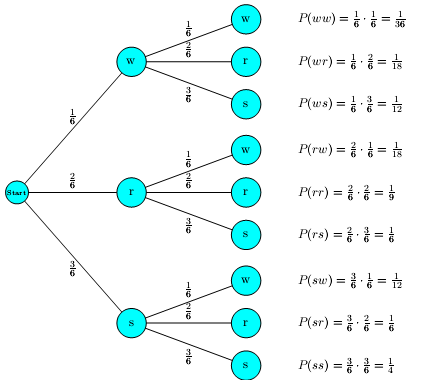
In einer Urne befinden sich 1 weiße, 2 rote und 3 schwarze Kugeln. Man zieht nacheinander zwei Kugeln einmal ohne Zurücklegen und einmal mit Zurücklegen der Kugel nach jedem Zug. Zeichne jeweils ein Baumdiagramm und gib einen Ergebnisraum und seine Mächtigkeit an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm
1. Ohne Zurücklegen
Schreibe die Ereignisse auf und die gib die Mächtigkeit der Menge an.
$\Omega$ = {(w,r), (w,s), (r,r), (r,w), (r,s), (s,s), (s,w), (s,r)}
$|\Omega|= 8$
2. Mit Zurücklegen
Schreibe die Ereignisse auf und die gib die Mächtigkeit der Menge an.
$\Omega$ = {(w,w), (w,s), (w,r), (r,r), (r,s), (r,w), (s,s), (s,r), (s,w)}
$|\Omega|= 9$
3
Max und Moritz streiten sich, wer das letzte Eis im Kühlschrank haben darf. Schließlich kommen sie zu dem Entschluss ihre Streitigkeit durch einen Münzwurf beizulegen.
Moritz gewinnt bei Kopf und Max bei Zahl.
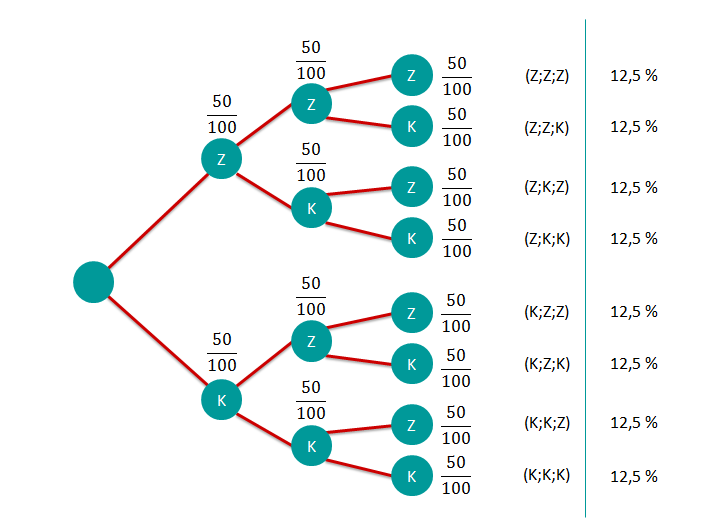
Löse die nachfolgenden Aufgaben mithilfe des nachfolgenden Baumdiagramms.
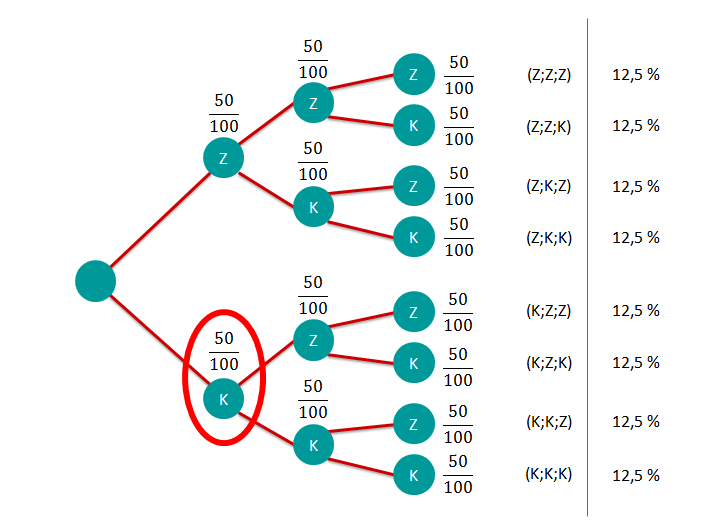
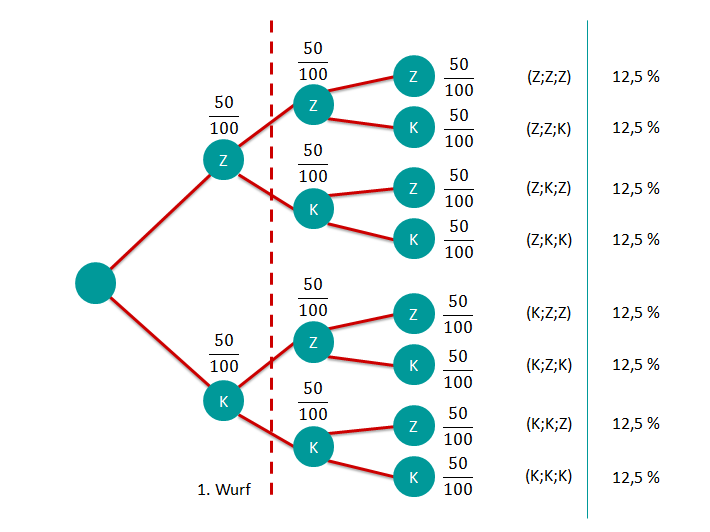
1. Mit welcher Wahrscheinlichkeit (in Prozent) gewinnt Moritz die erste Runde?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
  Wie man am Baumdiagramm ablesen kann, besteht eine Chance von 50%.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
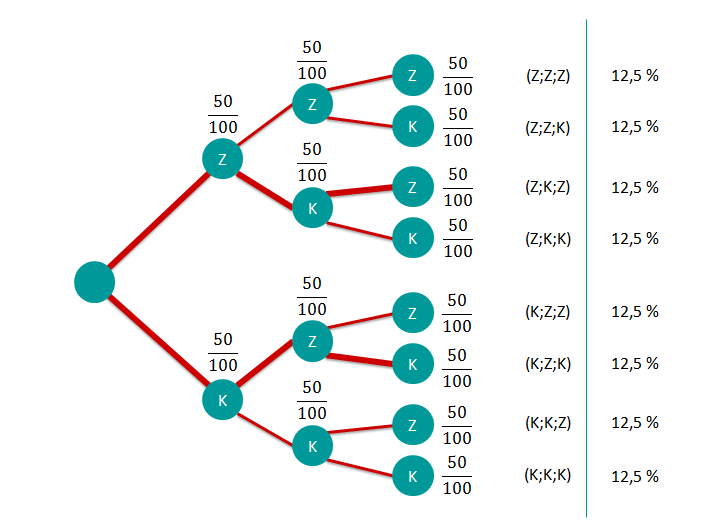
2. Nachdem Max die erste Runde gewonnen hat, fordert Moritz, dass derjenige gewinnt, der zwei von drei Runden gewinnt. Wie groß ist die Wahrscheinlichkeit, dass Moritz noch gewinnt?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
  Damit Moritz noch gewinnen kann muss er nun zweimal in Folge Kopf werfen.Nachdem der erste Wurf bereits erfolgt ist, muss der 2. und 3. Wurf Kopf sein.Die Warscheinlichkeit für Kopf beträgt jeweils $50\%\;=\;0{,}5$ Das heißt die Warscheinlichkeit für zweimal Kopf beträgt $0{,}5 \cdot 0{,}5 = 0{,}25 = 25\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
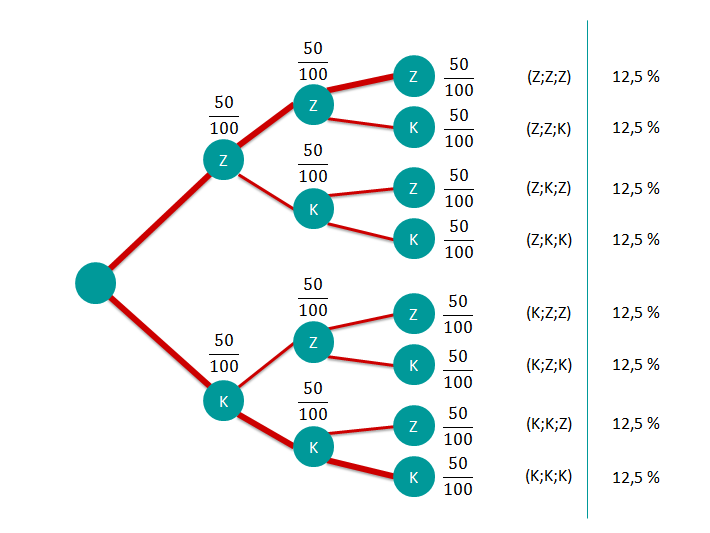
3. Max behauptet: "Es ist wahrscheinlicher, dass die Münze dreimal auf der selben Seite landet, als abwechselnd (bpsw. Kopf,Zahl,Kopf)
  Prüfe ob Max Recht hat, wenn nicht beweise das Gegenteil.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
  Die Behauptung stimmt nicht!
  Begründung:
  Dreimal die selbe Seite:
  Mithilfe der 2. Pfadregel kannst du nun die Wahrscheinlichkeit berechnen.
  $P(K,K,K) + P(Z,Z,Z) = 12{,}5\% + 12{,}5\% = 25\%$
  Abwechselnde Seiten: Dicke Pfade
  Mithilfe der 2. Pfadregel kannst du nun die Wahrscheinlichkeit berechnen.
  $P(K,Z,K) + P(Z,K,Z) = 12{,}5\% + 12{,}5\% = 25\%$
  Daraus folgt: Die Wahrscheinlichkeiten für die beiden Ereignisse sind genau gleich.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4
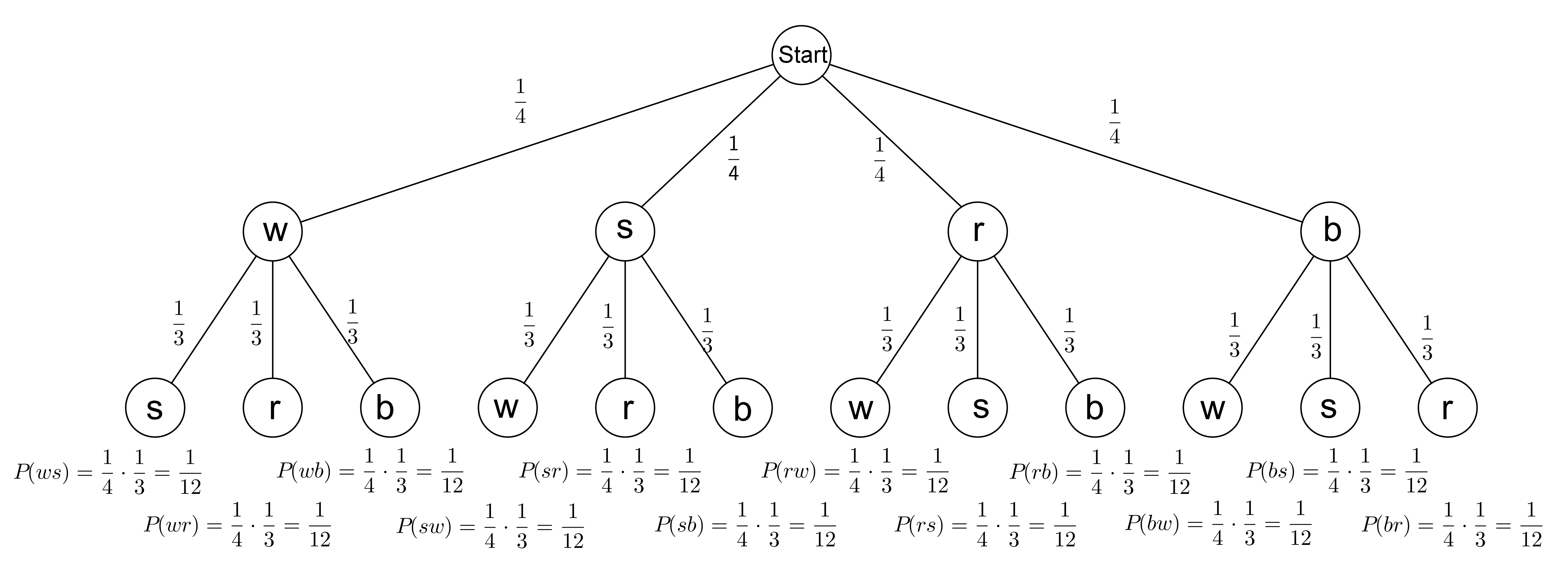
In einer Urne befinden sich eine weiße, eine schwarze, eine rote und eine blaue Kugel. Es werden nacheinander (und ohne Zurücklegen) zwei Kugeln entnommen.
1. Zeichne ein Baumdiagramm und lies den Ergebnisraum $\Omega$ dieses Zufallsexperiments ab.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm
  $\Omega=\{ws; wr; wb; sw; sr; sb; rw; rs; rb; bw; bs; br\}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Ermittle die Wahrscheinlichkeiten folgender Ereignisse:
  A: Keine der gezogenen Kugeln ist rot. B: Unter den gezogenen Kugeln ist eine rote. C: Es werden zwei rote Kugeln gezogen. D: Die gezogenen Kugeln sind weiß und schwarz.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm
  Ereignis A
  Es gibt 6 verschiedene Möglichkeiten, dafür, dass keine der gezogenen Kugeln rot ist.
  $A=\{ws; wb; sw; sb; bw; bs\}$
  $P(A)=P\left(ws\right)+P\left(wb\right)+P\left(sw\right)+P\left(sb\right)+P\left(bw\right)+P\left(bs\right)=\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}=\frac{6}{12}=0{,}5=50\%$
  Ereignis B
  Es gibt 6 Möglichkeiten dafür, dass eine rote unter den gezogenen Kugeln ist.
  $B=\{wr, sr; rw; rs; rb; br\}$
  $P(B)=P\left(wr\right)+P\left(sr\right)+P\left(rw\right)+P\left(rs\right)+P\left(rb\right)+P\left(br\right)=\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}=\frac{6}{12}=0{,}5=50\%$
  Ereignis C
  Das Ereignis C ist nicht möglich, weil keine zwei roten Kugeln in der Urne sind. Die Ereignismenge ist also leer.
  $C=\{\}$
  $P(C)=0=0\%$
  Ereignis D
  Es gibt zwei Möglichkeiten dafür, dass eine Kugel weiß und eine Kugel schwarz ist.
  $D=\{ws; sw\}$
  $P(D)=P\left(ws\right)+P\left(sw\right)=\frac{1}{12}+\frac{1}{12}=\frac{2}{12}\approx0{,}167=16{,}7\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Gib in Worten ein Ereignis E mit der Wahrscheinlichkeit $P(E)=25\ \%$ und ein Ereignis F mit der Wahrscheinlichkeit $P(F)=\frac{1}{3}$ an.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ereignisse bestimmen
  Wähle zum Beispiel folgende Ereignisse E und F:
  $E$ : "Die zweite gezogene Kugel ist weiß."
  $E=\{sw; rw; bw\}$
  $P(E)=P\left(sw\right)+P\left(rw\right)+P\left(bw\right)=\frac{1}{12}+\frac{1}{12}+\frac{1}{12}=\frac{3}{12}=25\ \%$
  $F$ : "Zuerst wird entweder weiß oder schwarz gezogen, danach entweder rot oder blau."
  $F=\{wr; wb; sr; sb\}$
  $P(F)=P\left(wr\right)+P\left(wb\right)+P\left(sr\right)+P\left(sb\right)=\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}=\frac{4}{12}=\frac{1}{3}\approx0.33=33\ \%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉