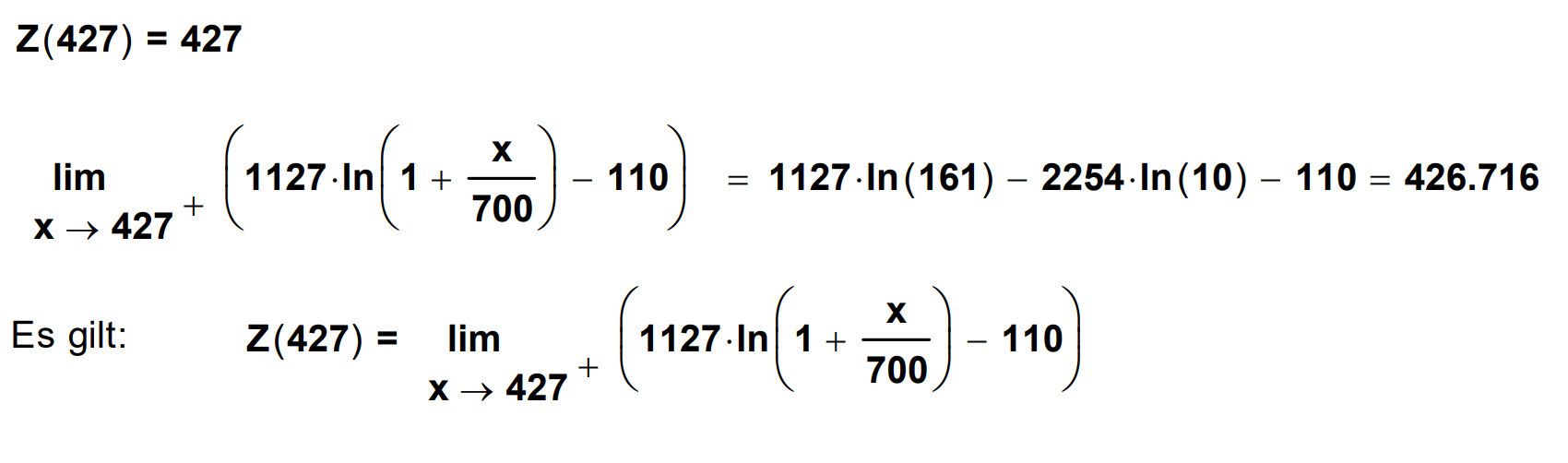A I
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
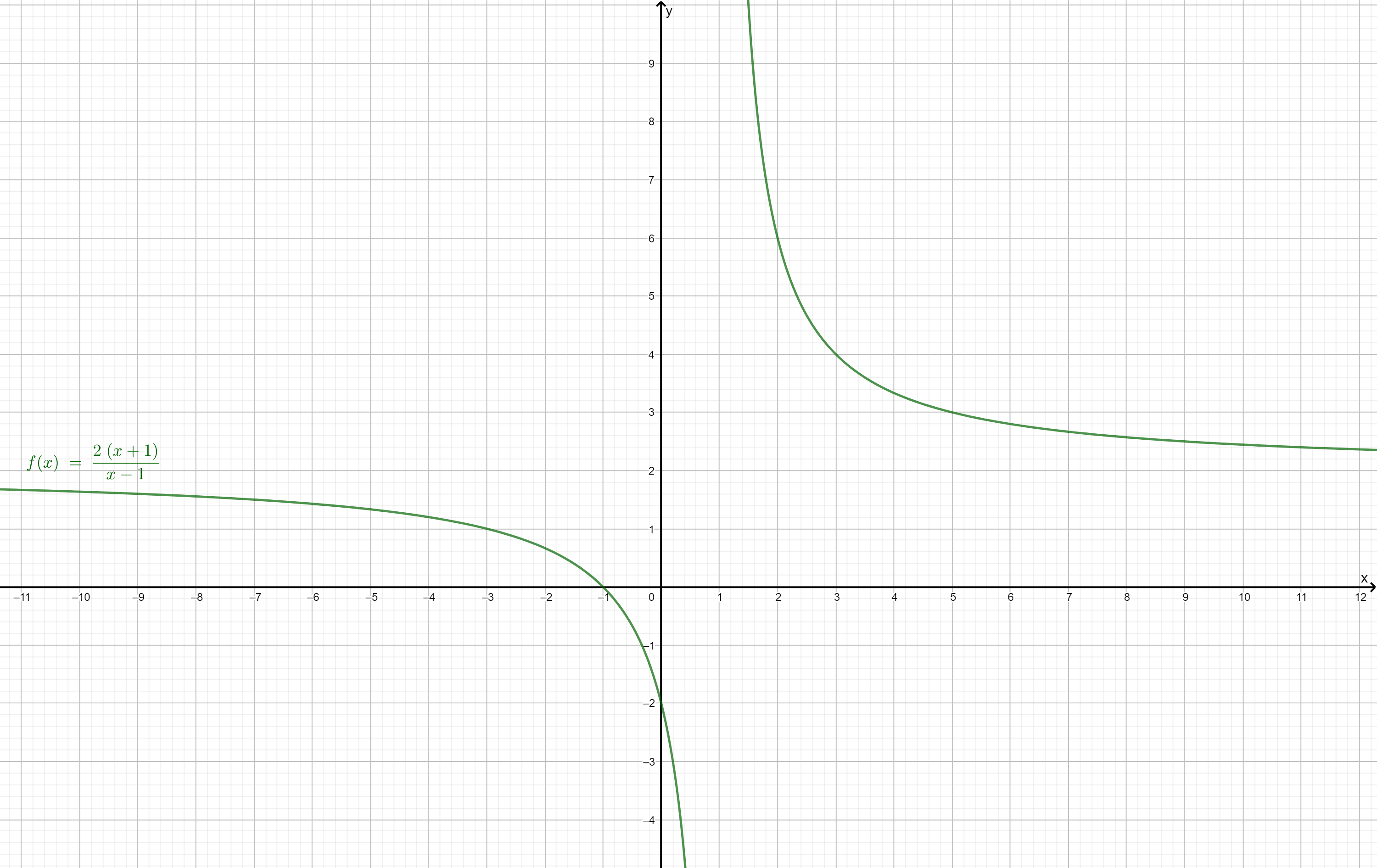
Gegeben ist die Funktion mit der maximalen Definitionsmenge .
Geben Sie an, prüfen Sie auf Nullstellen und folgern Sie daraus die Art der Definitionslücken. Untersuchen Sie das Verhalten der Funktionswerte bei Annäherung an die Definitionslücken. (7 BE)
Die Funktion mit ist die stetige Fortsetzung der Funktion (Nachweis nicht erforderlich). Ihr Graph wird mit bezeichnet.
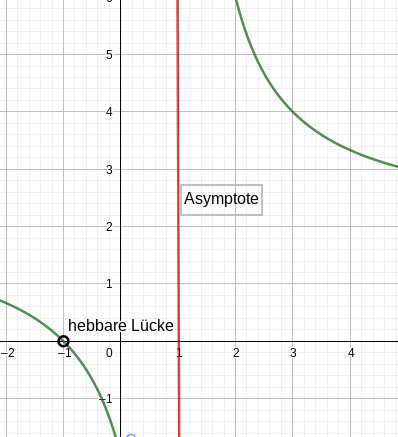
Geben Sie Art und Gleichungen aller Asymptoten von an und untersuchen Sie, ob sich der Graph der Funktion für der Asymptote von oben oder unten nähert. (5 BE)
Ermitteln Sie die maximalen Monotonieintervalle von f und geben Sie die Wertemenge von f an. (4 BE)
Zeichnen Sie und seine Asymptoten unter Berücksichtigung der bisherigen Ergebnisse für in ein kartesisches Koordinatensystem. (4 BE)
Der Graph , die -Achse und die Geraden und mit dem reellen Parameter begrenzen ein Flächenstück A. Kennzeichnen Sie diese Fläche für im Koordinatensystem von Teilaufgabe e) und berechnen Sie deren Flächenmaßzahl in Abhängigkeit von . (5 BE)
[mögliches Ergebnis: ]
Untersuchen Sie, ob für einen endlichen Wert annimmt. (2 BE)
Die Funktion ist eine Stammfunktion der Funktion Geben Sie nur mit den bisherigen Ergebnissen die maximalen Monotonieintervalle des Graphen der Funktion für an.
- 2
Die Funktion beschreibt näherungsweise die zeitliche Entwicklung der Einwohnerzahl einer fränkischen Kleinstadt. Es gilt hierfür die Funktionsgleichung mit , .
Der Zeitpunkt wird auf den 1.1.1995 festgelegt. Dabei gibt n die Einwohnerzahl in Tausend und die Zeit in Jahren an. Auf Einheiten soll bei den Rechnungen verzichtet werden. Runden Sie die Ergebnisse sinnvoll.
Am 1.1.1999 hatte die Stadt Einwohner. Bestimmen Sie damit den Wert des Parameters b. (2 BE)
[ Ergebnis: ]
Berechnen Sie Art und Koordinaten des lokalen Extrempunktes des Graphen der Funktion n und interpretieren Sie Ihre Ergebnisse im gegebenen Sachzusammenhang. (7 BE)
[ mögliches Teilergebnis: ]
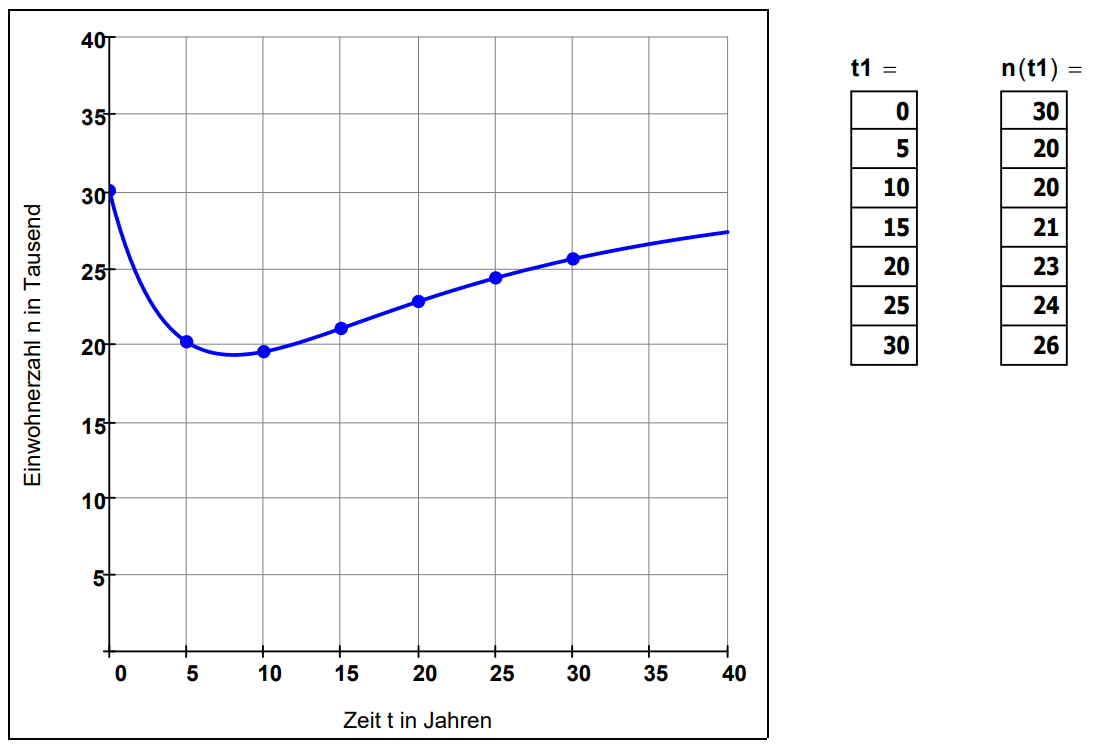
Zeichnen Sie den Graphen der Funktion n in ein geeignetes Koordinatensystem.
Zum 1.1.2010 konnte die Stadt Fördergelder beantragen. Diese richteten sich nach der durchschnittlichen Einwohnerzahl der Stadt während der vergangenen 15 Jahre. Ermitteln Sie die Höhe der Fördermittel, wenn es pro durchschnittlichem Einwohner an Fördergeldern gab, indem Sie zunächst das Integral berechnen. (5 BE)
[Teilergebnis: ]
- 3
Die subjektive Empfindung der Tonhöhe Z des menschlichen Gehörs in Abhängigkeit von der Frequenz in Hertz () kann durch folgende Gleichung beschrieben werden:
Die Einheit der Tonhöhe ist . Runden Sie die Ergebnisse auf ganze Zahlen. Auf das Mitführen von Einheiten kann verzichtet werden.
Zeigen Sie, dass die Funktion an der Nahtstelle - im Rahmen der Rundungsgenauigkeit - stetig und differenzierbar ist. (5 BE)
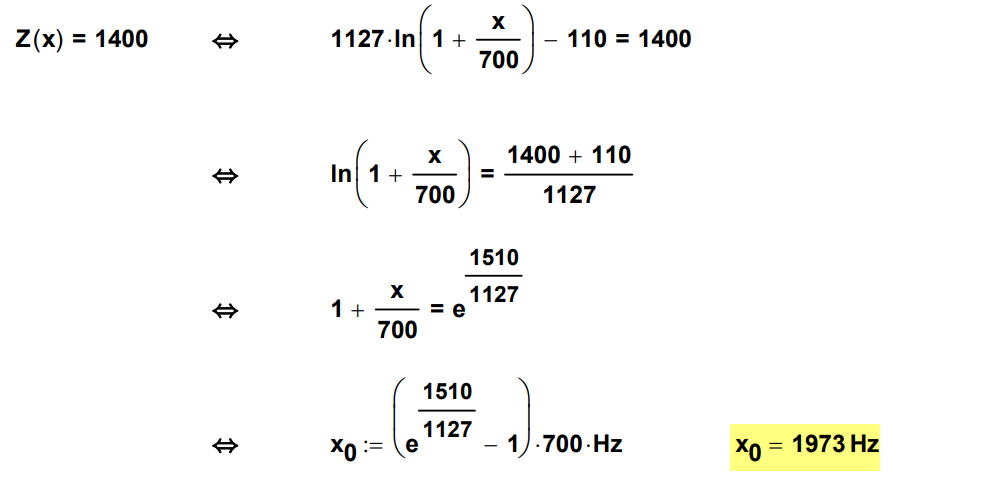
Berechnen Sie die Frequenz , bei der die Tonhöhe von empfunden wird. (3 BE)
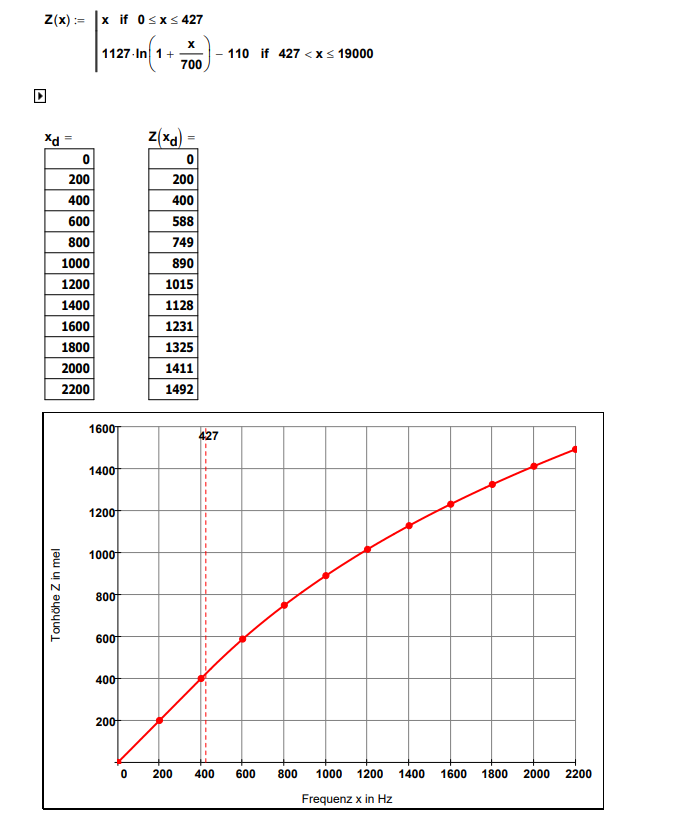
Zeichnen Sie den Graphen der Funktion im Bereich . (4 BE).
(Maßstab: waagrechte Achse: ; senkrechte Achse: )
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?