Stochastik, Teil A, Aufgabengruppe 1

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Betrachtet wird eine Bernoullikette mit der Trefferwahrscheinlichkeit 0,9 und der Länge 20. Beschreiben Sie zu dieser Bernoullikette ein Ereignis, dessen Wahrscheinlichkeit durch den Term $0{,}9^{20}+20\cdot0{,}1\cdot0{,}9^{19}$ angegeben wird. (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bernoulli-Kette
Hier muss man die allgemeine Form der Berechnung der Wahrscheinlichkeit bei einer Bernoullikette kennen. Diese lautet:
$B(n,p,k)=\begin{pmatrix}n\\k\end{pmatrix}\cdot p^k\cdot (1-p)^{n-k}$
Dabei wird $n$ als Länge der Bernoullikette bezeichnet, $k$ als Trefferzahl und $p$ als Trefferwahrscheinlichkeit und somit $1-p$ als Wahrscheinlichkeit für eine Niete.
Am 2. Summanden kann man die Zutaten besser zuordnen: Aus dem Exponenten 19 bei der Trefferwahrscheinlichkeit kann die Trefferzahl $k=19$ abgelesen werden. Demnach gibt es eine Niete. Der Binomialkoeffizient
$\begin{pmatrix}20\\19\end{pmatrix} =20$
passt dazu.
Dementsprechend handelt es sich beim 1. Summanden um die Wahrscheinlichkeit für 20 Treffer. Wegen
$\begin{pmatrix}20\\20\end{pmatrix} =1$
und $0{,}1^0=1$ bleibt hier nur der Faktor $0{,}9^{20}$ stehen. Insgesamt geht es also um die Wahrscheinlichkeit für 19 oder 20 Treffer. Das Ereignis heißt also "19 oder 20 Treffer" oder kurz gefasst: "Mindestens 19 Treffer".
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die Zufallsgröße X kann die Werte 0, 1, 2 und 3 annehmen. Die Tabelle zeigt die Wahrscheinlichkeitsverteilung von X mit $p_1, p_2 \in [0;1]$ .
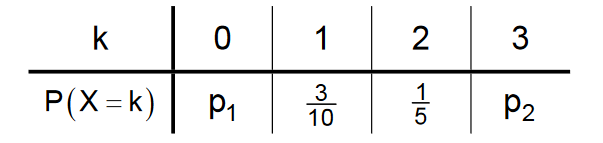
Zeigen Sie, dass der Erwartungswert von X nicht größer als 2,2 sein kann. (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert
Für den Erwartungswert $E(X)$ der Zufallsgröße $X$ ist bekannt:
Im vorliegenden Fall kann man die Summe konkret ausschreiben als:
Das es sich bei $X$ um eine Wahrscheinlichkeitsverteilung handelt, muss die Summe aller Einzelwahrscheinlichkeiten gleich $1$ sein:
Da $p_1$ im Erwartungswert ohnehin mit Wert der Zufallsgröße 0 multipliziert wird, kann man $p_1$ mit 0 ansetzen, so dass für $p_2$ ein möglichst großer Betrag übrig bleibt: $p_2=0{,}5$ . Für den Fall ist der Erwartungswert:
Der Erwartungswert ist also maximal 2,2. Er kann nicht größer als 2,2 werden!
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
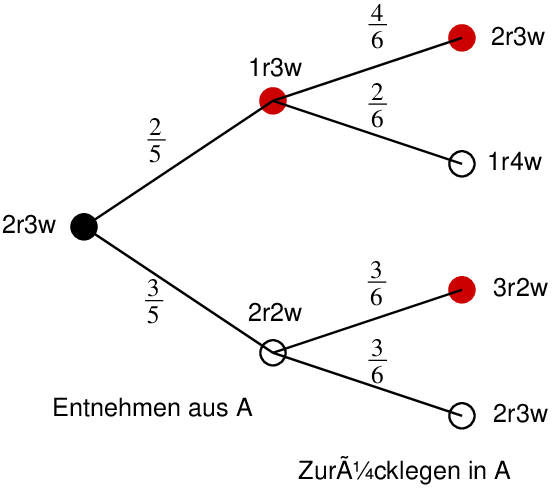
In Urne A befinden sich zwei rote und drei weiße Kugeln. Urne B enthält drei rote und zwei weiße Kugeln. Betrachtet wird folgendes Zufallsexperiment:
Aus Urne A wird eine Kugel zufällig entnommen und in Urne B gelegt; danach wird aus Urne B eine Kugel zufällig entnommen und in Urne A gelegt.
1. Geben Sie alle Möglichkeiten für den Inhalt der Urne A nach der Durchführung des Zufallsexperiments an. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm
  Bei dieser Aufgabe kommt es darauf an, systematisch vorzugehen, um keinen Fall zu übersehen.
  Beim Griff in Urne A kann man eine rote oder eine weiße Kugel erwischen. Nach dem Transfer in Urne B nimmt man aus Urne B eine Kugel und kann auch dabei wieder eine rote oder eine weiße Kugel erhalten.
  Zu jedem der zwei Fälle beim Entnehmen aus A gibt es zwei Fälle des Zurücklegens in A. Das kann z. B. in einem Baumdiagramm dargestellt werden:
  Man sieht daran, dass der Urneninhalt in zwei Fällen letztlich unverändert bleibt und in zwei Fällen eine Umwandlung der Farbe erfolgt.
  Die Wahrscheinlichkeiten im 2. Teil des Experiments werden in Sechstel gemessen, denn in der Urne B sind ja mittlerweile $6$ Kugeln!
  Der Inhalt von Urne A kann demnach $2r3w$ (also unverändert 2-mal rot, 3-mal weiß), $1r4w$ oder $3r2w$ sein.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Betrachtet wird das Ereignis $E:$ „Nach Durchführung des Zufallsexperiments befinden sich wieder drei weiße Kugeln in Urne A.“ Untersuchen Sie, ob das Ereignis $E$ eine größere Wahrscheinlichkeit als sein Gegenereignis hat. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Gegenereignis
  Das Gegenereignis zu $E$ wird mit $\overline E$ bezeichnet, die ausführliche sprachliche Formulierung lautet: "Nach Durchführung des Zufallsexperiments befinden sich nicht wieder 3 weiße Kugeln in der Urne", oder positiv formuliert:
  Nach Durchführung des Zufallsexperiments befinden sich 2 oder 4 weiße Kugeln in der Urne.
  Die Wahrscheinlichkeit für das Ereignis $E$ setzt sich aus zwei Experimentverläufen zusammen, entsprchend zwei Pfaden im Baumdiagramm. Wenn mann weiß, dass entlang eines Pfades die Wahrscheinlichkeiten zu multiplizieren sind (1. Pfadregel) und die Wahrscheinlichkeiten für zwei verschiedene Pfade addiert werden müssen (2. Pfadregel), ergibt sich:
  $P(E)= \frac25\cdot\frac46 + \frac35\cdot\frac36 = \frac{8}{30}+\frac{9}{30}= \frac{17}{30}$
  Das Gegenereignis $\overline{E}$ hat somit die Wahrscheinlichkeit $P(\overline{E})=1-P(E) = 1-\frac{17}{30}=\frac{13}{30}$ .
  Das Ereignis $E$ hat also die größere Wahrscheinlichkeit als sein Gegenereignis!
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Stochastik, Teil A, Aufgabengruppe 1

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?