Berechnen Sie den Abstand der parallelen Geraden g: und h: .
Rundet das Ergebnis auf zwei Stellen nach dem Komma.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Abstand zweier Geraden
Abstand zweier paralleler Geraden
Der kürzeste Weg zwischen zwei parallelen Geraden ist eine Normale der Geraden .
Der Abstand der Geraden entspricht dem Abstand zwischen den beiden Schnittpunkten der Normale mit den Geraden .
Skizze
Fertige eine Skizze an.
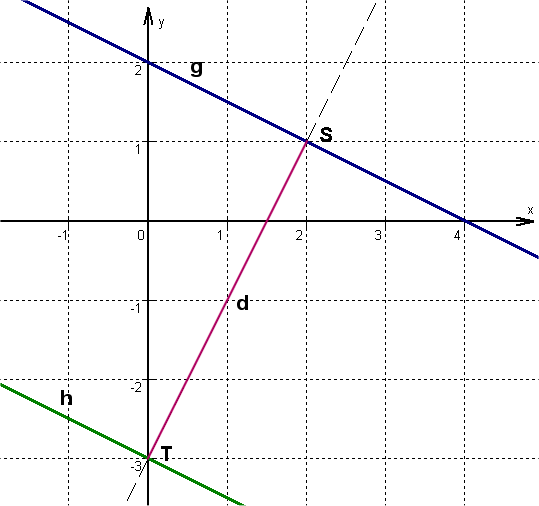
| ↓ | Setze die Steigung der Funktion (nämlich ) ein. | ||
| ↓ | Vereinfache die rechte Seite. | ||
Stelle nun die Geradengleichung auf.
Es wird ein Punkt T, der auf der Geraden liegt benötigt. Verwendet wird der y-Abschnitt von : .
Setze (siehe Skizze) und in die allgemeine Geradengleichung ein um t zu bestimmen.
| ↓ | |||
| ↓ | Setze t und in die allgemeine Geradengleichung ein. | ||
Bestimme den Schnittpunkt von d und g
Berechne zunächst die x-Koordinate des Schnittpunkts S.
Normale d:
Gerade g:
Setze die Funktionen gleich.
Berechne nun die y-Koordinate des Schnittpunkts S.
| ↓ | Setze das gefundene x = 2 ein. | ||
| ↓ | Rechne aus. | ||
Gib die Koordinaten des Schnittpunktes S an.
Bestimme den Abstand der Punkte S und T.
Bestimme den Abstand in x-Richtung.
,
Berechne die Differenz der x-Werte von S und T.
Bestimme den Abstand in y-Richtung.
,
Berechne die Differenz der y-Werte.
Bestimme den Abstand in direkter Linie zwischen den Punkten.
Wende den Satz des Pythagoras an.
| ↓ | Berechne die beiden Potenzen. | ||
| ↓ | Addiere. | ||
| ↓ | Ziehe die Wurzel. | ||
Wenn du in den Taschenrechner eingibst und das Ergebnis auf zwei Stellen nach dem Komma rundest, erhältst du:
Ergebnis
Der Abstand der beiden Geraden beträgt etwa 4,47.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
