Aufgaben zu parallelen und senkrechten Geraden, Abständen u. a.

Hier findest du gemischte Aufgaben zu Geraden. Lerne, Geradengleichungen zu parallelen und senkrechten Geraden anzugeben und Abstände zu berechnen.

1
Bestimme die Gleichung der Geraden, die durch den Punkt P geht und senkrecht zur gegebenen Gerade steht.
1. $y=3x+2$
  $P(3|5)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
  Bestimme zunächst die Steigung der zu $g(x):y=3x+2$ senkrechten Geraden $h$ mit der Formel.
  $\displaystyle m_2=-\frac1{m_1}$
  Setz den Wert ein.
  $\displaystyle m_2=-\frac1{3}$
  Die gesuchte Senkrechte hat also Steigung $\displaystyle-\frac13$ .
  Bestimme nun den y-Achsenabschnitt der Senkrechten $h$ mit dem gegebenen Punkt $P(3|5)$ , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
  $h(x_p):y_p=m_2 x_p+b$
  Setze die Werte ein.
  $5=-\frac13\cdot3+b\;\;\;\left|+1\right.$
  Vereinfache und addiere $1$ .
  $6=b\Leftrightarrow b=6$
  Also lautet die gesuchte Geradengleichung $\displaystyle h(x):y=-\frac13x+6$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $y=0{,}5x+1$
  $P(1|2)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
  Bestimme zunächst die Steigung der zu $g(x):y=0{,}5x+1$ senkrechten Geraden $h$ mit der Formel.
  $m_2=\displaystyle -\frac1{m_1}$
  Setz den Wert ein.
  $\displaystyle m_2=-\frac1{0{,}5}=-\frac1{\frac12}=-2$
  Die gesuchte Senkrechte hat also Steigung $-2$ .
  Bestimme nun den y-Achsenabschnitt der Senkrechten $h$ mit dem gegebenen Punkt $P(1|2)$ , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
  $h(x_p):y_p=m_2 x_p+b$
  Setz die Werte ein.
  $2=-2\cdot 1+b$ $|+2$
  Vereinfache und addiere 2.
  $4=b\Rightarrow b=4$
  Also lautet die gesuchte Geradengleichung $h(x):y=−2x+4$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $y=-5x+6$
  $P(-10|1)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
  Bestimme zunächst die Steigung der zu $g(x):y=-5x+6$ senkrechten Geraden $h$ mit der Formel.
  $\displaystyle m_2=-\frac1{m_1}$
  Setz den Wert ein.
  $\displaystyle m_2=-\frac1{-5}=0{,}2$
  Die gesuchte Senkrechte hat also Steigung $0{,}2$ .
  Bestimme nun den y-Achsenabschnitt der Senkrechten $h$ mit dem gegebenen Punkt $P(-10|1)$ , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
  $h(x_p):y_p=m_2 x_p+b$
  Setz die Werte ein.
  $1=0{,}2\cdot(-10)+b$ $|+2$
  Vereinfache und addiere 2.
  $3=b\Rightarrow b=3$
  Also lautet die gesuchte Geradengleichung $h(x):y=0{,}2x+3$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $y=4x+3$
  $P(2|-5)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
  Bestimme zunächst die Steigung der zu $g(x):y=4x+3$ senkrechten Geraden $h$ mit der Formel.
  $\displaystyle m_2=-\frac1{m_1}$
  Setz den Wert ein.
  $m_2=-\displaystyle\frac14=-0{,}25$
  Die gesuchte Senkrechte hat also Steigung $-0{,}25$ .
  Bestimme nun den y-Achsenabschnitt der Senkrechten $h$ mit dem gegebenen Punkt $P(2|-5)$ , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
  $h(x_p):y_p=m_2 x_p+b$
  Setz die Werte ein.
  $-5=-0{,}25\cdot2+b$ $+0{,}5$
  Vereinfache und addiere 0,5.
  $-4{,}5=b\Rightarrow b=-4{,}5$
  Also lautet die Geradengleichung $h(x):y=-0{,}25x-4{,}5$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. $y=-\frac23x+2$
  $P(4|6)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
  Bestimme zunächst die Steigung der zu $g(x):y=-\frac23x+3$ senkrechten Geraden $h$ mit der Formel.
  $\displaystyle m_2=-\frac1{m_1}$
  Setz den Wert ein.
  $\displaystyle m_2=-\frac1{-\frac23}=\frac32$
  Die gesuchte Senkrechte hat also Steigung $\displaystyle\frac32$ .
  Bestimme nun den y-Achsenabschnitt der Senkrechten $h$ mit dem gegebenen Punkt $P(4|6)$ , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
  $h(x_p):y_p=m_2x_p+b$
  Setz die Werte ein.
  $\displaystyle6=\frac32\cdot4+b$ $|-6$
  Vereinfache und subtrahiere 6.
  $0=b\Rightarrow b=0$
  Also lautet die Geradengleichung $\displaystyle h(x):y=\frac32x$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. $y=\frac13x-2$
  $P(2|5)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
  Bestimme zunächst die Steigung der zu $\displaystyle g(x):y=\frac13x-2$ senkrechten Geraden $h$ mit der Formel.
  $m_2=\displaystyle-\frac1{m_1}$
  Setz den Wert ein.
  $m_2=\displaystyle -\frac1{\frac13}=-3$
  Die gesuchte Senkrechte hat also Steigung $-3$ .
  Bestimme nun den y-Achsenabschnitt der Senkrechten $h$ mit dem gegebenen Punkt $P(2|5)$ , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
  $h(x_p):y_p=m_2x_p+b$
  Setz die Werte ein.
  $5=-3\cdot2+b$ $|+6$
  Vereinfache und addiere 6.
  $11=b\Rightarrow b=11$
  Also lautet die Geradengleichung $h(x):y=−3x+11$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Bestimme die Gleichung der Geraden g, die parallel zur Geraden h ist und durch den Punkt P geht.
1. h: $y=3x-2$ ; P(1|0) $\;$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung bestimmen
  $y=3x-2$ ; P(1|0)
  Damit die gesuchte Gerade parallel zu h ist, muss sie die selbe Steigung besitzen.
  Die Steigung einer Gerade ist m der allgemeinen Geradengleichung.
  $m=3$
  Geradengleichung aufstellen
  Setze m (3) und P(1|0) in die allgemeinen Geradengleichung ein.
  $\displaystyle 0$ $=$ $\displaystyle 3\cdot1+t$ $\displaystyle {-3}$
  ↓
  Gleichung nach t auflösen.
  $\displaystyle t$ $=$ $\displaystyle -3$
  Setze m und t in die allgemeinen Geradengleichung ein.
  $\;\;\Rightarrow\;\;$ Geradengleichung: $y=3x-3$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. h: $y=x-4$ ; P(1|2) $\;$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung bestimmen
  $y=x-4$ ; P(1|2)
  Damit die gesuchte Gerade parallel zu h ist, muss sie die selbe Steigung besitzen.
  Die Steigung einer Gerade ist m der allgemeinen Geradengleichung.
  $m=1$
  Gleichung aufstellen
  Setze m (1) und P(1|2) in die allgemeinen Geradengleichung ein.
  $\displaystyle 2$ $=$ $\displaystyle 1+t$ $\displaystyle −1$
  ↓
  Gleichung nach t auflösen.
  $\displaystyle t$ $=$ $\displaystyle 1$
  Setze m und t in die allgemeinen Geradengleichung ein.
  $\;\;\Rightarrow\;\;$ Geradengleichung: $y=x+1$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. h: $y=4x$ ; P(5|18) $\;$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung bestimmen
  $y=4x$ ; P(5|18)
  Damit die gesuchte Gerade parallel zu h ist, muss sie die selbe Steigung besitzen.
  Die Steigung einer Gerade ist m der allgemeinen Geradengleichung.
  $m=4$
  Gleichung aufstellen
  Setze m (4) und P(5|18) in die allgemeinen Geradengleichung ein.
  $\displaystyle 18$ $=$ $\displaystyle 4\cdot5+t$ $\displaystyle -20$
  ↓
  Gleichung nach t auflösen.
  $\displaystyle t$ $=$ $\displaystyle -2$
  Setze m und t in die allgemeinen Geradengleichung ein.
  $\;\;\Rightarrow\;\;$ Geradengleichung: $y=4x-2$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. h: $y=-2x+1$ ; P(-1|4)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung bestimmen
  $y=-2x+1$ ; P(-1|4)
  Damit die gesuchte Gerade parallel zu h ist, muss sie die selbe Steigung besitzen.
  Die Steigung einer Gerade ist m der allgemeinen Geradengleichung.
  $m=-2$
  Gleichung aufstellen
  Setze m (-2) und P(-1|4) in die allgemeinen Geradengleichung ein.
  $\displaystyle 4$ $=$ $\displaystyle −2⋅(−1)+t$ $\displaystyle -2$
  ↓
  Gleichung nach t auflösen.
  $\displaystyle t$ $=$ $\displaystyle 2$
  Setze m und t in die allgemeinen Geradengleichung ein.
  $\;\;\Rightarrow\;\;$ Geradengleichung: $y=-2x+2$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
Bestimme die Gleichung der Geraden, die durch …
1. den Punkt $P(-3 | 4)$ geht und parallel ist zur $x$ -Achse.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  Parallel zur $x$ -Achse, das heißt die gleiche Steigung wie die $x$ -Achse, also $m = 0$ .
  $m$ und $P$ in die allgemeine Geradengeleichung einsetzen.
  Zur Geradengleichung zusammensetzen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. den Punkt $Q(2 | 5)$ geht und parallel ist zur Winkelhalbierenden des 2.Quadranten.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  Parallel zur Winkelhalbierenden des 2. Quadranten bedeutet gleiche Steigung.
  Die Steigung der Winkelhalbierenden des 2. Quadranten ist -1
  $m$ in die Geradengleichung einsetzen und damit $t$ berechnen.
  $m$ und $t$ in die allgemeine Geradengleichung einsetzen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. den Punkt $R(-4|2)$ geht und parallel ist zur $y$ -Achse.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  Parallel zur $y$ -Achse, d.h. keine Funktionsgleichung, da einem $x$ -Wert unendlich viele $y$ -Werte zugeordnet werden. Die Gerade kann also nur als der $x$ -Wert von $R$ beschrieben werden.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. den Punkt $S(2 |-3)$ geht und parallel ist zur Winkelhalbierenden des 1.Quadranten.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  Parallel zur Winkelhalbierenden des 1. Quadranten bedeutet die gleiche Steigung.
  Die Steigung der Winkelhalbierenden des 1. Quadranten ist 1.
  Setze m und S in die allgemeine Geradengleichung ein und löse nach $t$ auf.
  Setze $m$ und $t$ in die allgemeine Geradengleichung ein.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. den Ursprung geht und parallel ist zur Geraden $\overline{\mathrm{AB}}$ mit $A(-72|-60)$ und $B(-24|-20)$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  Durch den Ursprung, das heißt $y$ -Achsenabschnitt $t=0$
  Parallel zur Geraden $\overline{\mathrm{AB}}$ , bedeutet die gesuchte Gerade hat die gleiche Steigung wie $\overline{\mathrm{AB}}$ .
  Berechne die Steigung $m$ mithilfe des Differenzenquotienten .
  Setze $m$ und $t$ in die allgemeine Geradengleichung ein.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Zwei aufeinander senkrecht stehende Geraden schneiden sich in $S\left(-2|-1\right)$ .
Geben Sie mögliche Geradengleichungen an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Wir haben zwei zueinander senkrechte Geraden mit dem Schnittpunkt $(-2,-1)$ . Wie man aus der Angabe schon rauslesen kann, gibt es mehrere Möglichkeiten, zwei solcher Geraden zu wählen. Im Folgenden wird eine Möglichkeit angegeben. Ein gutes Kriterium, um zu überprüfen, ob die zwei gewählten Geraden senkrecht zueinander sind, ist folgendes:
$m_{1} \cdot m_{2}=-1$ .
Wähle zum Beispiel die Geraden g mit $y=g(x)=x+1$ und h mit $y=h(x)=-x-3$ . Dann gilt $m_{1} \cdot m_{2}=1\cdot(-1)=-1$ und es gilt $g(-2)=-1$ und $h(-2)=-1$ . Also liegt der Schnittpunkt auf den beiden Geraden und diese sind senkrecht zueinander.
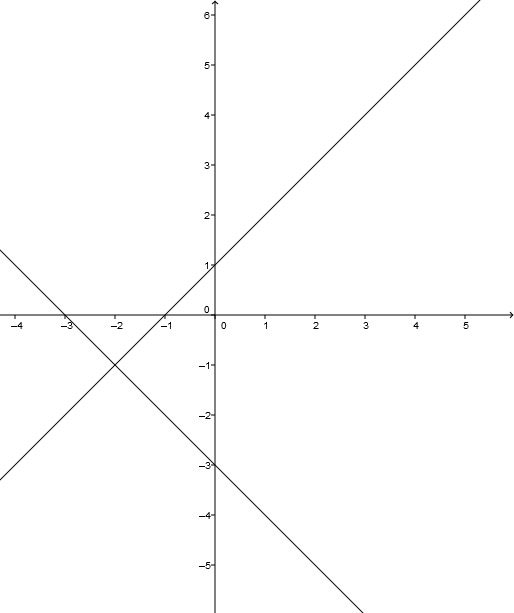
Achtung:
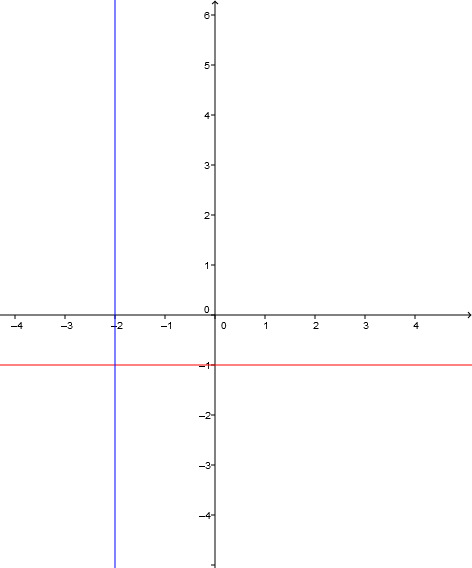
Wählst du zum Beispiel die Gerade $y=-1$ (eine Parallele zur x-Achse), die durch den Punkt $(-2,-1)$ geht, gibt es genau eine Gerade, nämlich die Gerade, die parallel zur y-Achse steht mit der Geradengleichung $x=-2$ . Diese stehen zwar senkrecht aufeinander, aber $x=-2$ ist keine Funktion, sondern eine Relation.

Berechne den Abstand der Geraden zum Ursprung.

$y=\frac34x-5$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung der Senkrechten

Geradensteigung und Geradengleichung

Der kürzeste Abstand zum Ursprung ist die Senkrechte auf die Gerade durch den Ursprung. Ist $g(x):y=m_1\cdot x+b$ , so berechnest du die Steigung der Senkrechten $m_2$ mit der Formel.

$\displaystyle m_2=-\frac1{m_1}$

Setz den Wert der Steigung ein.

$\displaystyle m_2=-\frac{1}{\frac34}=-\frac43$

Die gesuchte Senkrechte hat also Steigung $-\displaystyle\frac43$ und geht durch den Ursprung, der y-Achsenabschnitt $b$ ist also 0. Damit lautet die Geradengleichung der Senkrechte $\displaystyle h(x):y=-\frac43 x$ .

Berechne nun den Schnittpunkt $A \,(x_s|y_s)$ der beiden Geraden indem du ihre Geradengleichungen gleichsetzt.

$\displaystyle g\left(x_s\right)$	$=$	$\displaystyle h\left(x_s\right)$
	↓	Setz die Geradengleichungen ein.
$\displaystyle -\frac{4}{3}x_s$	$=$	$\displaystyle \frac{3}{4}x_s-5$	$\displaystyle -\frac{3}{4}x_s$
	↓	Bringe die Variable $x_s$ auf die linke Seite.
$\displaystyle \displaystyle-\frac{25}{12}x_s$	$=$	$\displaystyle -5$	$\displaystyle \cdot(-1)$
$\displaystyle \displaystyle\frac{25}{12}x_s$	$=$	$\displaystyle 5$	$\displaystyle :\frac{25}{12}$
$\displaystyle x_s$	$=$	$\displaystyle \frac{12}{5}$
	$=$	$\displaystyle 2{,}4$

Setz nun $x_s$ in eine der Geradengleichungen ein um $y_s$ zu bestimmen.

$\displaystyle h(x_s):y_s=-\frac43x_s$

Setz $x_s=2{,}4$ ein.

$\displaystyle y_s=-\frac43\cdot2{,}4=-3{,}2$

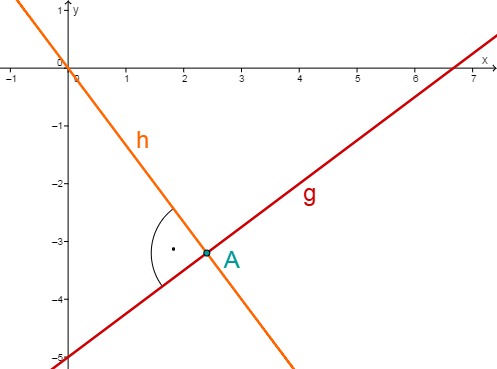
Der Schnittpunkt der Geraden $h$ und $g$ liegt also bei $A\,(2{,}4|-3{,}2)$ .

Bestimme nun den Abstand des Ursprungs zum berechneten Schnittpunkt $A$ , dies ist genau der kürzeste Abstand der Geraden $g$ zum Ursprung.

$\displaystyle d=\sqrt{(x_s-x_0)^2+(y_s-y_0)^2}$

Setz die Werte ein.

$\displaystyle d=\sqrt{(2{,}4-0)^2+(-3{,}2-0)^2}$

Vereinfache.

$\displaystyle =\sqrt{5{,}76+10{,}24}=\sqrt{16}=4$

Der kürzeste Abstand der Geraden $g$ zum Ursprung ist also 4.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$y=-\frac12x+2$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung

Der kürzeste Abstand zum Ursprung ist die Senkrechte auf die Gerade durch den Ursprung. Ist $g(x):y=m_1⋅x+b$ , so berechnest du die Steigung der Senkrechten $m_2$ mit der Formel

$\displaystyle m_2=-\frac1{m_1}$

Setz den Wert der Steigung ein.

$\displaystyle m_2=-\frac{1}{-\frac12}=2$

Die gesuchte Senkrechte hat also Steigung $2$ und geht durch den Ursprung, der y-Achsenabschnitt $b$ ist also 0. Damit lautet die Geradengleichung der Senkrechte $h(x):y=2x$ .

Berechne nun den Schnittpunkt $A\,(x_s|y_s)$ der beiden Geraden, indem du ihre Geradengleichungen gleichsetzt.

$\displaystyle g\left(x_s\right)$	$=$	$\displaystyle h\left(x_s\right)$
	↓	Setz die Geradengleichungen ein.
$\displaystyle \displaystyle -\frac12x_s+2$	$=$	$\displaystyle 2x_s$	$\displaystyle -2x_s$
	↓	Bringe die Variable $x_s$ auf die linke Seite.
$\displaystyle -2{,}5x_s+2$	$=$	$\displaystyle 0$	$\displaystyle -2$
	↓	Bringe die 2 auf die rechte Seite.
$\displaystyle -2{,}5x_s$	$=$	$\displaystyle -2$	$\displaystyle :\left(-2{,}5\right)$
$\displaystyle x_s$	$=$	$\displaystyle 0{,}8$

Setz nun $x_s$ in eine der Geradengleichungen ein um $y_s$ zu bestimmen.

$h(x_s):y_s=2x_s$

Setz $x_s=0{,}8$ ein.

$y_s=2\cdot0{,}8=1{,}6$

Der Schnittpunkt der Geraden $h$ und $g$ liegt also bei $A\,(0{,}8|1{,}6)$ .

Bestimme nun den Abstand des Ursprungs zum berechneten Schnittpunkt $A$ , dies ist genau der kürzeste Abstand der Geraden $g$ zum Ursprung.

$\displaystyle d=\sqrt{(x_s-x_0)^2+(y_s-y_0)^2}$

Setz die Werte ein.

$d=\sqrt{(0{,}8-0)^2+(1{,}6-0)^2}$

Vereinfache.

$=\sqrt{0{,}64+2{,}56}=\sqrt{3{,}2}\approx 1{,}79$

Der kürzeste Abstand der Geraden $g$ zum Ursprung ist also etwa $1{,}79$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Berechnen Sie den Abstand der parallelen Geraden g: $y=-\frac12x+2$ und h: $y=-\frac12x-3$ .

Rundet das Ergebnis auf zwei Stellen nach dem Komma.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Abstand zweier Geraden

Abstand zweier paralleler Geraden

Der kürzeste Weg zwischen zwei parallelen Geraden ist eine Normale der Geraden .

Der Abstand der Geraden entspricht dem Abstand zwischen den beiden Schnittpunkten der Normale mit den Geraden .

Skizze

Fertige eine Skizze an.

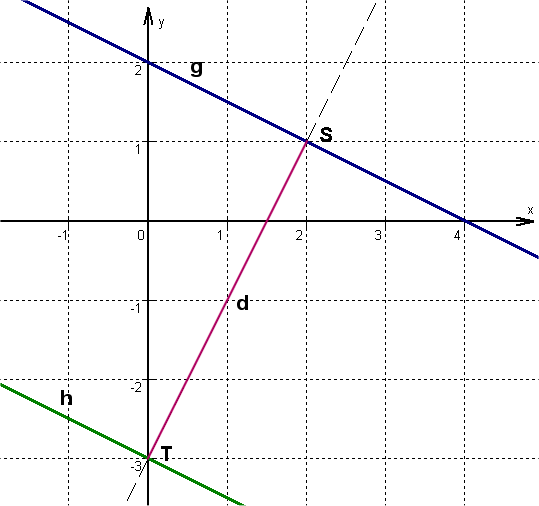
Graph Geraden Parallelen Abstand zwischen den Parallelen

Geradengleichung

Stelle die Geradengleichung der Normalen d auf.

Berechne dazu zunächst die Steigung.

$\displaystyle m_d\cdot m_g$	$=$	$\displaystyle -1$	$\displaystyle :m_g$
$\displaystyle m_d$	$=$	$\displaystyle \frac{-1}{m_g}$
	↓	Setze die Steigung der Funktion $m_g$ (nämlich $-\frac{1}{2}$ ) ein.
$\displaystyle m_d$	$=$	$\displaystyle \dfrac{-1}{-\frac{1}{2}}$
	↓	Vereinfache die rechte Seite.
$\displaystyle m_d$	$=$	$\displaystyle -2$

Stelle nun die Geradengleichung auf.

Es wird ein Punkt T, der auf der Geraden liegt benötigt. Verwendet wird der y-Abschnitt von $h\left(x\right)$ : $\left(0\vert-3\right)$ .

Setze $T\left(0\vert -3\right)$ (siehe Skizze) und $m_d$ in die allgemeine Geradengleichung ein um t zu bestimmen.

$\displaystyle -3$	$=$	$\displaystyle 2\cdot\left(0\right)+t$
	↓	Multipliziere aus .
$\displaystyle t$	$=$	$\displaystyle -3$
	↓	Setze t und $m_d$ in die allgemeine Geradengleichung ein.
$\displaystyle y$	$=$	$\displaystyle 2x-3$

Bestimme den Schnittpunkt von d und g

Berechne zunächst die x-Koordinate des Schnittpunkts S.

Normale d: $y=2x-3$

Gerade g: $y=-\frac12x+2$

Setze die Funktionen gleich.

$\displaystyle 2x-3$	$=$	$\displaystyle -\frac{1}{2}x+2$	$\displaystyle +3$
$\displaystyle 2x$	$=$	$\displaystyle -\frac{1}{2}x+5$	$\displaystyle +\frac{1}{2}x$
$\displaystyle \frac{5}{2}x$	$=$	$\displaystyle 5$	$\displaystyle :\frac{5}{2}$
$\displaystyle x$	$=$	$\displaystyle 2$

Berechne nun die y-Koordinate des Schnittpunkts S.

$\displaystyle y$	$=$	$\displaystyle 2x-3$
	↓	Setze das gefundene x = 2 ein.
$\displaystyle y$	$=$	$\displaystyle 2\cdot2-3$
	↓	Rechne aus.
$\displaystyle y$	$=$	$\displaystyle 1$

Gib die Koordinaten des Schnittpunktes S an.

$\;\;\Rightarrow\;\;$ $S\left(2\vert1\right)$

Bestimme den Abstand der Punkte S und T.

Bestimme den Abstand in x-Richtung.

$T\left(0\vert-3\right)$ , $S\left(2\vert1\right)$

Berechne die Differenz der x-Werte von S und T.

$\operatorname{\Delta}x=2-0=2$

Bestimme den Abstand in y-Richtung.

$T\left(0\vert-3\right)$ , $S\left(2\vert1\right)$

Berechne die Differenz der y-Werte.

$\operatorname{\Delta}y=1-(-3)=4$

Bestimme den Abstand in direkter Linie zwischen den Punkten.

$\operatorname{\Delta}x=2$

$\operatorname{\Delta}y=4$

Wende den Satz des Pythagoras an.

$\displaystyle d^2$	$=$	$\displaystyle 2^2+4^2$
	↓	Berechne die beiden Potenzen.
$\displaystyle d^2$	$=$	$\displaystyle 4+16$
	↓	Addiere.
$\displaystyle d^2$	$=$	$\displaystyle 20$
	↓	Ziehe die Wurzel.
$\displaystyle d$	$=$	$\displaystyle \sqrt{20}$

Wenn du $\sqrt{20}$ in den Taschenrechner eingibst und das Ergebnis auf zwei Stellen nach dem Komma rundest, erhältst du:

$d=\sqrt{20}\approx4{,}47$

Ergebnis

Der Abstand der beiden Geraden beträgt etwa 4,47.

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

Gegeben ist die Gleichung $y=\frac{3}{2}x+1$ .

Zeichne die Gerade zu der Gleichung in ein Koordinatensystem.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Wähle einen beliebigen Punkt auf der Geraden, z. B. den gegebenen y-Abschnitt $(0|1)$ , und gehe entsprechen der Steigung $m=\frac32$ zwei nach rechts und drei nach oben. Verbinde die beiden Punkte zu einer Geraden.
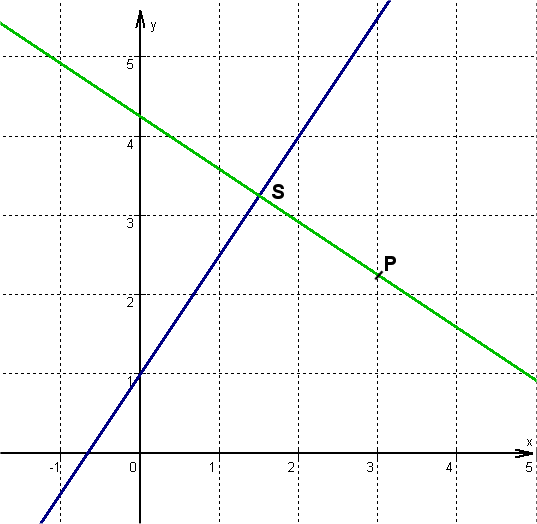
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Stelle die Gleichung der dazu senkrechten Geraden durch den Punkt $P(3|2{,}25)$ auf.

Zeichne die Gerade in dasselbe Koordinatensystem wie die Gerade aus Teilaufgabe 1.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
Wähle einen beliebigen Punkt auf der Geraden z. B. den gegebenen Punkt $P(3|2{,}25)$ und gehe entsprechen der Steigung $m=-\frac23$ , $3$ nach links und $2$ nach oben. Verbinde die beiden Punkte zu einer Geraden. (siehe Zeichnung bei Teilaufgabe 1)
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Berechne den Schnittpunkt der beiden Geraden.

Gib das Ergebnis wie folgt an: S(x|y)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle m$	$=$	$\displaystyle -1:\frac{3}{2}=\frac{-1}{1}\cdot \frac{2}{3}=-\frac{2}{3}$
	↓	Setze die Koordinaten von P und m in die allgemeine Geradengleichung ein.
$\displaystyle 2{,}25$	$=$	$\displaystyle -\frac{2}{3}\cdot3+t$
	$=$	$\displaystyle -\frac{6}{3}+t$
	$=$	$\displaystyle -\frac{2}{1}+t$
	$=$	$\displaystyle -2+t$	$\displaystyle +2$
	↓	Löse nach t auf.
$\displaystyle t$	$=$	$\displaystyle 2{,}25+2=4{,}25$

$\displaystyle \frac{3}{2}x+1$	$=$	$\displaystyle -\frac{2}{3}x+\frac{17}{4}$	$\displaystyle +\frac{2}{3}x\|-1$
	↓	Bringe alle x auf eine Seite.
$\displaystyle \frac{3}{2}x+\frac{2}{3}x$	$=$	$\displaystyle \frac{17}{4}-1$
	↓	Klammere x aus und addiere die Brüche.
$\displaystyle \frac{13}{6}x$	$=$	$\displaystyle \frac{13}{4}$	$\displaystyle :\frac{13}{6}$
$\displaystyle x$	$=$	$\displaystyle \frac{6}{4}=\frac{3}{2}=1{,}5$

Aufgaben zu parallelen und senkrechten Geraden, Abständen u. a.

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Geradengleichung aufstellen

Hast du eine Frage oder Feedback?

Gleichung aufstellen

Hast du eine Frage oder Feedback?

Gleichung aufstellen

Hast du eine Frage oder Feedback?

Gleichung aufstellen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Geradensteigung und Geradengleichung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Abstand zweier paralleler Geraden

Skizze

Geradengleichung

Bestimme den Schnittpunkt von d und g

Bestimme den Abstand der Punkte S und T.

Ergebnis

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

x-Koordinate berechnen

$y$ -Koordinate berechnen

Hast du eine Frage oder Feedback?

$\displaystyle 0$	$=$	$\displaystyle 3\cdot1+t$	$\displaystyle {-3}$
	↓	Gleichung nach t auflösen.
$\displaystyle t$	$=$	$\displaystyle -3$

$\displaystyle 2$	$=$	$\displaystyle 1+t$	$\displaystyle −1$
	↓	Gleichung nach t auflösen.
$\displaystyle t$	$=$	$\displaystyle 1$

$\displaystyle 18$	$=$	$\displaystyle 4\cdot5+t$	$\displaystyle -20$
	↓	Gleichung nach t auflösen.
$\displaystyle t$	$=$	$\displaystyle -2$

$\displaystyle 4$	$=$	$\displaystyle −2⋅(−1)+t$	$\displaystyle -2$
	↓	Gleichung nach t auflösen.
$\displaystyle t$	$=$	$\displaystyle 2$

$\displaystyle y$	$=$	$\displaystyle \frac{3}{2}\cdot \frac{3}{2}+1$
	$=$	$\displaystyle \frac{9}{4}+1$
	$=$	$\displaystyle 3{,}25$

Aufgaben zu parallelen und senkrechten Geraden, Abständen u. a.

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Geradengleichung aufstellen

Hast du eine Frage oder Feedback?

Gleichung aufstellen

Hast du eine Frage oder Feedback?

Gleichung aufstellen

Hast du eine Frage oder Feedback?

Gleichung aufstellen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Geradensteigung und Geradengleichung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Abstand zweier paralleler Geraden

Skizze

Geradengleichung

Bestimme den Schnittpunkt von d und g

Bestimme den Abstand der Punkte S und T.

Ergebnis

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

x-Koordinate berechnen

yyy-Koordinate berechnen

Hast du eine Frage oder Feedback?

$y$ -Koordinate berechnen