Aufgaben zu linearen Funktionen

Berechne den Abstand der Geraden zum Ursprung.

$y = \frac{3}{4} x - 5$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung der Senkrechten
Geradensteigung und Geradengleichung
Der kürzeste Abstand zum Ursprung ist die Senkrechte auf die Gerade durch den Ursprung. Ist $g (x) : y = m_{1} \cdot x + b$ , so berechnest du die Steigung der Senkrechten $m_{2}$ mit der Formel.
$m_{2} = - \frac{1}{m_{1}}$
Setz den Wert der Steigung ein.
$m_{2} = - \frac{1}{\frac{3}{4}} = - \frac{4}{3}$
Die gesuchte Senkrechte hat also Steigung $- \frac{4}{3}$ und geht durch den Ursprung, der y-Achsenabschnitt $b$ ist also 0. Damit lautet die Geradengleichung der Senkrechte $h (x) : y = - \frac{4}{3} x$ .
Berechne nun den Schnittpunkt $A (x_{s} | y_{s})$ der beiden Geraden indem du ihre Geradengleichungen gleichsetzt.
$g (x_{s})$ $=$ $h (x_{s})$
↓
Setz die Geradengleichungen ein.
$- \frac{4}{3} x_{s}$ $=$ $\frac{3}{4} x_{s} - 5$ $- \frac{3}{4} x_{s}$
↓
Bringe die Variable $x_{s}$ auf die linke Seite.
$- \frac{25}{12} x_{s}$ $=$ $- 5$ $\cdot (- 1)$
$\frac{25}{12} x_{s}$ $=$ $5$ $: \frac{25}{12}$
$x_{s}$ $=$ $\frac{12}{5}$
$=$ $2,4$
Setz nun $x_{s}$ in eine der Geradengleichungen ein um $y_{s}$ zu bestimmen.
$h (x_{s}) : y_{s} = - \frac{4}{3} x_{s}$
Setz $x_{s} = 2,4$ ein.
$y_{s} = - \frac{4}{3} \cdot 2,4 = - 3,2$
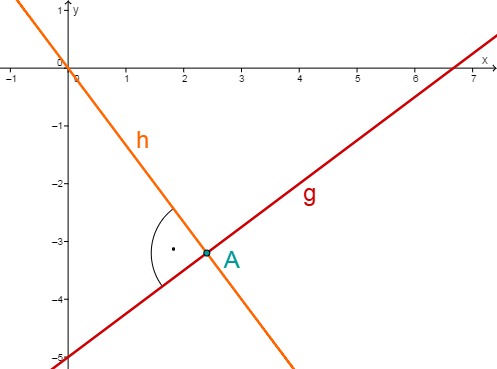
Der Schnittpunkt der Geraden $h$ und $g$ liegt also bei $A (2,4 | - 3,2)$ .
Bestimme nun den Abstand des Ursprungs zum berechneten Schnittpunkt $A$ , dies ist genau der kürzeste Abstand der Geraden $g$ zum Ursprung.
$d = \sqrt{(x_{s} - x_{0})^{2} + (y_{s} - y_{0})^{2}}$
Setz die Werte ein.
$d = \sqrt{(2,4 - 0)^{2} + (- 3,2 - 0)^{2}}$
Vereinfache.
$= \sqrt{5,76 + 10,24} = \sqrt{16} = 4$
Der kürzeste Abstand der Geraden $g$ zum Ursprung ist also 4.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
$y = - \frac{1}{2} x + 2$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
Der kürzeste Abstand zum Ursprung ist die Senkrechte auf die Gerade durch den Ursprung. Ist $g (x) : y = m_{1} \cdot x + b$ , so berechnest du die Steigung der Senkrechten $m_{2}$ mit der Formel
$m_{2} = - \frac{1}{m_{1}}$
Setz den Wert der Steigung ein.
$m_{2} = - \frac{1}{- \frac{1}{2}} = 2$
Die gesuchte Senkrechte hat also Steigung $2$ und geht durch den Ursprung, der y-Achsenabschnitt $b$ ist also 0. Damit lautet die Geradengleichung der Senkrechte $h (x) : y = 2 x$ .
Berechne nun den Schnittpunkt $A (x_{s} | y_{s})$ der beiden Geraden, indem du ihre Geradengleichungen gleichsetzt.
$g (x_{s})$ $=$ $h (x_{s})$
↓
Setz die Geradengleichungen ein.
$- \frac{1}{2} x_{s} + 2$ $=$ $2 x_{s}$ $- 2 x_{s}$
↓
Bringe die Variable $x_{s}$ auf die linke Seite.
$- 2,5 x_{s} + 2$ $=$ $0$ $- 2$
↓
Bringe die 2 auf die rechte Seite.
$- 2,5 x_{s}$ $=$ $- 2$ $: (- 2,5)$
$x_{s}$ $=$ $0,8$
Setz nun $x_{s}$ in eine der Geradengleichungen ein um $y_{s}$ zu bestimmen.
$h (x_{s}) : y_{s} = 2 x_{s}$
Setz $x_{s} = 0,8$ ein.
$y_{s} = 2 \cdot 0,8 = 1,6$
Der Schnittpunkt der Geraden $h$ und $g$ liegt also bei $A (0,8 | 1,6)$ .
Bestimme nun den Abstand des Ursprungs zum berechneten Schnittpunkt $A$ , dies ist genau der kürzeste Abstand der Geraden $g$ zum Ursprung.
$d = \sqrt{(x_{s} - x_{0})^{2} + (y_{s} - y_{0})^{2}}$
Setz die Werte ein.
$d = \sqrt{(0,8 - 0)^{2} + (1,6 - 0)^{2}}$
Vereinfache.
$= \sqrt{0,64 + 2,56} = \sqrt{3,2} \approx 1,79$
Der kürzeste Abstand der Geraden $g$ zum Ursprung ist also etwa $1,79$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$g (x_{s})$	$=$	$h (x_{s})$
	↓	Setz die Geradengleichungen ein.
$- \frac{4}{3} x_{s}$	$=$	$\frac{3}{4} x_{s} - 5$	$- \frac{3}{4} x_{s}$
	↓	Bringe die Variable $x_{s}$ auf die linke Seite.
$- \frac{25}{12} x_{s}$	$=$	$- 5$	$\cdot (- 1)$
$\frac{25}{12} x_{s}$	$=$	$5$	$: \frac{25}{12}$
$x_{s}$	$=$	$\frac{12}{5}$
	$=$	$2,4$

Geradensteigung und Geradengleichung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?