Berechne für die folgende Funktion die Nullstellen und den Funktionswert, der an der Stelle angenommen wird. Zeichne den Graphen der Funktion in ein Koordinatensystem.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
Setze die Funktion gleich 0.
Du erhältst eine quadratische Gleichung. und kannst daher mit der Mitternachtsformel arbeiten.
Berechne zunächst die Diskriminante ; denn falls ist, gibt es ohnehin keine Lösungen.
Damit besitzt keine Nullstellen.
Funktionswert an der Stelle x = 2
Setze für x den Wert 2 ein.
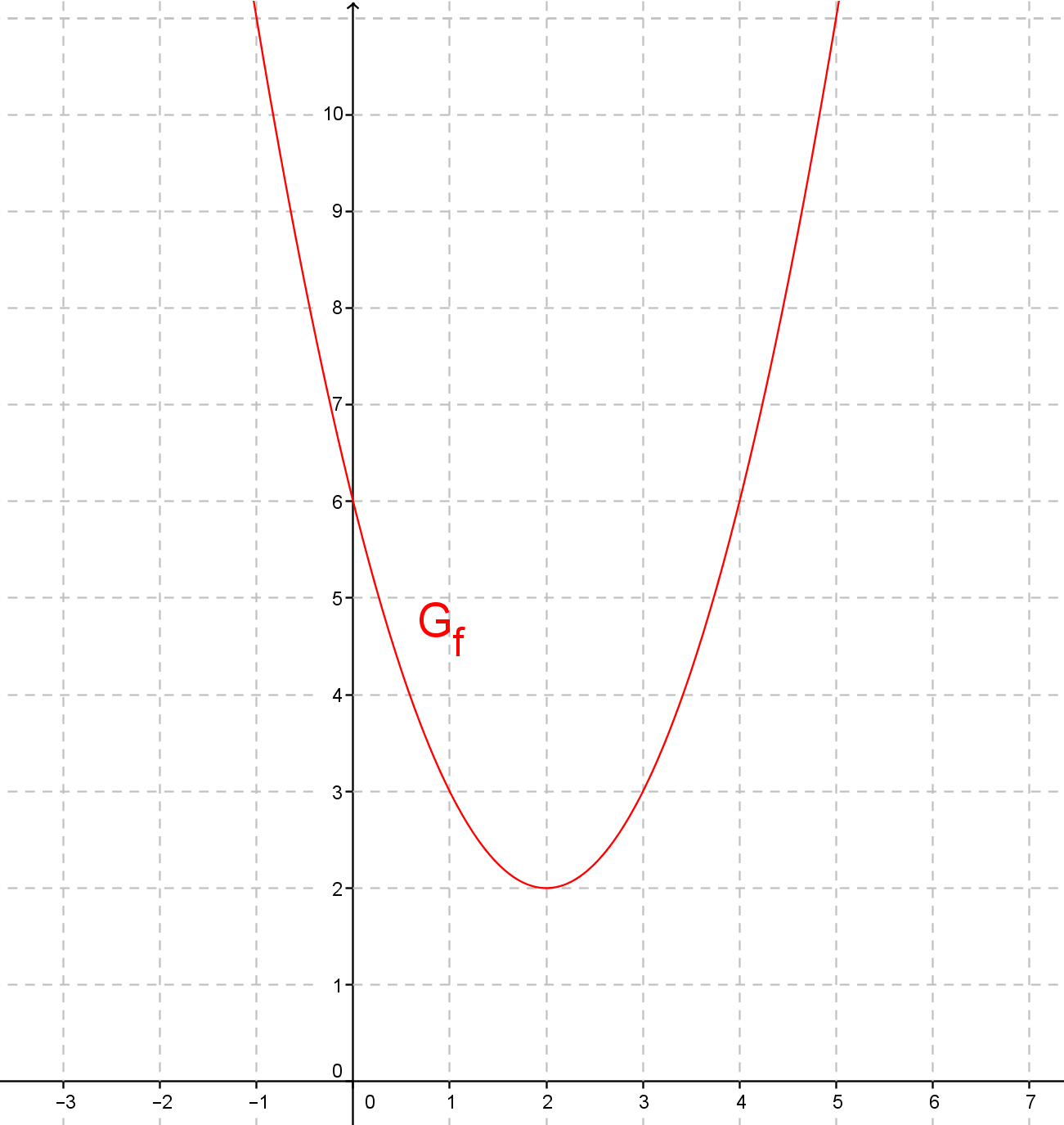
Graphen zeichnen
Um den Graphen zu zeichnen, kannst du verschieden vorgehen:
1. Möglichkeit: Scheitelform
Also handelt es sich bei um eine verschobene Normalparabel mit Scheitel .
2. Möglichkeit: Lege mit dem Taschenrechner eine Wertetabelle an.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
Setze die Funktion gleich 0.
Du erhältst eine quadratische Funktion und kannst daher mit der Mitternachtsformel arbeiten.
Berechne zunächst die Diskriminante ; denn falls ist, gibt es ohnehin keine Lösung.
Damit besitzt keine Nullstellen.
Funktionswert an der Stelle x = 2
Setze in x den Wert 2 ein.
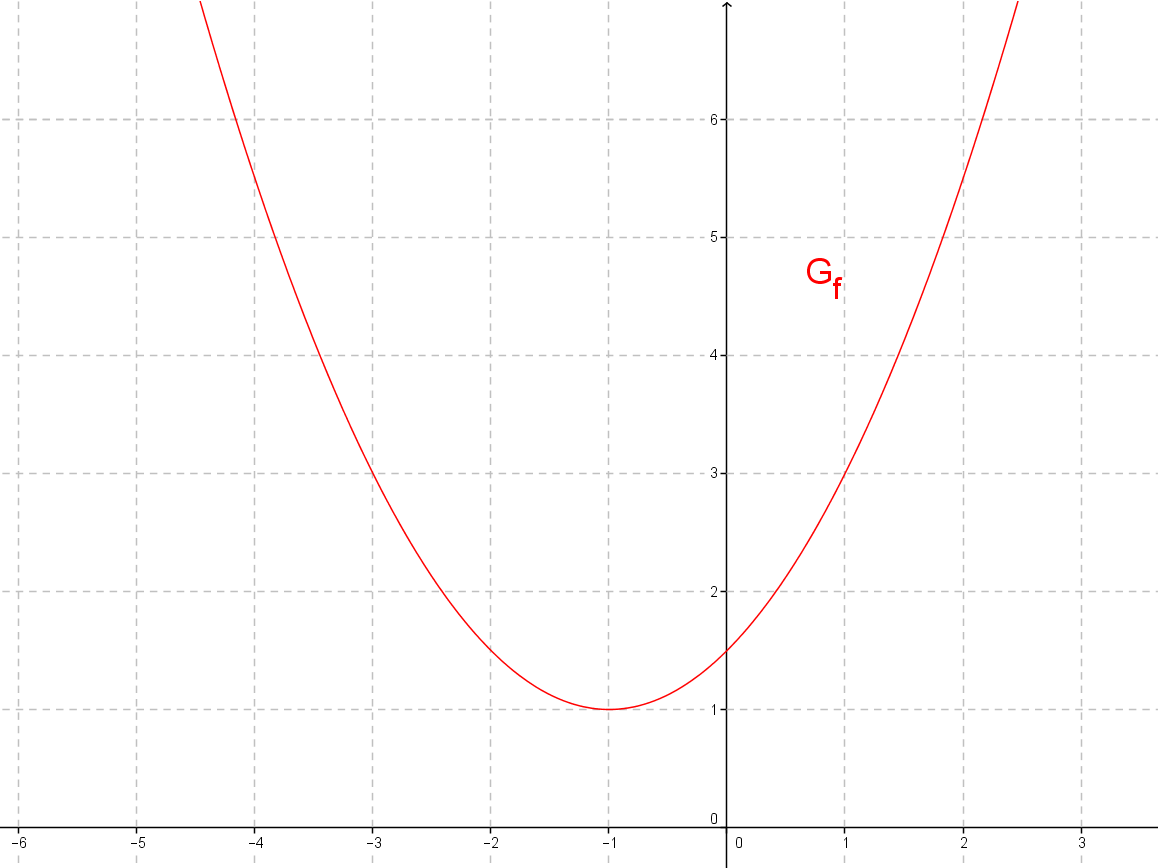
Graphen zeichnen
Um den Graphen von zu zeichnen, kannst du verschieden vorgehen.
1. Möglichkeit: Scheitelform
Damit handelt es sich bei um eine um den Faktor gestauchte Normalparabel mit Scheitel .
2. Möglichkeit:
Erstelle mit dem Taschenrechner/im Kopf eine Wertetabelle.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
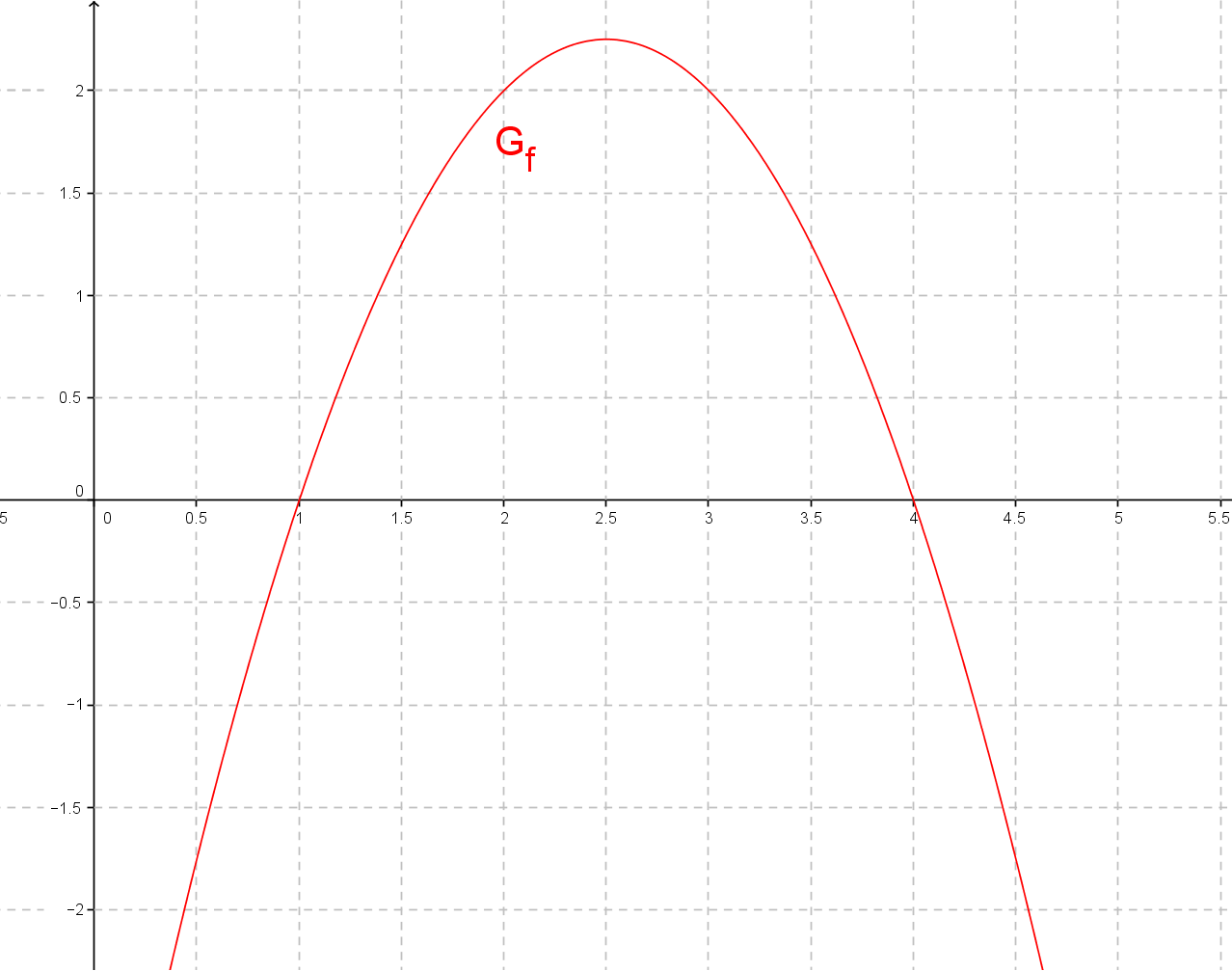
Funktion gleich 0 setzen.
Diskriminante berechnen.
Daher gibt es zwei Nullstellen.
In die Mitternachsformel einsetzen dabei die berechnete Diskriminante einsetzen.
die Nullstellen sind und .
Funktionswert an der Stelle x = 2
einsetzen.
Graphen zeichnen
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
