Aufgaben zur Addition und Subtraktion ganzer Zahlen
- 1
Führe folgende Additionen/Subtraktionen mit Hilfe einer Zahlengeraden durch:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition auf der Zahlengerade
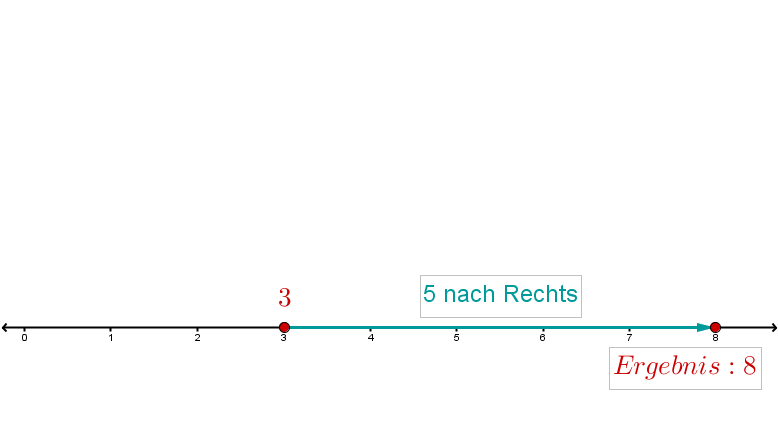
Gehe vom Nullpunkt aus Schritte nach rechts, um zu finden.
Da es sich um eine Addition handelt, gehe Schritte nach rechts.
Das Ergebnis ist .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition auf der Zahlengerade
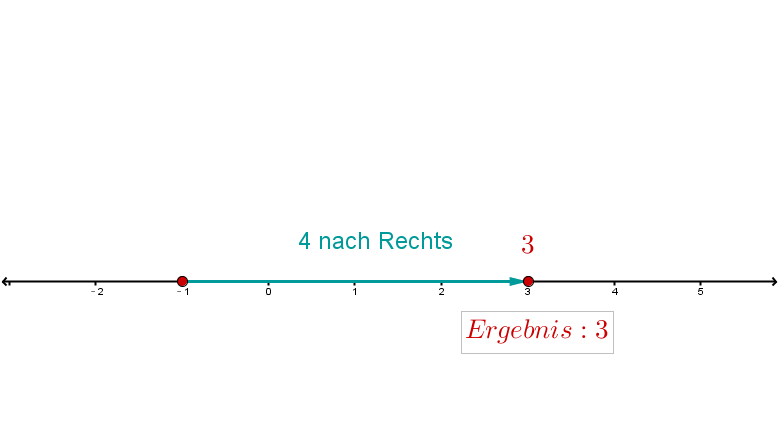
Da eine negative Zahl ist, muss man vom Nullpunkt aus einen Schritt nach links gehen, um zu finden.
Gehe Schritte nach rechts, da es sich um eine Addition handelt.
Das Ergebnis ist .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition auf der Zahlengerade
Da eine negative Zahl ist, muss man vom Nullpunkt aus Schritte nach links gehen, um zu finden.
Gehe einen Schritt nach links, da es sich um eine Subtraktion handelt.
Das Ergebnis ist .

Hast du eine Frage oder Feedback?
- 2
Berechne folgende Ausdrücke mit den Rechenregeln.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen
Lösungsweg 1
Du ziehst von einer positiven Zahl eine größere ab. Das Ergebnis ist also negativ.
Lösungsweg 2
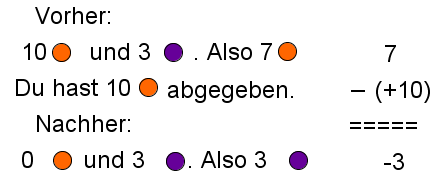
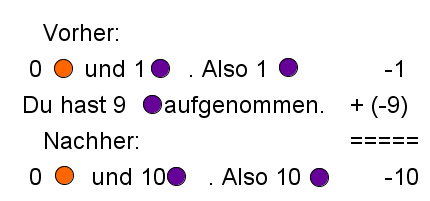
…mit dem Kontospiel: (Beide Möglichkeiten sind richtig.)
Möglichkeit 1:
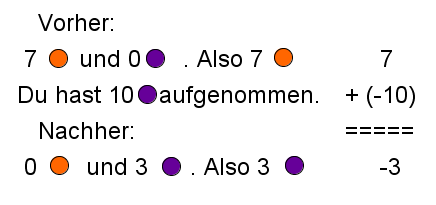
Möglichkeit 2:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen
Lösungsweg 1
Beachte: "Minus und Minus gibt Plus"
Lösungsweg 2
… mit dem Kontospiel:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen
Lösungsweg 1
In der Rechnung steht ein Minuszeichen. Bilde also die Beträge der Zahlen.
und
Ziehe vom größeren Betrag den kleineren Betrag ab.
Schreibe vor die Differenz das Vorzeichen der betragsmäßig größeren Zahl. Das ist hier die . Das Vorzeichen also ein Plus.
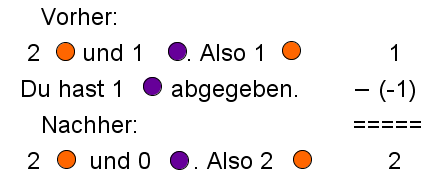
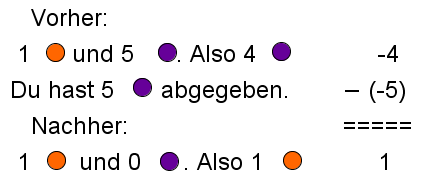
Lösungsweg 2
… mit dem Kontospiel:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen
Lösungsweg 1
Zur negativen Zahl kommen weitere hinzu.
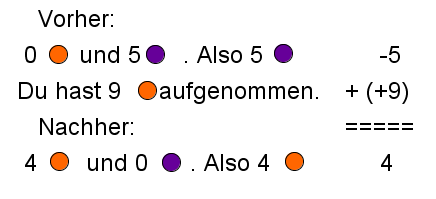
Lösungsweg 2:
… mit dem Kontospiel:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen
Lösungsweg 1
Es gilt die Regel: "Minus und Minus ergibt Plus"
Zur negativen Zahl wird eine positive Zahl mit größerem Betrag addiert. Das Ergebnis ist also positiv.
Lösungsweg 2
…mit dem Kontospiel:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtrakiton ganzer Zahlen
Von der negativen Zahl werden weitere abgezogen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen
Aus Minus und Minus wird Plus.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen
Hast du eine Frage oder Feedback?
- 3
Berechne folgende Terme! (Rechenausdrücke)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Klammern auflösen
Löse die Klammer auf.
Addiere die positiven Summanden.
Subtrahiere.
Hast du eine Frage oder Feedback?
- 4
Was ist die Lösung der Differenz ?
Begründe ohne Rechnung.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen
Eine Überschlagsrechnung ergibt:
Damit kommen nur noch oder als mögliche Lösungen in Frage.
Die Betrachtung der letzten Ziffern ergibt: . Damit muss auch die letzte Ziffer der Lösung eine sein.
Also ist das korrekte Ergebnis.
- 5
Subtrahiere von der kleinsten ungeraden dreistelligen Zahl die Summe der vier größten zweistelligen Zahlen.
Du kannst dein Ergebnis im Eingabefeld überprüfen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Grundrechenarten
Zahlen bestimmen
Kleinste ungerade dreistellige Zahl:
Vier größten zweistelligen Zahlen:
Wert des Terms berechnen
↓ In der Klammer addieren .
↓
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?