Ein Werkstück besteht aus einem Halbzylinder und einer quadratischen Pyramide ( = 16 cm ; = 20 cm).
Berechne das Volumen des Werkstücks. (4 Punkte)
Hinweis: Die Skizze ist nicht maßstabgetreu.
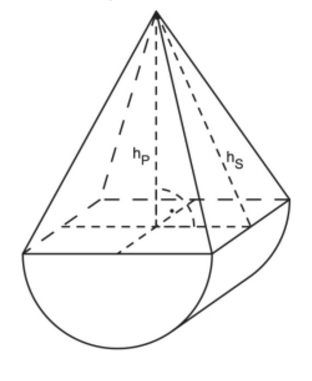
Ein Werkstück besteht aus einem Halbzylinder und einer quadratischen Pyramide ( = 16 cm ; = 20 cm).
Berechne das Volumen des Werkstücks. (4 Punkte)
Hinweis: Die Skizze ist nicht maßstabgetreu.
