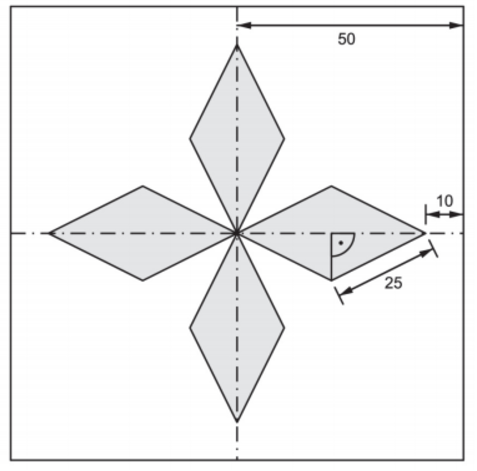
In einer Fensterscheibe sind vier gleiche, farbige Glasscheiben eingesetzt. Sie haben jeweils die Form einer Raute (siehe Abbildung). Berechne die Gesamtfläche des farbigen Glases. (4 Punkte)
Hinweis: Skizze nicht Maßstabgetreu.
Maße in cm.
cm²
In einer Fensterscheibe sind vier gleiche, farbige Glasscheiben eingesetzt. Sie haben jeweils die Form einer Raute (siehe Abbildung). Berechne die Gesamtfläche des farbigen Glases. (4 Punkte)
Hinweis: Skizze nicht Maßstabgetreu.
Maße in cm.
