Teil B, Gruppe 3

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Löse folgende Gleichung. (4 Punkte)
$\frac{1}{8} \cdot (2 x + 6) = \frac{1}{2} - 2 x + 2 + \frac{3 x + 8}{4}$
=x

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lösen von linearen Gleichungen
Videolösung
Textlösung
Für diese Aufgabe brauchst du das Lösen von linearen Gleichung und die Addition und Multiplikation von Brüchen.
$\frac{1}{8} \cdot 2 x + \frac{1}{8} \cdot 6 = \frac{1}{2} - 2 x + 2 + \frac{3 x + 8}{4}$
Fasse die linke Seite soweit wie möglich zusammen. Multipliziere hierzu auf der linken Seite der Gleichung den Bruch $\frac{1}{8}$ mit dem jeweiligen Faktor. Kürze dabei den entstandenen Bruch auch so weit wie möglich!
$\frac{1}{4} x + \frac{3}{4} = \frac{1}{2} - 2 x + 2 + \frac{3 x + 8}{4}$
Löse den Bruch rechts auf, indem du $3 x$ und $8$ durch $4$ teilst. Anschließend teilst du den Bruch in $\frac{3 x}{8}$ und $\frac{8}{4} = 2$ auf.
$\frac{1}{4} x + \frac{3}{4} = \frac{1}{2} - 2 x + 2 + \frac{3 x}{4} + 2$
Vereinfache beide Seiten, indem du die Zahlen zusammenfasst und alles was von $x$ abhängig ist.
Zusätzlich kannst du, um schöner weiterzurechnen, alles in Dezimalzahlen umformen.
$0,25 x + 0,75 = 4,5 - 1,25 x | + 1,25 x$
Addiere als nächstes $1,25 x$ auf beiden Seiten.
$1,5 x + 0,75 = 4,5 | - 0,75$
Subtrahiere anschließend auf beiden Seiten $0,75$ .
$1,5 x = 3,75 | : (1,5)$
Teile auf beiden Seiten durch $1,5$ .
$x = 2,5$
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
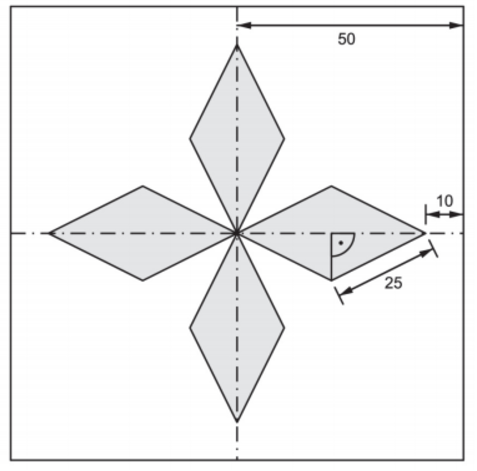
In einer Fensterscheibe sind vier gleiche, farbige Glasscheiben eingesetzt. Sie haben jeweils die Form einer Raute (siehe Abbildung). Berechne die Gesamtfläche des farbigen Glases. (4 Punkte)
Hinweis: Skizze nicht Maßstabgetreu.
Maße in cm.
cm²

Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt eines Dreiecks
Um die Gesamtfläche des farbigen Glases zu berechnen, kannst du sie zuerst in vier gleiche Rauten aufteilen. Den Flächeninhalt dieser Rauten kannst du wiederum als vier kongruente, rechtwinklige Dreiecke berechnen, die entstehen, wenn du bei der Raute die Diagonalen einzeichnest.
Die kleinen kongruenten, rechtwinkligen Dreiecke werden während dem Rechnen als Dreieck $Δ$ bezeichnet.
Berechnung der längeren Kathete von Dreieck $Δ$
Um den Flächeninhalt von Dreiecken $Δ$ zu berechnen, werden die Längen von beiden Katheten des Dreiecks benötigt, da diese als Höhe und Breite des Dreiecks verwendet werden können.
Die längere Kathete kannst du berechnen, indem du zuerst die 10 cm lange Strecke von der 50 cm langen Hälfte der Seite des gesamten, quadratischen Spiegels subtrahierst. Dadurch erhältst du die längere Diagonale der Raute.
$50 cm - 10 cm = 40 cm$
Du teilst nun die längere Diagonale der Raute durch zwei, um die längere Kathete von Dreieck $Δ$ zu erhalten
$40 cm : 2 = 20 cm$
Berechnung der kürzeren Kathete von Dreieck $Δ$
Du kannst nun den Satz des Pythagoras anwenden, um die zweite, kürzere Kathete von Dreieck $Δ$ zu berechnen. Du kennst die Länge der ersten Kathete (20 cm) und der Hypotenuse (25cm), da die Hypotenuse gleichzeitig auch die Seite von einer der Rauten ist, von der die Länge schon in der Skizze angegeben ist.
$x^{²} {cm}^{2} + 20^{2} {cm}^{2} = 25^{2} {cm}^{2}$
Von beiden Seiten der Gleichung subtrahierst du $20^{2} {cm}^{2}$ .
$x^{²} {cm}^{2} = 25^{2} {cm}^{2} - 20^{2} {cm}^{2}$
Ziehe die Wurzel nun auf beiden Seiten der Gleichung.
$x cm = \sqrt{25^{2} {cm}^{2} - 20^{2} {cm}^{2}}$
$x cm = \sqrt{625 {cm}^{2} - 400 {cm}^{2}}$
$x cm = \sqrt{225 {cm}^{2}}$
$x cm = 15 cm$
Da nun beide Kathetenlängen, bzw. die Höhe und die Breite bekannt sind, kannst du nun den Flächeninhalt von Dreieck $Δ$ bestimmen.
$A_{Δ} = \frac{1}{2} \cdot 20 cm \cdot 15 cm = 150 {cm}^{2}$
Du erhältst die Gesamtfläche des farbigen Glases, wenn du den gerade eben bestimmten Flächeninhalt von Dreieck $Δ$ mit 16 multiplizierst, da die Gesamtfläche aus vier kongruenten Rauten besteht, welche sich wiederum jeweils aus vier kongruenten Dreiecken zusammensetzen.
$A_{gesamt} = 4 \cdot 4 \cdot A_{Δ} = 16 \cdot A_{Δ}$
$= 16 \cdot 150 {cm}^{2}$
$= 2400 {cm}^{2}$
Die Gesamtfläche des farbigen Glases $A_{gesamt}$ ist $2400 {cm}^{2}$ groß.
Videoerklärung
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
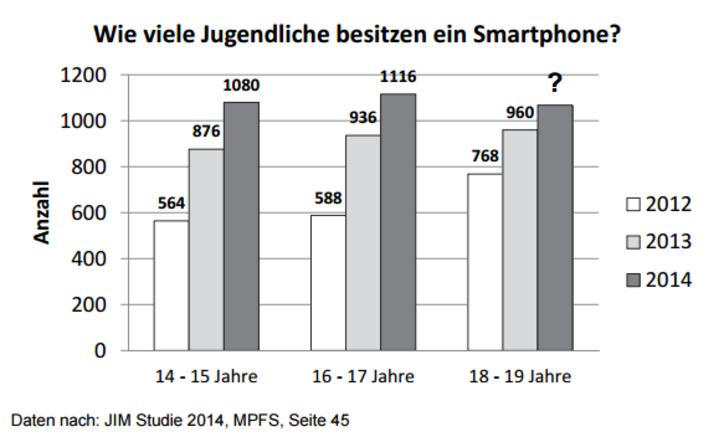
In den Jahren 2012 bis 2014 wurden in jeder Altersgruppe jeweils 1200 Jugendliche befragt, ob sie ein Smartphone besitzen. (4 Punkte)
1. Berechne den prozentualen Anstieg der Smartphone-Besitzer von 2012 auf 2014 in der Altersgruppe der 14- bis 15-Jährigen.
  % beträgt der Anstieg.
  
  Videolösung
  Lösung zur Teilaufgabe a)
  Für diese Teilaufgabe solltest du Prozentrechnung mittels Dreisatz beherrschen.
  Berechne, wie viel mehr Jugendliche im Jahr 2014 ein Smartphone besaßen als im Jahr 2012.
  $1080 - 564 = 516$
  Berechne, wie viel Prozent $516$ von $564$ sind. Teile dafür zunächst $516$ durch $564$ .
  $516 : 564 = 0,91489..$
  Nehme dein Ergebnis mit $100$ mal, um zu erfahren, wie viele Prozent das sind.
  $0,91489 \cdot 100 = 91,49 %$ $\Rightarrow$ Der Anteil der Jugendlichen, die ein Smartphone besitzen, ist von 2012 bis 2014 um $91,49 %$ gestiegen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. In der Altersgruppe der 18- und 19-Jährigen stieg die Anzahl der Smartphone-Besitzer von 2013 auf 2014 um $11,25$ %. Ermittle rechnerisch, wie viele Jugendliche dieser Altersgruppe demnach 2014 ein Smartphone besaßen.
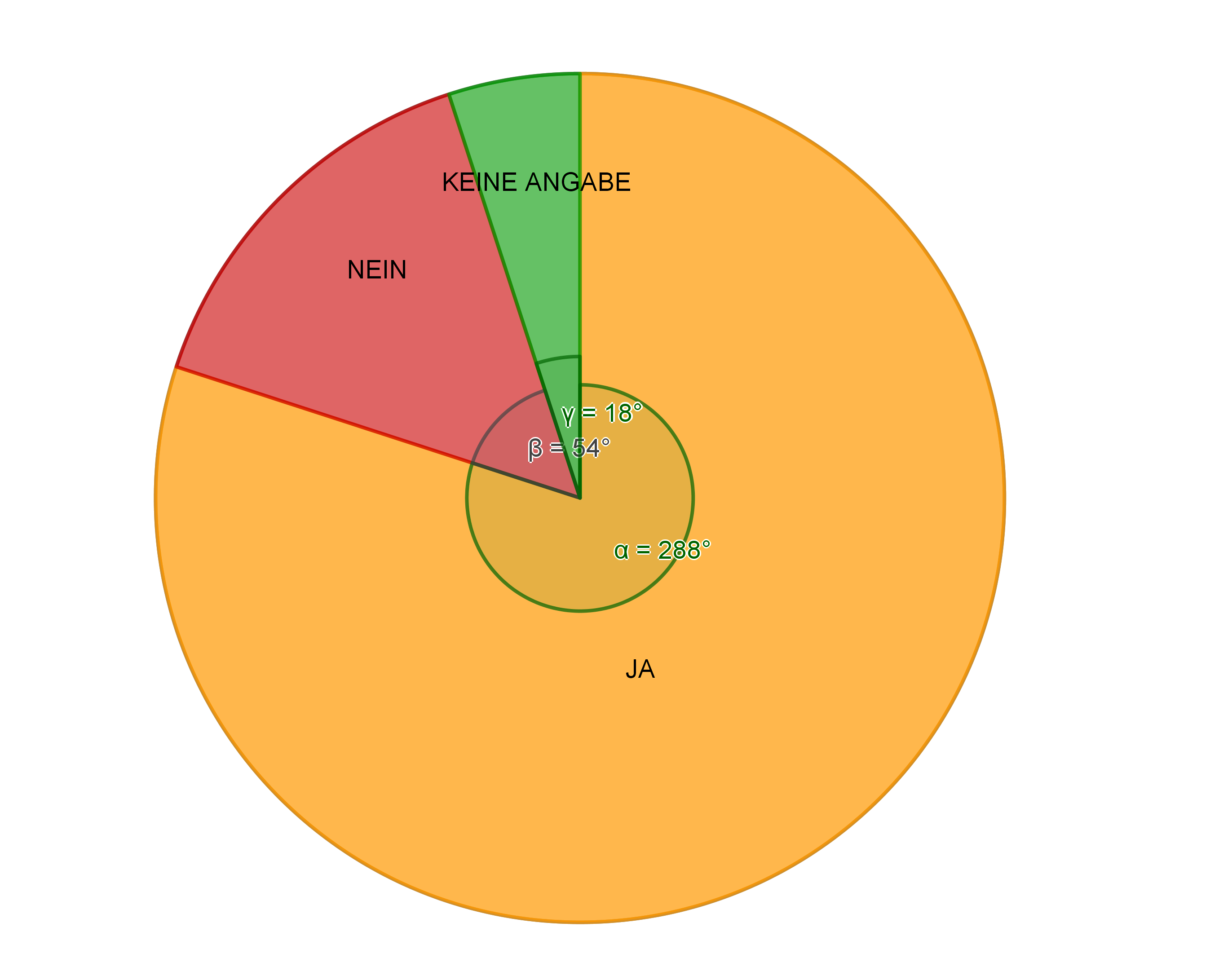
  Jugendliche
  
  Videolösung
  Lösung zur Teilaufgabe b)
  Auch für diese Teilaufgabe solltest du Prozentrechnung mittels Dreisatz beherrschen.
  Berechne, wie viele Jugendliche einem Prozent entsprechen, indem du die Anzahl 2013 ( $960$ ) durch $100$ teilst.
  $960 : 100 = 9,6$
  Ein Prozent sind also $9,6$ Jugendliche. Multipliziere dies mit der Gesamtprozentzahl: Grundsätzlich sind 2013 $100 %$ Jugendliche Smartphonebesitzer und 2014 sind es $11,25 %$ mehr, also sind es insgesamt $100 % + 11,25 % = 111,25 %$ .
  Multipliziere also $9,6$ mit $111,25$ :
  $9,6 \cdot 111,25 = 1068$
  $\Rightarrow$ Im Jahr 2014 nutzen $1068$ 18- bis 19- jährige ein Smartphone.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Im Jahr 2014 wurden zusätzlich $1200$ Jugendliche im Alter zwischen 12 und 13 Jahren befragt. $80$ % besaßen ein Smartphone, $15$ % besaßen keines, der Rest machte keine Angabe. Stelle das Ergebnis dieser Umfrage in einem Kreisdiagramm mit Radius 4cm dar.
  °
  
  Videolösung
  Lösung zur Teilaufgabe c)
  Für diese Teilaufgabe solltest du ein Kreisdiagramm zeichnen können, außerdem brauchst du wieder die Prozentrechnung mittels Dreisatz.
  Berechne die Winkel für die jeweilige Antwort. Berechne, wie groß der Winkel für $1 %$ ist, indem du den Vollwinkel $360 °$ durch $100$ teilst.
  $360 ° : 100 = 3,6 °$
  Ein Prozent ist also ein Winkel von $3,6 °$ . Multipliziere die Prozentangaben aus der Aufgabe mit $3,6 °$ .
  Ja $\Rightarrow$ $3,6 ° \cdot 80 = 288 °$ Nein $\Rightarrow$ $3,6 ° \cdot 15 = 54 °$
  Berechne die Prozentzahl bei keine Angabe.
  Keine Angabe $\Rightarrow$ $100 - 80 - 15 = 5$
  Multipliziere die berechnete Prozentangaben mit $3,6 °$ .
  $3,6 ° \cdot 5 = 18 °$
  Zeichne einen Kreis mit dem Radius 4cm. Trage die oben berechneten Winkel ein.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Löse die folgenden Aufgaben. [4 Punkte]
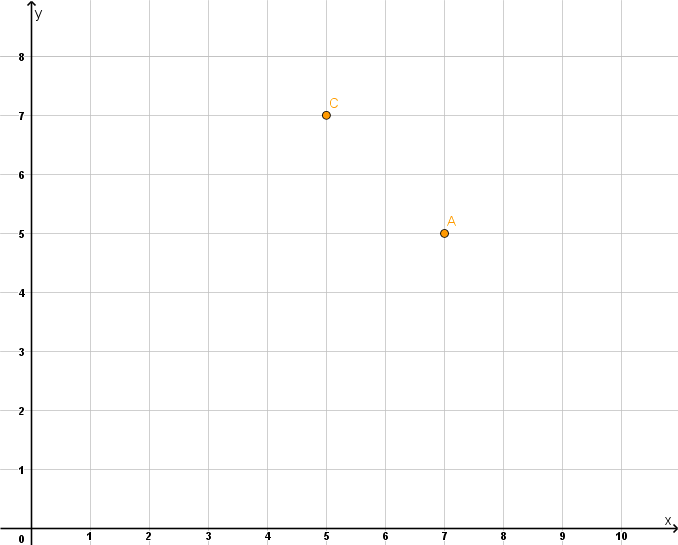
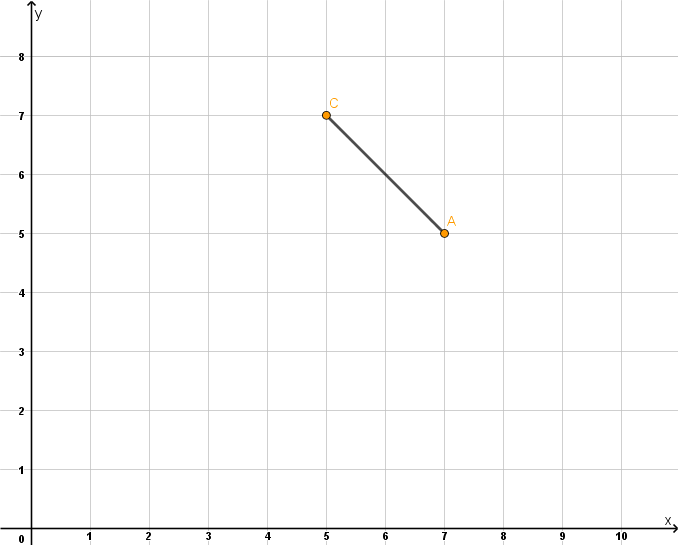
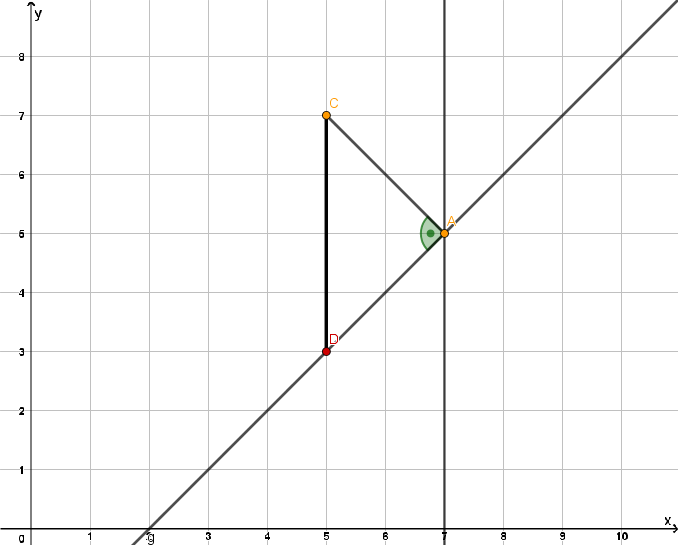
1. Zeichne in ein Koordinatensystem mit der Einheit 1cm die Punkte $A (7 | 5)$ und $C (5 | 7)$ ein und verbinde sie zur Strecke [AC].
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
  Für diese Teilaufgabe benötigst du das Zeichnen eines Koordinatensystems mit dem Einzeichnen von Punkten.
  Verbinde die Punkte A und C zu einer Strecke.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
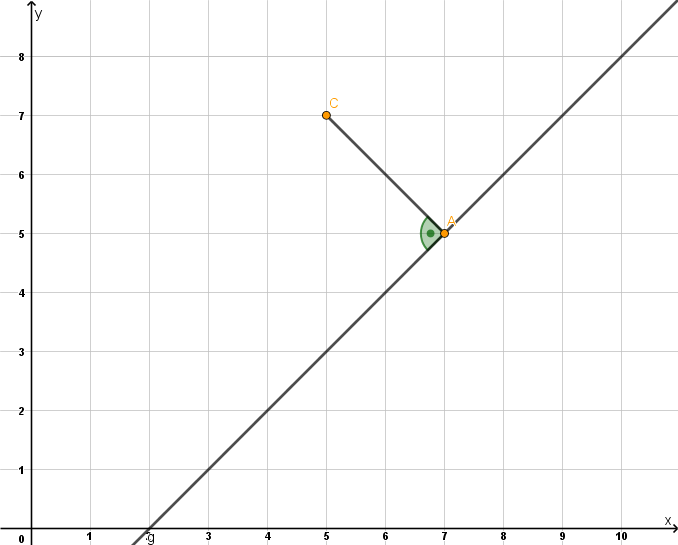
2. Zeichne die Senkrechte zur Strecke [AC] durch den Punkt A.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
  Zeichne eine Senkrechte zur Strecke AC, die durch den Punkt A läuft.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
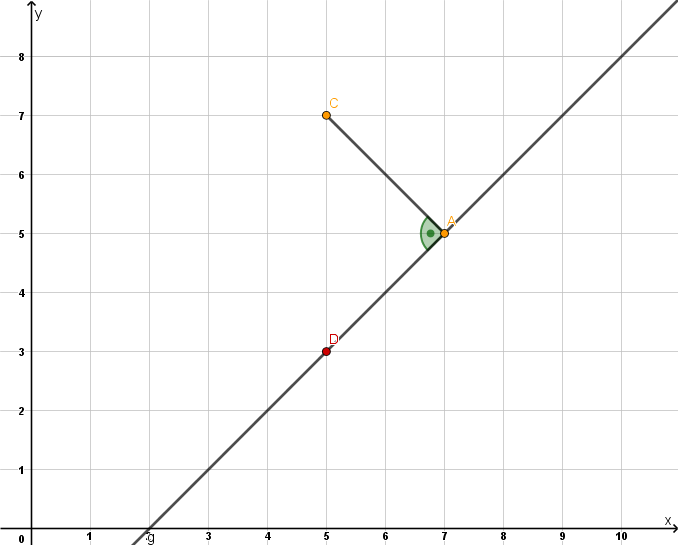
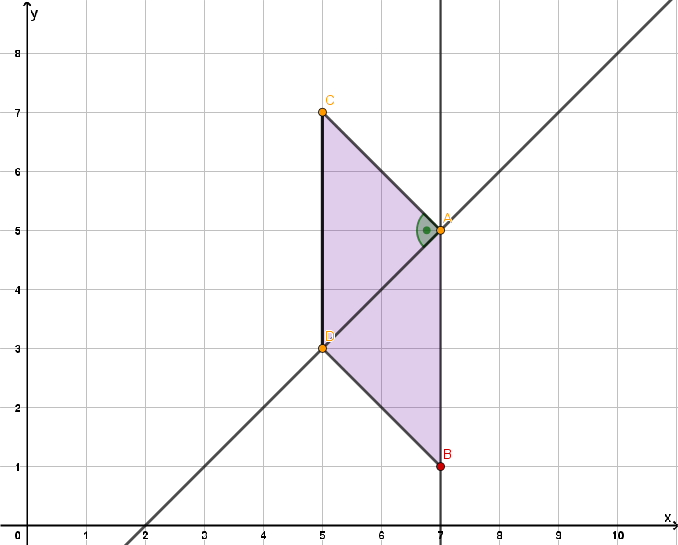
3. Zeichne den Punkt $D (5 | 3)$ ein. Wähle den Punkt B so, dass das Parallelogramm $A B C D$ entsteht und zeichne es.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
  Zeichne den Punkt D bei $(5 | 3)$ .
  Zeichne die Strecke CD.
  Zeichne eine Parallele zur Strecke CD durch den Punkt A.
  Zeichne ebenso eine Parallele zur Strecke AC durch den Punkt D. An der Stelle wo sich die beiden Geraden kreuzen, ist der gesuchte Punkt B. Zeichne ihn ein und du erhälst ein Parallelogramm.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
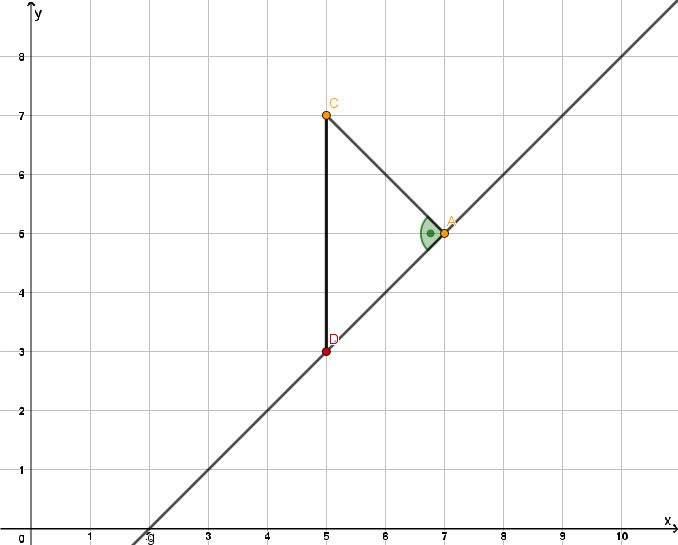
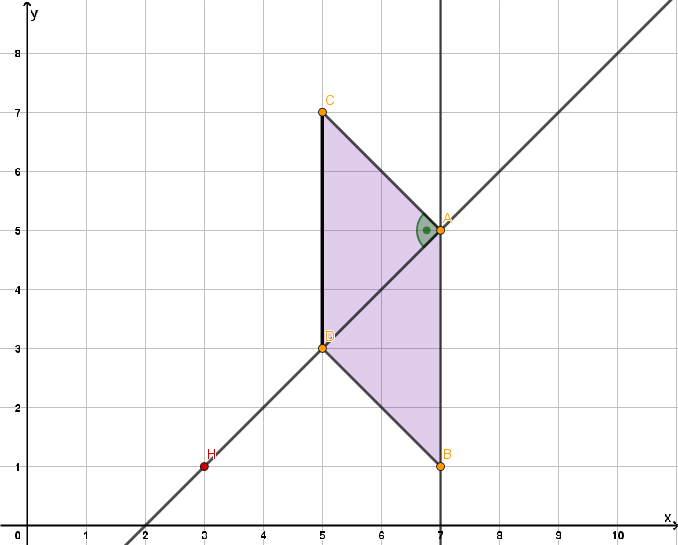
4. Der Punkt D soll die Strecke [AH] halbieren. Zeichne den Punkt H entsprechend ein und gib seine Koordinaten an.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
  Messe die Strecke AD und übertrage sie auf die gegenüberliegende Seite von D. Der Punkt, der von D gleich weit entfernt ist, wie der Punkt A, ist dein neuer Punkt H.
  Der Punkt $H$ liegt bei $(3 | 1)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉