Umrechnen von Brüchen in Dezimalzahlen

Es gibt zwei Methoden, einen Bruch in eine Dezimalzahl umzuwandeln:

durch Erweitern bzw. Kürzen
durch schriftliches Dividieren

Vergleich der Methoden

	Erweitern bzw. Kürzen	Schriftliches Dividieren
Vorteil	meist schneller	funktioniert immer
Nachteil	funktioniert nur bei Brüchen, die auf 10er, 100er, 1000er im Nenner erweiter- oder kürzbar sind	oft zeitaufwändiger

Umrechnung durch Erweitern bzw. Kürzen

Durch Erweitern oder Kürzen lassen sich Brüche in Dezimalzahlen umwandeln

Bruch mit Zehnerpotenz im Nenner

Wenn ein Bruch eine Zehnerpotenz ( $10, 100, 1000,…$ ) im Nenner hat, ist es ganz einfach, ihn als Dezimalzahl zu schreiben.

Beispiel

Schreibe den Bruch als Summe.
Kürze die Summanden so.

Zerlege den Zähler.
	↓
$\displaystyle \frac{2375}{1000}$	$=$	$\displaystyle \frac{2000+300+70+5}{1000}$
	↓	Schreibe den Bruch als Summe.
	$=$	$\displaystyle \frac{2000}{1000}+\frac{300}{1000}+\frac{70}{1000}+\frac{5}{1000}$
	↓	Kürze die Brüche.
	$=$	$\displaystyle \frac{2}{1}+\frac{3}{10}+\frac{7}{100}+\frac{5}{1000}$

Schließlich kann man die Werte so in die Stellenwerttabelle eintragen:

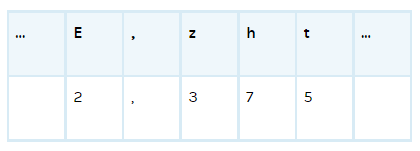
Wir erhalten: $\dfrac{2375}{1000} = 2{,}375$

Bruch mit beliebigem Nenner

Wenn im Nenner keine Zehnerpotenz steht, kann man manche Brüche so erweitern oder kürzen, dass man eine Zehnerpotenz erhält.

Beachte

Beim Erweitern funktioniert das nur, wenn im Nenner ein Produkt aus den Zahlen 2 und/oder 5 steht.

Beispiele für Nenner:

$4=2\cdot2$

$125=5\cdot5\cdot5$

$20=2\cdot2\cdot5$

Beispiel

Überprüfe, ob der Nenner ein Produkt aus $2$ und/oder $5$ ist.
Erweitere so, dass eine Zehnerpotenz im Nenner steht.

$\frac{19}{8}\rightarrow 8=2\cdot 2\cdot 2$

$\displaystyle \frac{19}{8}$	$=$	$\displaystyle \frac{19\ \cdot5\cdot5\cdot5}{2\cdot2\cdot2\cdot5\cdot5\cdot5}$
	$=$	$\displaystyle \frac{19\cdot125}{\left(2\cdot5\right)\cdot\left(2\cdot5\right)\cdot\left(2\cdot5\right)}$
	$=$	$\displaystyle \frac{2375}{10\cdot10\cdot10}$
	$=$	$\displaystyle \frac{2375}{1000}$

Ab hier kannst du wie im Beispiel zuvor weiterrechnen und erhältst: $\frac{19}{8}=2{,}375$

Umrechnen durch schriftliches Dividieren

Es gibt auch Brüche, die man nicht so erweitern oder kürzen kann, dass eine Zehnerpotenz im Nenner steht wie zum Beispiel $\frac{5}{3}$ .

In jedem Fall kann man die Dezimalzahl durch schriftliches Dividieren erhalten.

Division mit endlichem Ergebnis

Beachte

Wenn man vollständig gekürzte Brüche hat, mit einem Produkt aus $2$ und/oder $5$ bzw. Potenzen davon im Nenner, erhält man als Ergebnis der schriftlichen Division eine endliche Dezimalzahl.

Beispiel

$\frac{16}{5}=16:5$

Dividiere schriftlich:

$\def\arraystretch{1.25} \begin{array}{rl}&16 : 5 = 3 \\-&\underline{15}& \\& \hphantom{1}10& \end{array}$

Die $5$ passt dreimal in die $16$ , es bleibt Rest $1$ .

Berechne $3\cdot5$ und ziehe das Ergebnis von $16$ ab.

$16-15=1\mathrm{ }$

$\def\arraystretch{1.25} \begin{array}{rl}&16 : 5 = 3{,}2 \\-&\underline{15} \\& \hphantom{1}10 \\-& \hphantom{1}\underline{10} \\&\hphantom{11}0\end{array}$

Die $5$ passt zweimal in die $10$ , also notiere $2$ als erste Stelle hinter dem Komma. Es bleibt kein Rest.

Insgesamt erhält man:

\displaystyle \frac{16}{5}=3{,}2

Division mit periodischem Ergebnis

Wenn der Nenner des vollständig gekürzten Bruches noch andere Primteiler als $2$ oder $5$ enthält (z.B. den Faktor 3 oder 7), erhält man eine periodische Dezimalzahl als Ergebnis der Division.

Beispiel

$\frac{17}{6}=17:6$

Dividiere schriftlich

$\def\arraystretch{1.25} \begin{array}{rl}&17 : 6 = 2 , 8333... \\-&\underline{12} \\& \hphantom{1}50 \\-& \underline{\hphantom{1}{48}} \\&\hphantom{…}20\\&-\underline{\hphantom{1}18}\\&\hphantom{- 11}20\\&\hphantom{1}-\underline{\hphantom{1}18}\\&\hphantom{- 1111}20\\&\hphantom{11}-\underline{\hphantom{1}18}\\&\hphantom{- 11111}20\\&\hphantom{1111111}...\end{array}$

Man merkt, dass sich die schriftliche Division an einer Stelle nun nur noch wiederholt. Es entsteht nur noch der Rest 2 und durch Erweitern auf 20 ist diese Zahl durch 18 teilbar, was $\textcolor{orange}{3}\cdot6$ entspricht. Daher ist $3$ unsere Periode.

Man schreibt $17:6=2{,}8\overline{3}$ und sagt "zwei Komma acht Periode drei".

Übungsaufgaben: Umrechnen von Brüchen in Dezimalzahlen

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Umwandeln von Brüchen und Dezimalbrüchen

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?