Nachtermin Teil A
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Gegeben ist die Funktion mit der Gleichung mit .
Ergänzen Sie die Wertetabelle auf zwei Stellen nach dem Komma gerundet.
Zeichnen Sie sodann den Graphen zu in das Koordinatensystem.
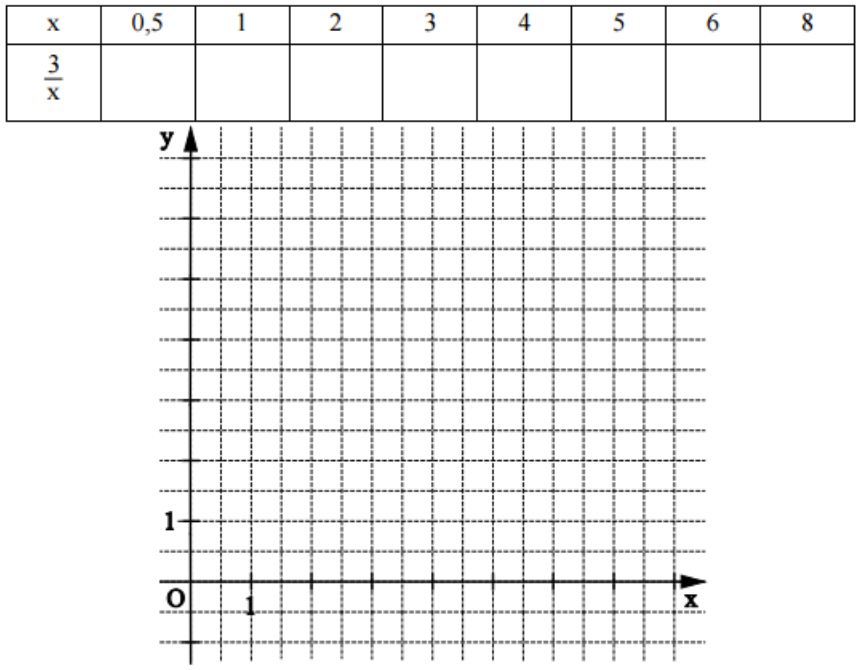
Punkte auf dem Graphen zu besitzen dieselbe Abszisse wie Punkte auf der Geraden mit der Gleichung mit .
Für sind die Punkte und Endpunkte von Strecken .
Zeichnen Sie die Gerade sowie die Strecke für in das Koordinatensystem zur Aufgabenstellung ein.
Unter den Strecken gibt es die Strecke mit .
Berechnen Sie den zugehörigen Wert für .
- 2
Die Skizze zeigt ein vereinfachtes Modell einer Windkraftanlage. Die drei Rotorblätter sind so angeordnet, dass sie eine drehsymmetrische Figur ergeben. Ein Mast dient zur Aufhängung der Rotorblätter.
Der Rotordurchmesser beträgt Meter (siehe Skizze).
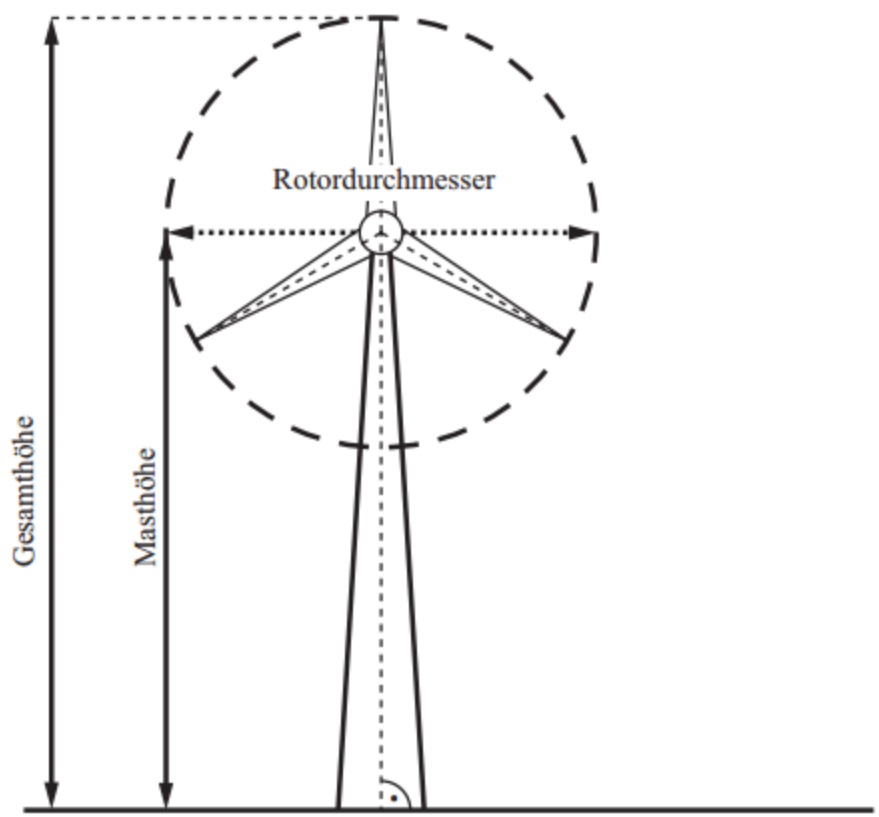
Für das Rotorblatt werden in Minuten Umdrehungen gezählt.
Berechnen Sie, welchen Weg die Spitze eines Rotorblattes nach einer Stunde unter denselben Bedingungen zurückgelegt hat.
Runden Sie das Ergebnis auf ganze Kilometer.
km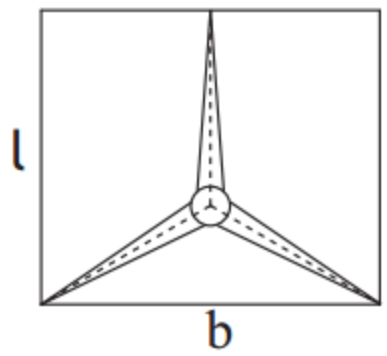
Die Skizze zeigt, wie die Rotorblätter in einem rechteckigen Feld in einer Montagehalle lagen, als man sie probeweise aneinander montierte.
Berechnen Sie die Seitenlängen und dieses rechteckigen Feldes.
Runden Sie auf ganze Meter.
m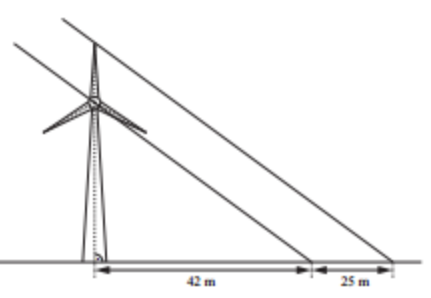
Die Sonne steht so, dass der Schatten des Rotorblattes, dessen Spitze senkrecht nach oben zeigt, lang ist. Der Schatten des Mastes endet in einer Entfernung von vom Mittelpunkt des Mastes (siehe Skizze).
Berechnen Sie die Gesamthöhe der Windkraftanlage. Runden Sie auf ganze Meter.
m
- 3
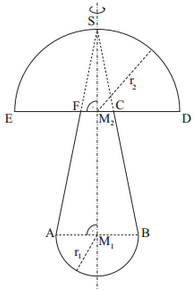
Die nebenstehende Skizze zeigt den Axialschnitt eines Rotationskörpers mit der Rotationsachse .
Es gilt:
Berechnen Sie die Länge der Strecken und .
Ergebnisse:
Berechnen Sie den Oberflächeninhalt des Körpers, der durch Rotation an der Achse entsteht. Runden Sie dabei auf eine Stelle nach dem Komma.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
