Aufgaben zu Daten und Zufallsexperimente
- 1
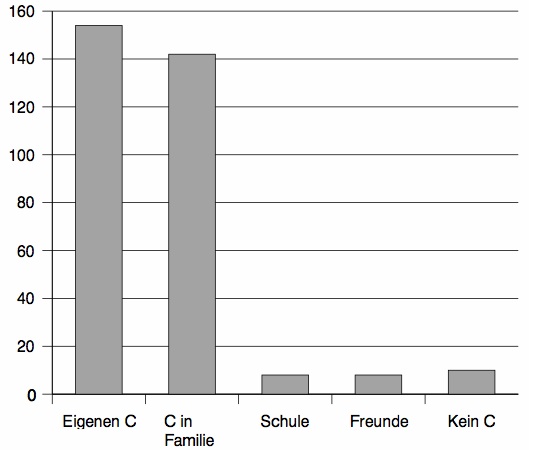
Von 322 Schülern haben 154 einen eigenen Computer, 142 einen Computerzugang in der Familie (aber keinen eigenen Computer), 8 haben einen Computerzugang in der Schule, 8 einen Computerzugang bei Freunden und 10 haben keinen Computerzugang.
Stelle die verschiedenen Arten des Computerzugangs in einem Diagramm dar.
- 2
Das Diagramm zeigt, wie viel Benzin sich zu jedem Zeitpunkt einer Reise im Tank eines Fahrzeugs befindet.
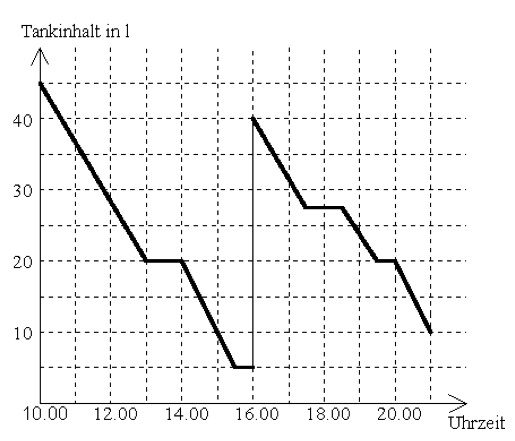
Beschreibe knapp, was um 16:00 Uhr geschieht.
EWie viele Liter Benzin hat das Auto auf der Reise von 10:00 Uhr bis 21:00 Uhr verbraucht?
l
- 3
In der Klasse 6e sind 28 Schüler.
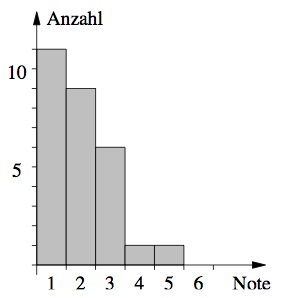
In der ersten Mathematikschulaufgabe, die sehr leicht war, ergab sich folgende Notenverteilung:
1
2
3
4
5
6
11
9
6
1
1
0
Stelle die Notenverteilung in einem Balkendiagramm dar und berechne die Durchschnittsnote.
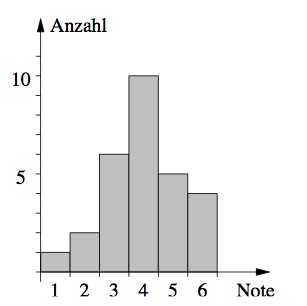
Nach dem Erfolg der ersten Schulaufgabe glaubten viele Schüler, dass man in Mathematik nicht viel lernen muss. Promt fiel die zweite Schulaufgabe sehr schlecht aus:
1
2
3
4
5
6
1
2
6
10
5
4
Stelle die Notenverteilung wieder in einem Balkendiagramm dar und berechne die Durchschnittsnote.
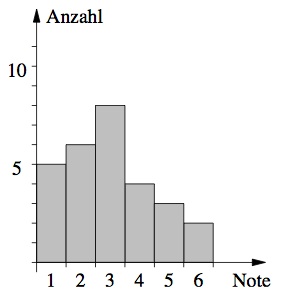
Die Durchschnittsnote der dritten Schulaufgabe war genau 3.
Finde eine mögliche Notenverteilung, in der jede Note von eins bis sechs mindestens einmal vorkommt und zeichne das Balkendiagramm der Verteilung.
- 4
Mit den Worten ”Im Jahr 2002 mussten wir zwar Verluste hinnehmen, aber wie Sie sehen, ging es 2003 wieder steil bergauf“ legt der Vorstand einer Firma dem Aufsichtsrat folgende Diagramme vor. Was würdest du als Aufsichtsrat dem Vorstand antworten?
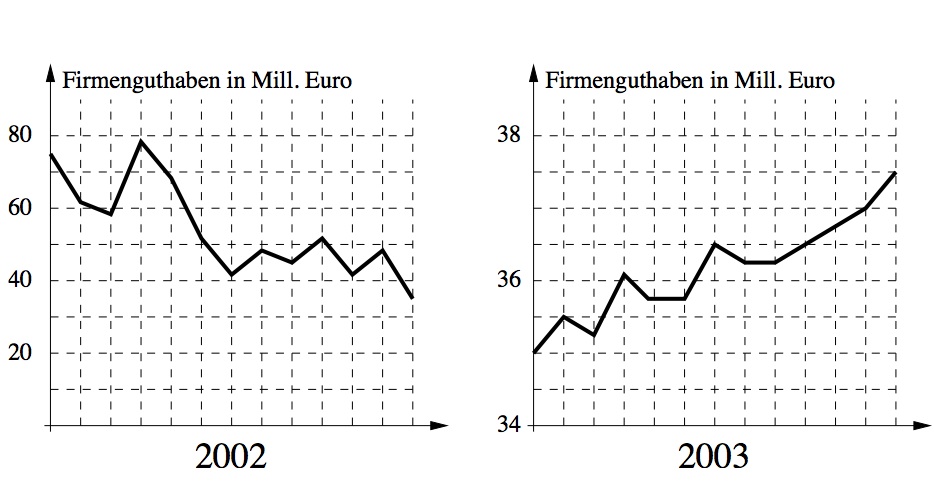
- 5
Drei L-Würfel werden gleichzeitig geworfen. Berechne die Wahrscheinlichkeiten folgender Ereignisse:
"Keine Sechs"
%"Genau eine Sechs"
%"Genau zweimal Sechs"
%"Alle drei Würfel zeigen Sechs"
%
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?