Aufgaben zu Funktionen als eindeutigen Zuordnungen
- 1
Anna und Basti sind zwei Sprinter des TSV Mathematika und wollen ein Sprintduell gegeneinander machen. Anna beschleunigt zwar langsamer als Basti, hat dafür aber eine höhere Endgeschwindigkeit. Nach ihrem Duell werden ihre Geschwindigkeiten als Graph in Abhängigkeit der Zeit in das folgende Diagramm gezeichnet.
Begründe, welcher der beiden Graphen zu welchem Läufer gehört.
- 2
Endlich Schulschluss! Miriam steht am Fahrradstellplatz, setzt ihre Schultasche in den Korb auf dem Gepäckträger ihres Fahrrads und packt, weil es ein warmer Sommertag ist, auch ihre Jacke dazu. Sie schließt das Schloss ihres Fahrrads auf und fährt los.
Nachdem sie ein Stück weit gekommen ist, muss sie an einer Ampel warten. Dort bemerkt sie, dass sie ihre Jacke verloren hat.
Sie kehrt um, findet die Jacke auf dem Boden liegend, hebt sie auf und verstaut sie sicher auf dem Gepäckträger. Dann setzt sie ihren Heimweg fort.
Das Zeit-Ort-Diagramm ihres Heimwegs sieht ungefähr so aus:
Beantworte die folgenden Fragen mit Hilfe des Diagramms:
Um wie viel Uhr ist Miriam von der Schule losgefahren?
Wie weit ist sie gefahren, bis sie zu der Ampel kam?
Wann ist sie an der Ampel angekommen, und wie lange hat sie dort gewartet, ehe sie umkehrte, um die Jacke zu suchen?
Wie weit von der Schule entfernt lag die Jacke auf dem Boden?
Wie viele Meter musste Miriam insgesamt zusätzlich fahren, weil sie die Jacke verloren hatte?
Musste Miriam auch beim zweiten Mal wieder an der Ampel warten, oder stand die Ampel diesmal auf Grün?
Wie weit ist Miriams Schulweg?
Wann kam Miriam vor ihrem Haus an?
Und überlege dir schließlich: Was könnte Miriam in der Zeit von 16:40 Uhr bis 16:45 Uhr getan haben?
- 3
Das Diagramm zeigt, wie viel Benzin sich zu jedem Zeitpunkt einer Reise im Tank eines Fahrzeugs befindet.
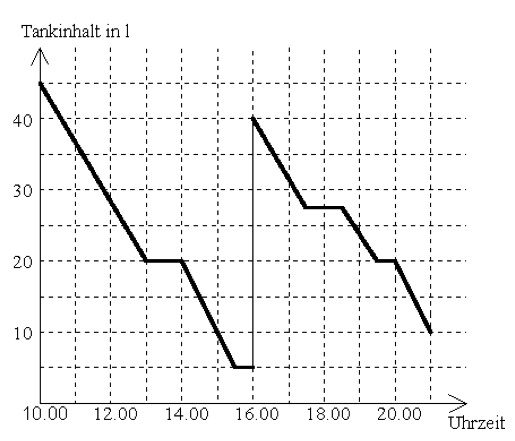
Beschreibe knapp, was um 16:00 Uhr geschieht.
EWie viele Liter Benzin hat das Auto auf der Reise von 10:00 Uhr bis 21:00 Uhr verbraucht?
l
- 4
In den folgenden Bildern A, B und C siehst du drei Graphen, die den gleichen Sachverhalt zeigen.
Die Preise sind in € angegeben.
a) Erkläre, worin sich die drei Graphen unterscheiden.
b) Finde Gemeinsamkeiten der drei Graphen.
c) Begründe, welche Darstellung du am geeignetsten findest.
- 5
Der Graph zeigt, wie ein Gefäß innerhalb von 10 Minuten mit Wasser gefüllt wird.
Bestimme, wie viel Wasser in den ersten 3 Minuten eingefüllt wird.
lBeschreibe, was zwischen der 6. und der 9. Minute passiert.
Lies ab, wie viel Liter Wasser in 10 Minuten insgesamt eingefüllt wird.
l
- 6
Auf folgenden Rennstrecken wurde die Geschwindigkeit einer Fahrerin in der 2. Runde gemessen.
Ordne die folgenden Geschwindigkeitsgraphen, den entsprechenden Rennstrecken zu. Begründe deine Entscheidung.
- 7
Welche der folgenden fünf Graphen gehören sicher nicht zu einer Funktion?
- 8
Wähle alle richtigen Aussagen aus:
- 9
Handelt es sich um eine Funktion oder nur um eine Zuordnung?
Einer Sängerin hat besonders erfolgreiche Lieder, auch Nummer 1 Hits genannt. Jedem Jahr wird die Anzahl dieser Nummer 1 Hits zugeordnet.
Diesmal wird die umgedrehte Richtung angeschaut:
Anzahl der Nummer 1 Hits Jahr
Du kaufst Äpfel und zahlst jeden einzelnen davon. Die betrachete Zuordnung ist: Anzahl Äpfel Preis
Wieder kaufst du Äpfel. Diesmal interessiert dich aber der Zusammenhang Preis Anzahl Äpfel
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?






























