In dieser Aufgabe bestimmst du mit dem Newton-Verfahren Nullstellen des Polynoms . Starte das Newton-Verfahren zunächst in , dann noch in .
Was beobachtest du?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Newtonschen Näherungsverfahren
Du sollst das Newton-Verfahren verwenden, um Nullstellen für f zu finden. Dabei wirst du sehen, dass das Newton-Verfahren nicht immer zu einer korrekten Lösung konvergiert.
Stelle zunächst die Rekursionsformel
auf. Berechne dafür die Ableitung . Ingesamt lautet damit die Rekursionsformel für
Starte nun das Verfahren wie verlangt mit .
Es gilt und , jeweils die beiden konstanten Koeffizienten von und . Deshalb gilt
Setze in Zähler und Nenner der Rekursionsformel ein:
Daher erhältst du insgesamt
An dieser Stelle brauchst du nicht weiterrechnen, denn . Du bist wieder beim Startwert angekommen, die Rekursion wird unendlich lang zwischen 0 und 2 springen. Dies ist ein Beispiel, bei dem das Newton-Verfahren fehlschlägt, weil es nur garantiert konvergiert, wenn du ausreichend nahe bei der Nullstelle beginnst.
Probiere daher als Nächstes den zweiten Startwert x_0 = 1. Einsetzen in Rekursionsformel ergibt:
Wiederhole diesen Schritt, bis sich der Wert kaum noch verändert:
Das Ergebnis hat sich kaum noch geändert, du erhältst die ungefähre Nullstelle . Das Verfahren ist in sehr wenigen Schritten konvergiert, da du bereits nahe an der Nullstelle begonnen hattest.
Anmerkung und Erläuterung: Am Polynom kannst du auch noch weitere interessante Phänomen beobachten. Betrachte dazu den Graph der Funktion.
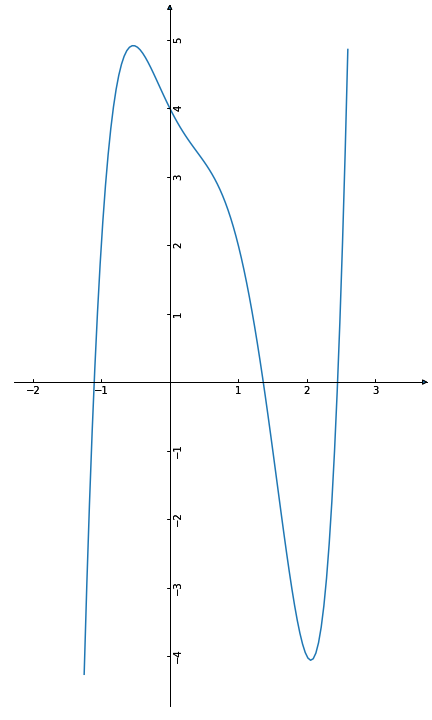
Erinnere dich, dass der Startwert 0 auf einen Wert in der Nähe der 2 abgebildet wird. In der Nähe von 2 liegt ein sehr spitzes lokales Minimum. Was bedeutet das für das Newtonverfahren? Nun, das Newton-Verfahren betrachtet immer die Tangente an den aktuellen Punkt. In der Nähe eines lokalen Minimums ändern sich die Tangenten sehr schnell.
Das bemerkst du, wenn du leicht von 0 abweichende Startwerte ausprobierst. Dabei musst du natürlich aufpassen, nicht zu stark zu runden, sonst landest du wieder bei dem Fall, den du oben berechnet hast.
Du kannst folgendes Konvergenzverhalten beobachten (die Werte sind mit dem Computer berechnet):
Startwert | Anzahl Schritte zur Konvergenz | Ungefähre Lösung |
|---|---|---|
| 15 | -1,103335 |
| 18 | 2,45032 |
| 8 | 1,365066 |
Bei sehr, sehr ähnlichen Startwerten ergeben sich drei vollkommen unterschiedliche Lösungen, die mit den drei Nullstellen im Graph übereinstimmen.
Bei sehr, sehr ähnlichen Startwerten ergeben also sich drei vollkommen unterschiedliche Lösungen, die mit den drei Nullstellen im Graph übereinstimmen. Im sehr kleinen Intervall von liegen also Startwerte, die gar nicht konvergieren oder zu völlig unterschiedlichen Lösungen führen.
Außerdem fällt dir in der Tabelle auf, dass die Anzahl der Schritte bis zur Konvergenz erheblich höher ist, als du vorher mit dem "braven" Startwert gesehen hattest.
Diese Beobachtungen unterstreichen erneut: Das Newton-Verfahren ist ein sehr effizientes lokales Verfahren. Ausreichend nahe an einer Nullstelle funktioniert es hervorragend. Ist man nicht nahe an einer Nullstelle, kann je nach Funktion und Startwert sehr unterschiedliches Verhalten auftreten.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
