Aufgaben zum Newtonschen Näherungsverfahren

Wie gut kannst du annähern? Mit diesen gemischten Übungsaufgaben lernst du, das Newton'sche Näherungsverfahren anzuwenden!

1
Berechne mit Hilfe des Newtonsches Näherungsverfahren die Nullstellen folgender Funktionen auf zwei Nachkommastellen genau.
1. $f(x)=x³-5x²-4x+2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Newton-Verfahren
  Wertetabelle
  $f(x)=x^3-5x^2-4x+2$
  Erstelle eine Wertetabelle um die Lage der Nullstellen einschränken zu können.
  x
  -3
  -2
  -1
  0
  1
  2
  3
  4
  5
  6
  f(x)
  -58
  -18
  0
  2
  -6
  -18
  -28
  -30
  -18
  14
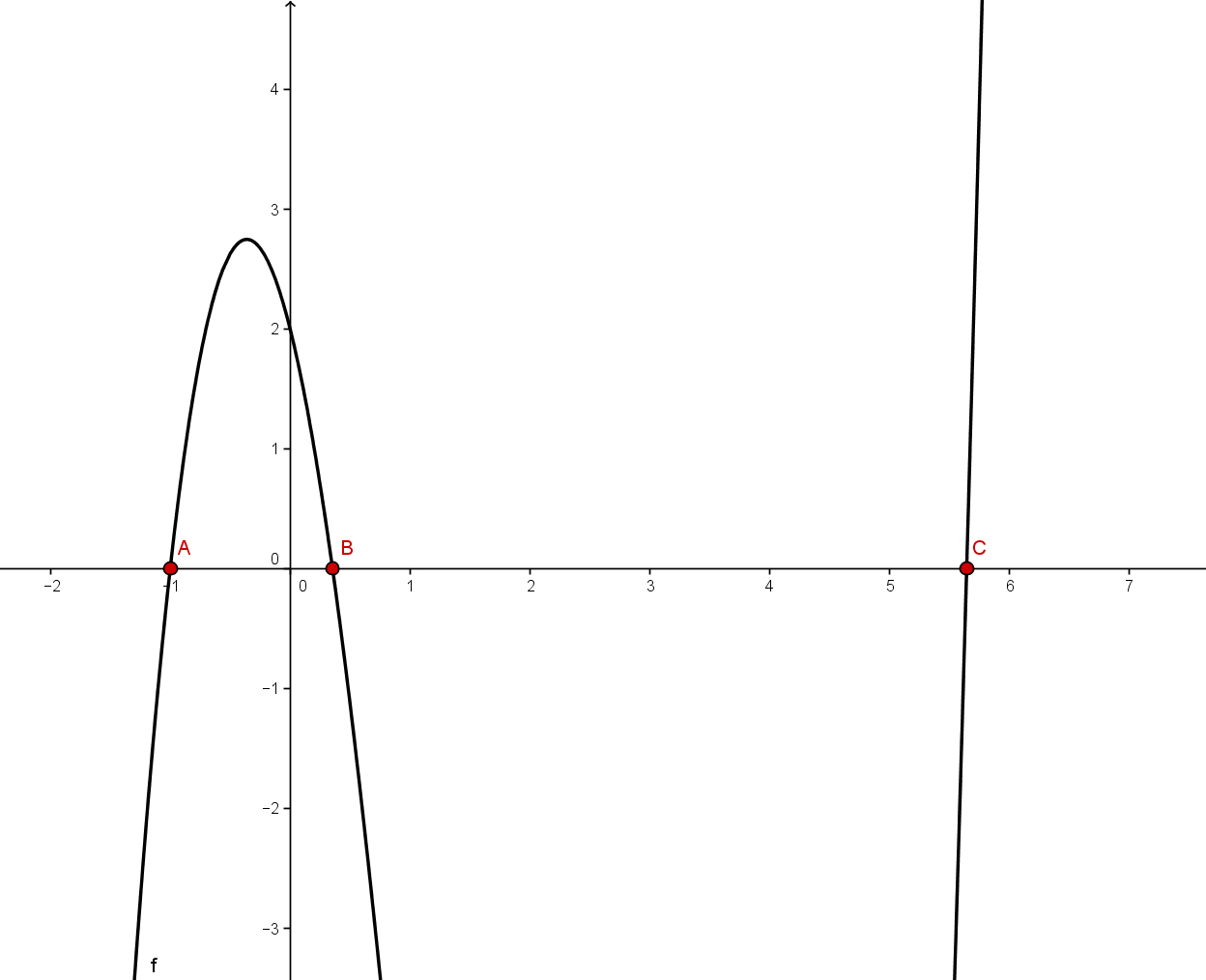
  Bestimmen der Intervalle
  Eine Nullstelle kann direkt aus der Tabelle abgelesen werden:
  $\tilde x_1=-1$
  Man sieht außerdem, dass die Funktion $f(x)$ in den Intervallen $]0;1[$ und $]5;6[$ ihr Vorzeichen ändert.
  Daraus folgt für die Nullstellen $\tilde x_{2{,}3}:$
  $\Rightarrow \tilde x_2\in \;]0;1[$ und $\tilde x_3\in\;]5;6[$
  Um die Intervalle weiter zu verkleinern und so einen besseren Anfangswert für das Newton-Verfahren zu bekommen, berechnet man den Funktionswert der Mittelwerte der ausgewählten Intervalle:
  x
  0
  0,5
  1
  5
  5,5
  6
  f(x)
  2
  -1,125
  -6
  -18
  -4,875
  14
  Man sieht nun, dass die Funktion $f(x)$ in den Intervallen $]0;0{,}5[$ und $]5{,}5;6[$ ihr Vorzeichen ändert.
  Daraus folgt für die Nullstellen $\tilde x_{2{,}3}:$
  $\Rightarrow \tilde x_2\in \;]0;0{,}5[$ und $\tilde x_3\in\;]5{,}5;6[$
  Anwenden des Newton-Verfahrens
  $f(x)=x^3-5x^2-4x+2$
  $f^\prime(x)=3x^2-10x-4$
  Bestimmen der Nullstellen
  Man wählt einen beliebigen Wert $x_0$ aus dem Intervall $]0;0{,}5[$ , z.B. $x_0=0{,}25$ .
  Man berechnet jetzt $x_1$ mit der oben angegebenen Rekursionsformel.
  Dann berechnet man $x_2$ mit dem gerade berechneten $x_1$ und der oben angegebenen Rekursionsformel.
  Dann berechnet man $x_3$ mit dem gerade berechneten $x_2$ und der oben angegebenen Rekursionsformel.
  Man erkennt jetzt, dass sich die Genauigkeit der Lösung im letzten Schritt nurnoch in der fünften Nachkommastelle verbessert.
  Da nur eine Angabe bis auf zwei Nachkommastellen gefordert war, ist man in diesem Schritt fertig und das Ergebnis lautet:
  Um $\tilde x_3$ zu bestimmen verfährt man analog und erhält für den Startwert $x_0=5{,}75$ folgende Werte:
  $i$
  0
  1
  2
  3
  $x_i$
  $5{,}75$
  $5{,}649253731$
  $5{,}645755468$
  $5{,}645751311$
  Und somit erhält man:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $f(x)=\ln(x^4+5x³-5)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Newton-Verfahren
  $f(x)=\ln(x^4+5x^3-5)$
  Der natürliche Logarithmus $\ln(x)$ ist nur auf den positiven, reellen Zahlen definiert.
  Um die Nullstellen der Funktion $f(x)$ zu bestimmen macht man zuvor eine kurze Vorüberlegung.
  Man betrachtet die Nullstellen des natürlichen Logarithmus und stellt folgendes fest:
  Sei $g(x)=\ln(x)$ :
  $g(x)=0 \Leftrightarrow \ln(x)=0 \qquad \qquad \qquad\vert\ e$
  $e^{\ln(x)}=e^0 \qquad \qquad \qquad \qquad \qquad \quad$ Umformen.
  $\Rightarrow x=1$
  Man sieht, dass $x=1$ die einzige Nullstelle von $\ln(x)$ ist.
  Um die Nullstellen von $f(x)$ zu approximieren, kann man also die "Einsstellen" der Funktion $h(x)=x^4+5x^3-5$ approximieren, d.h. man sucht die Lösung für die Gleichung $h(x)=x^4+5x^3-5=1$ .
  Da das Newtonverfahren Nullstellen approximiert macht man eine kleine Umformung und erhält:
  $h(x)=x^4+5x^3-5=1 \qquad \qquad \vert -1$
  $x^4+5x^3-6=0$
  Wir approximieren also die Nullstellen der Funktion $\tilde h(x)=x^4+5x^3-6$ um die Nullstellen von $f(x)$ zu finden.
  Wertetabelle
  $x$
  -6
  -5
  -4
  -3
  -2
  -1
  0
  1
  2
  $\tilde h(x)$
  210
  -6
  -70
  -60
  -30
  -10
  -6
  0
  50
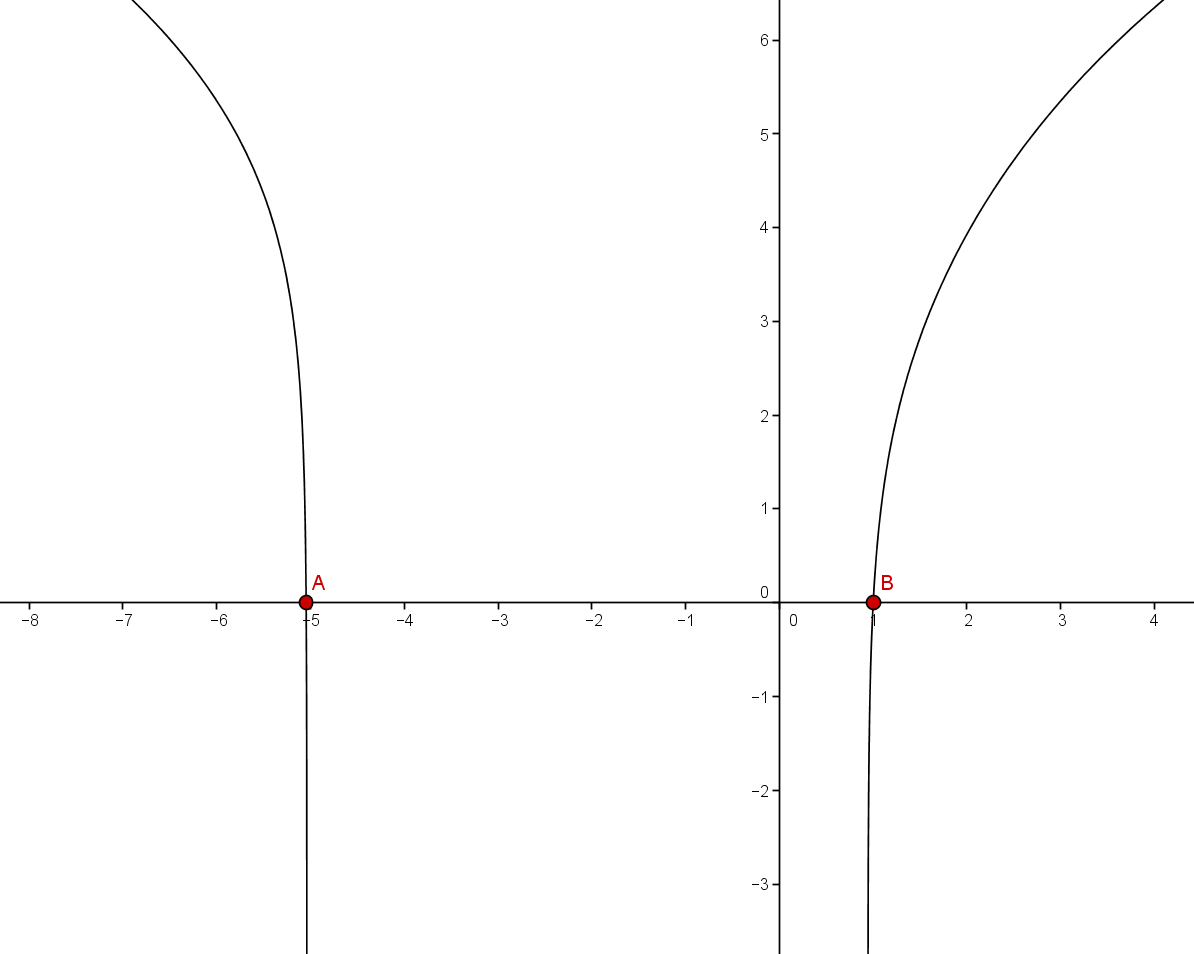
  Bestimmen der Intervalle
  Eine Nullstelle kann direkt aus der Tabelle abgelesen werden:
  $\tilde x_1=1$
  Man sieht außerdem, dass die Funktion $\tilde h(x)$ im Intervallen $]-6;-5[$ ihr Vorzeichen ändert.
  Daraus folgt für die Nullstellen $\tilde x_{2}:$
  $\Rightarrow \tilde x_2\in \;]-6;-5[$
  Um das Intervall weiter zu verkleinern und so einen besseren Anfangswert für das Newton-Verfahren zu bekommen, berechnet man den Funktionswert der Mittelwerte der ausgewählten Intervalle:
  x
  -6
  -5,5
  -5
  f(x)
  210
  77,1875
  -6
  Man sieht nun, dass die Funktion $\tilde h(x)$ in den Intervallen $]-5{,}5;-5[$ ihr Vorzeichen ändert.
  Daraus folgt für die Nullstellen $\tilde x_{2}:$
  $\Rightarrow \tilde x_2\in \;]-5{,}5;-5[$
  Anwenden des Newton-Verfahrens
  $\tilde h(x)=x^4+5x^3-6$
  $\tilde{h}^\prime(x)=4x^3+15x^2$
  Bestimmen der Nullstellen
  Man wählt einen beliebigen Wert $x_0$ aus dem Intervall $]-5{,}5;-5[$ , z.B. $x_0=-5{,}25$ .
  Man berechnet jetzt $x_1$ mit der oben angegebenen Rekursionsformel.
  $=-5{,}067531179\approx-5{,}06753$
  Dann berechnet man $x_2$ mit dem gerade berechneten $x_1$ und der oben angegebenen Rekursionsformel.
  $=-5{,}046930085\approx-5{,}04693$
  Dann berechnet man $x_3$ mit dem gerade berechneten $x_2$ und der oben angegebenen Rekursionsformel.
  $=-5{,}046680361\approx-5{,}04668$
  Man erkennt jetzt, dass sich die Genauigkeit der Lösung im letzten Schritt nur noch in der vierten Nachkommastelle verbessert.
  Da nur eine Angabe bis auf zwei Nachkommastellen gefordert war, ist man in diesem Schritt fertig und das Ergebnis lautet:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Bestimme $\pi$ mit Hilfe des Newton-Verfahrens auf vier Dezimalstellen genau.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Das Newton-Verfahren
Du sollst das Newton-Verfahren verwenden, um $\pi$ zu bestimmen. Das Newton-Verfahren dient dazu, Nullstellen von Funktionen zu bestimmen. Zunächst benötigst du also eine Funktion $f(x)$ , die $\pi$ als Nullstelle hat, also $f(\pi) = 0$ erfüllt.
Erinnere dich, dass $\sin(\pi) = 0$ . Ein guter Kandidat ist also $f(x) = \sin(x)$ . (Es gibt unendlich viele weitere Mögllichkeiten, dies ist nur die einfachste.)
Im Newton-Verfahren wendest du Iterationen der Rekursionsformel
an. Berechne dafür die Ableitung von $f$ , sie lautet $f'(x) = \cos(x)$ . Die Rekursionsformel des Newton-Verfahren für diese Aufgabe lautet also
Alternative: Du kannst dir die folgenden Rechnungen einfacher machen, wenn du dich an folgenden Zusammenhang aus der Trigonometrie erinnerst:
Die Lösung wird allerdings den ausführlichen Weg präsentieren.
Erstelle nun eine Wertetabelle, um den Startwert für das Verfahren in die Nähe der Nullstelle zu bringen. Erinnere dich, dass $\pi \approx 3$ .
$x$
2
3
4
$\sin(x)$
0,909
0,141
-0.757
In der Tat liegt die Nullstelle $\pi$ zwischen 3 und 4, denn dort wechselt der Sinus sein Vorzeichen.
Wähle einen Startwert. Jeder Startwert im Intervall $[3; 4[$ ist sinnvoll, z.B. $x_0 = 3%$ . Setze diesen in die Rekursionsformel ein:
Setze den Wert wiederholt in die Rekursionsformel ein, bis du die gewünschte Genauigkeit erhältst:
Du siehst, dass sich in den letzten beiden Iterationen die ersten sieben Nachkommastellen nicht geändert haben. Du hast daher sogar eine (mindestens) sechs Nachkommastellen genaue Lösung gefunden, genauer als verlangt.
Somit erhältst du, dass $\sin(3{,}141593) \approx 0$ , und damit auch $\pi \approx 3{,}141593$ .
Tipp: Finde eine Funktion, für die $\pi$ eine Nullstelle ist. Denke zurück an trigonometrische Funktionen.
3
Bestimme $\sqrt 5$ mit Hilfe des Newton-Verfahrens auf drei Dezimalstellen genau.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Newtonschen Näherungsverfahren
Tipp: Finde eine Funktion, für die $\sqrt{5}$ eine Nullstelle ist.
Du sollst das Newton-Verfahren verwenden, um $\sqrt 5$ zu bestimmen. Das Newton-Verfahren dient dazu, Nullstellen von Funktionen zu bestimmen. Zunächst benötigst du also eine Funktion $f(x)$ , die $\sqrt 5$ als Nullstelle hat, also $f(\sqrt 5) = 0$ erfüllt.
$\sqrt 5$ ist die Zahl, für die $\sqrt{5}^2 = 5$ gilt, also auch $\sqrt{5}^2 - 5 = 0$ . Ein guter Kandidat für die gesuchte Funktion ist daher $f(x) = x^2 - 5$ . (Es gibt unendlich viele weitere Möglichkeiten, dies ist nur die einfachste.)
Im Newton-Verfahren wendest du Iterationen der Rekursionsformel
an. Berechne dafür die Ableitung von $f$ , sie lautet $f'(x) = 2x$ . Die Rekursionsformel des Newton-Verfahren für diese Aufgabe lautet also
Erstelle nun eine Wertetabelle, um den Startwert für das Verfahren in die Nähe der Nullstelle zu bringen. Bedenke, dass du nur positive Werte betrachten musst, da die Wurzel immer positiv ist.
$x$
1
2
3
$f(x)$
-4
-1
4
Du siehst, dass die Nullstelle zwischen 2 und 3 liegt. Dort wechselt $f$ sein Vorzeichen. Teste nun noch den Mittelwert 2,5: $f(2{,}5) = 1{,}25$ .
Das bedeutet, dass die Nullstelle $\sqrt 5$ im Intervall $]2; 2{,}5[$ liegt.
Jeder Startwert im Intervall $]2; 2{,}5[$ ist sinnvoll, z.B. $x_0 = 2$ . Setze diesen in die Rekursionsformel ein:
Setze den neuen Wert nun so lang in die Rekursionsformel ein, bis du die gewünschte Genauigkeit erhältst:
Du siehst, dass sich in den letzten beiden Iterationen nur noch die vierte Nachkkommastelle geändert hat.
Somit erhältst du, dass $f(2{,}236) \approx 0$ , und damit auch $\sqrt 5 \approx 2{,}236$ .

x	-3	-2	-1	0	1	2	3	4	5	6
f(x)	-58	-18	0	2	-6	-18	-28	-30	-18	14

x	0	0,5	1	5	5,5	6
f(x)	2	-1,125	-6	-18	-4,875	14

$i$	0	1	2	3
$x_i$	$5{,}75$	$5{,}649253731$	$5{,}645755468$	$5{,}645751311$

$x$	-6	-5	-4	-3	-2	-1	0	1	2
$\tilde h(x)$	210	-6	-70	-60	-30	-10	-6	0	50

x	-6	-5,5	-5
f(x)	210	77,1875	-6

$x$	2	3	4
$\sin(x)$	0,909	0,141	-0.757

$x$	1	2	3
$f(x)$	-4	-1	4

In dieser Aufgabe bestimmst du mit dem Newton-Verfahren Nullstellen des Polynoms $f(x) =x^5-3x^4+x^3+x^2-2x+4$ . Starte das Newton-Verfahren zunächst in $x_0 = 0$ , dann noch in $x_0 = 1$ .

Was beobachtest du?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Newtonschen Näherungsverfahren

Du sollst das Newton-Verfahren verwenden, um Nullstellen für f zu finden. Dabei wirst du sehen, dass das Newton-Verfahren nicht immer zu einer korrekten Lösung konvergiert.

Stelle zunächst die Rekursionsformel

\displaystyle x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}

auf. Berechne dafür die Ableitung $f'(x) =5x^4-12x^3+3x^2+2x-2$ . Ingesamt lautet damit die Rekursionsformel für $f$

\displaystyle x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}

Starte nun das Verfahren wie verlangt mit $x_0 = 0$ .

Es gilt $f(x_0) = 4$ und $f'(x_0) = -2$ , jeweils die beiden konstanten Koeffizienten von $f$ und $f'$ . Deshalb gilt

\displaystyle x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}

Setze $x_1$ in Zähler und Nenner der Rekursionsformel ein:

\displaystyle x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}

\displaystyle x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}

Daher erhältst du insgesamt

\displaystyle x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}

An dieser Stelle brauchst du nicht weiterrechnen, denn $x_0 = x_2$ . Du bist wieder beim Startwert angekommen, die Rekursion wird unendlich lang zwischen 0 und 2 springen. Dies ist ein Beispiel, bei dem das Newton-Verfahren fehlschlägt, weil es nur garantiert konvergiert, wenn du ausreichend nahe bei der Nullstelle beginnst.

Probiere daher als Nächstes den zweiten Startwert x_0 = 1. Einsetzen in Rekursionsformel ergibt:

\displaystyle x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}

Wiederhole diesen Schritt, bis sich der Wert kaum noch verändert:

\displaystyle x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}

\displaystyle x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}

Das Ergebnis hat sich kaum noch geändert, du erhältst die ungefähre Nullstelle $x=1{,}3651$ . Das Verfahren ist in sehr wenigen Schritten konvergiert, da du bereits nahe an der Nullstelle begonnen hattest.

Anmerkung und Erläuterung: Am Polynom $f$ kannst du auch noch weitere interessante Phänomen beobachten. Betrachte dazu den Graph der Funktion.

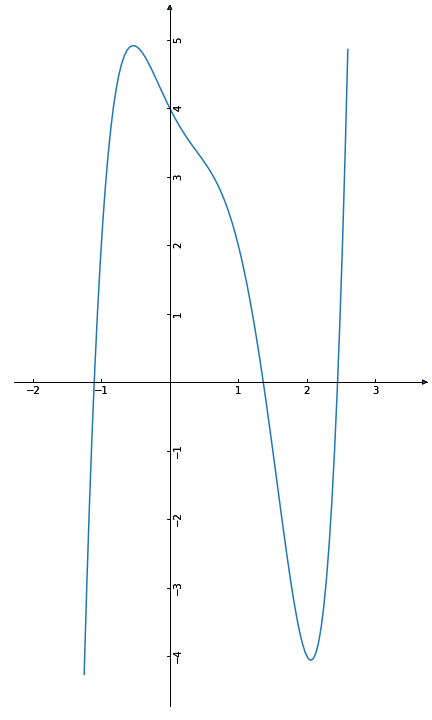
Erinnere dich, dass der Startwert 0 auf einen Wert in der Nähe der 2 abgebildet wird. In der Nähe von 2 liegt ein sehr spitzes lokales Minimum. Was bedeutet das für das Newtonverfahren? Nun, das Newton-Verfahren betrachtet immer die Tangente an den aktuellen Punkt. In der Nähe eines lokalen Minimums ändern sich die Tangenten sehr schnell.

Das bemerkst du, wenn du leicht von 0 abweichende Startwerte ausprobierst. Dabei musst du natürlich aufpassen, nicht zu stark zu runden, sonst landest du wieder bei dem Fall, den du oben berechnet hast.

Du kannst folgendes Konvergenzverhalten beobachten (die Werte sind mit dem Computer berechnet):

Startwert $x_0$	Anzahl Schritte $n$ zur Konvergenz	Ungefähre Lösung $x_n$
$10^{-7}$	15	-1,103335
$10^{-5}$	18	2,45032
$10^{-3}$	8	1,365066

Bei sehr, sehr ähnlichen Startwerten ergeben sich drei vollkommen unterschiedliche Lösungen, die mit den drei Nullstellen im Graph übereinstimmen.

Bei sehr, sehr ähnlichen Startwerten ergeben also sich drei vollkommen unterschiedliche Lösungen, die mit den drei Nullstellen im Graph übereinstimmen. Im sehr kleinen Intervall von $[0;0{,}0001]$ liegen also Startwerte, die gar nicht konvergieren oder zu völlig unterschiedlichen Lösungen führen.

Außerdem fällt dir in der Tabelle auf, dass die Anzahl der Schritte bis zur Konvergenz erheblich höher ist, als du vorher mit dem "braven" Startwert $x_0 = 1$ gesehen hattest.

Diese Beobachtungen unterstreichen erneut: Das Newton-Verfahren ist ein sehr effizientes lokales Verfahren. Ausreichend nahe an einer Nullstelle funktioniert es hervorragend. Ist man nicht nahe an einer Nullstelle, kann je nach Funktion und Startwert sehr unterschiedliches Verhalten auftreten.

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

5
Berechne $\sqrt[3]{12}$ mit 4 Iterationen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Newtonsches Näherungsverfahren
$n$
$x_n$
0
2
1
2,33333
2
2,29024931
3
2,289428779
4
2,289428485
Die ersten 6 Nachkommastellen sind richtig.
$\left(x^n\right)'=nx^{n-1}$

$n$	$x_n$
0	2
1	2,33333
2	2,29024931
3	2,289428779
4	2,289428485

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Aufgaben zum Newtonschen Näherungsverfahren

Wertetabelle

Bestimmen der Intervalle

Anwenden des Newton-Verfahrens

Bestimmen der Nullstellen

Hast du eine Frage oder Feedback?

Wertetabelle

Bestimmen der Intervalle

Anwenden des Newton-Verfahrens

Bestimmen der Nullstellen

Hast du eine Frage oder Feedback?