Aufgaben zur Umkehrfunktion
Wie gut kennst du dich aus? Vertiefe dein Wissen mit diesen gemischten Übungsaufgaben zur Umkehrfunktion.
- 1
Bilde die Umkehrfunktion und gib falls nötig einen neuen Definitionsbereich an.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umkehrfunktion
Definitionsmenge und Wertebereich
Die Definitionsmenge der Funktion wird zum Wertebereich der Umkehrfunktion .
Der Wertebereich der Funktion wird zur Defininitionsmenge der Umkehrfunktion .
Umkehrfunktion
Vertausche die Variablen und .
Löse nach auf.
Man kann jetzt die Definitionsmenge und den Wertebereich angeben und sieht die Übereinstimmung mit der obigen Überlegung.
und
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umkehrfunktion
Definitionsmenge und Wertebereich
Die Definitionsmenge der Funktion wird zum Wertebereich der Umkehrfunktion .
Der Wertebereich der Funktion wird zur Defininitionsmenge der Umkehrfunktion .
Umkehrfunktion
Vertausche die Variablen und .
Löse nach auf.
Man kann jetzt die Definitionsmenge und den Wertebereich angeben und sieht die Übereinstimmung mit der obigen Überlegung.
und
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umkehrfunktion
Definitionsmenge und Wertebereich
Da die Funktion eine um 1 nach unten geschobene Parabel ist und somit Werte aus ihrem Wertebereich mehrmals "trifft" muss ihr Definitionsbereich eingeschränkt werden, um eine Umkehrfunktion zu finden.
Durch Überlegung
Da symmetrisch zu ist sieht man, dass man wählen muss.
Durch Rechnung
Man errechnet, wie unten gezeigt, die Umkehrfunktion und betrachtet die Wertemenge der Umkehrfunktion um die Einschränkung des Definitionsbereichs von anzugeben.
Die Definitionsmenge der Funktion wird zum Wertebereich der Umkehrfunktion .
Der Wertebereich der Funktion wird zur Defininitionsmenge der Umkehrfunktion .
Umkehrfunktion
Vertausche die Variablen und .
Löse nach auf.
Da die Umkehrfunktion im Wertebereich liegen soll, wähle die positive Lösung der Gleichung.
Man kann jetzt die Definitionsmenge und den Wertebereich angeben und sieht die Übereinstimmung mit der obigen Überlegung.
und
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umkehrfunktion
Definitionsmenge und Wertebereich
Die Definitionsmenge der Funktion wird zum Wertebereich der Umkehrfunktion .
Der Wertebereich der Funktion wird zur Defininitionsmenge der Umkehrfunktion .
Umkehrfunktion
Vertausche die Variablen und .
Löse nach auf.
und
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umkehrfunktion
Definitionsmenge und Wertebereich
Da die Funktion eine Parabel ist und somit Werte aus ihrem Wertebereich mehrmals "trifft" muss ihr Definitionsbereich eingeschränkt werden, um eine Umkehrfunktion zu finden.
Durch Überlegung
Man muss die Symmetrieachse der Parabel bestimmen. Da der Scheitelpunkt auf der Symmetrieachse liegt bestimmt man diesen.
Der Scheitelpunkt ist .
Also ist symmetrisch zu und man muss wählen.
Durch Rechnung
Man errechnet, wie unten gezeigt, die Umkehrfunktion und betrachtet die Wertemenge der Umkehrfunktion um die Einschränkung des Definitionsbereichs von anzugeben.
Die Definitionsmenge der Funktion wird zum Wertebereich der Umkehrfunktion .
Der Wertebereich der Funktion wird zur Defininitionsmenge der Umkehrfunktion .
Umkehrfunktion
Da die Umkehrfunktion im Wertebereich liegen soll, wähle die positive Lösung der Wurzel.
Man kann jetzt die Definitionsmenge und den Wertebereich angeben und sieht die Übereinstimmung mit der obigen Überlegung.
und
Hast du eine Frage oder Feedback?
- 2
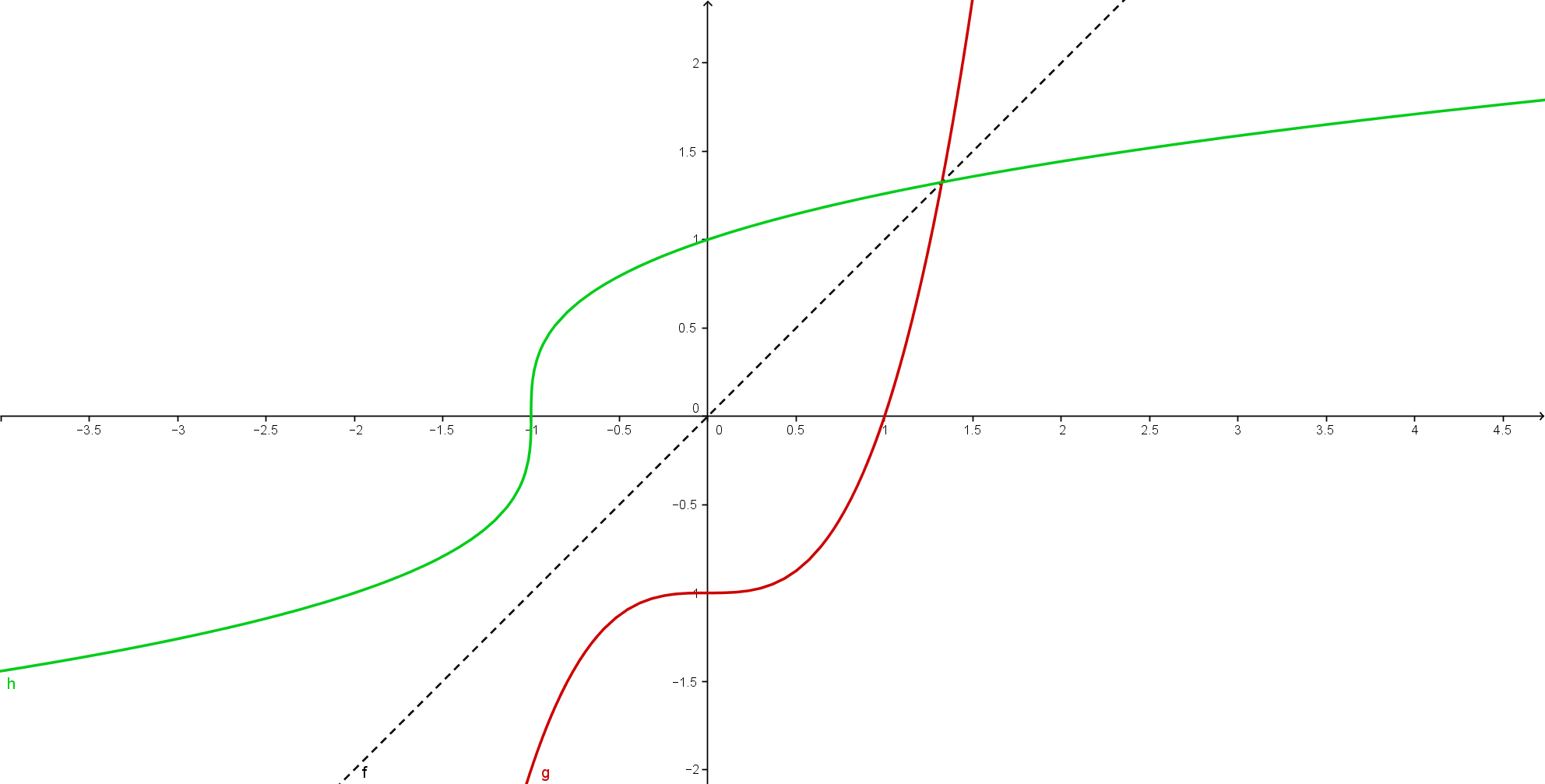
Bilde die Umkehrfunktion zu graphisch.
Zeichne die Funktion in ein Koordinatensystem: Verschiebung von um -1 in y-Richtung
Zeichne die Winkehalbierende des ersten und dritten Quadranten.
Spiegele die Funktion an der Winkelhalbierenden.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?