Die Wertemenge (oder Bildmenge) einer Funktion ist die Menge aller möglichen Funktionswerte, die herauskommen können, wenn man alle Zahlen aus der Definitionsmenge in die Funktion einsetzt.
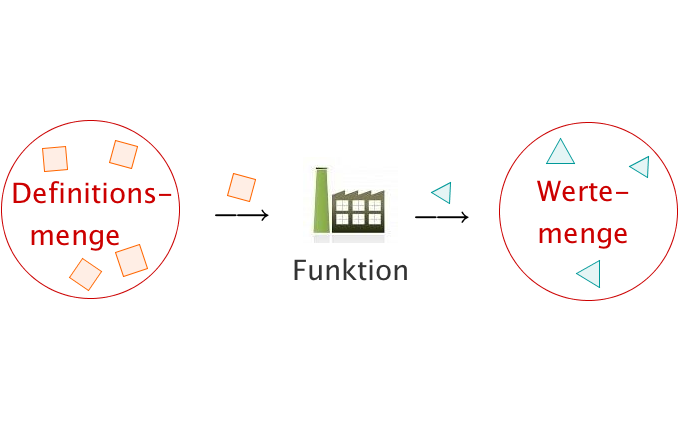
Unterschied zwischen Wertemenge und Zielmenge
In der Wertemenge befinden sich nur die Werte, die wirklich von der Funktion angenommen werden.
Die Zielmenge ist eine Menge, in der die Wertemenge enthalten ist, in der es aber auch noch weitere Elemente gibt. So ist z. B. eine Zielmenge der Funktion die Menge der reellen Zahlen . Die eigentliche Wertemenge ist aber (alle positiven reellen Zahlen und die Null), da keine negativen Zahlen von der Funktion angenommen werden.
Ein anderes Wort für Zielmenge ist Wertevorrat.
Weitere Beispiele
Funktion | (eine) Zielmenge | (die) Wertemenge |
|---|---|---|
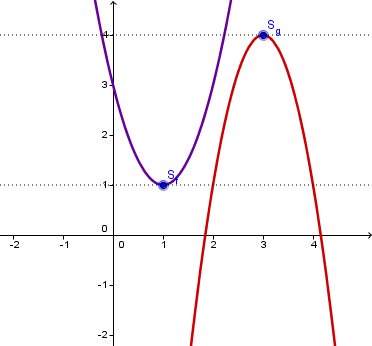
Die Wertemenge einer quadratischen Funktion lässt sich leicht bestimmen, wenn die Funktion in der Scheitelform gegeben ist. Ist die Parabel nach oben geöffnet, so ist die Wertemenge durch gegeben, ist sie nach unten geöffnet, so lautet die Wertemenge .
So ist z. B. die Wertemenge der Funktion gegeben durch und die der Funktion durch .
Video zur Bestimmung des Definitions- u. Wertebereichs
Laden
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Bestimmung von Wertebereichen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
