Das "Felder-Abstreichen" ist eine Methode, die dazu dient, nur mithilfe der Nullstellen einen ungefähren Überblick über den Verlauf des Graphen zu erhalten.
Sie wird normalerweise auf Polynomfunktionen angewandt.
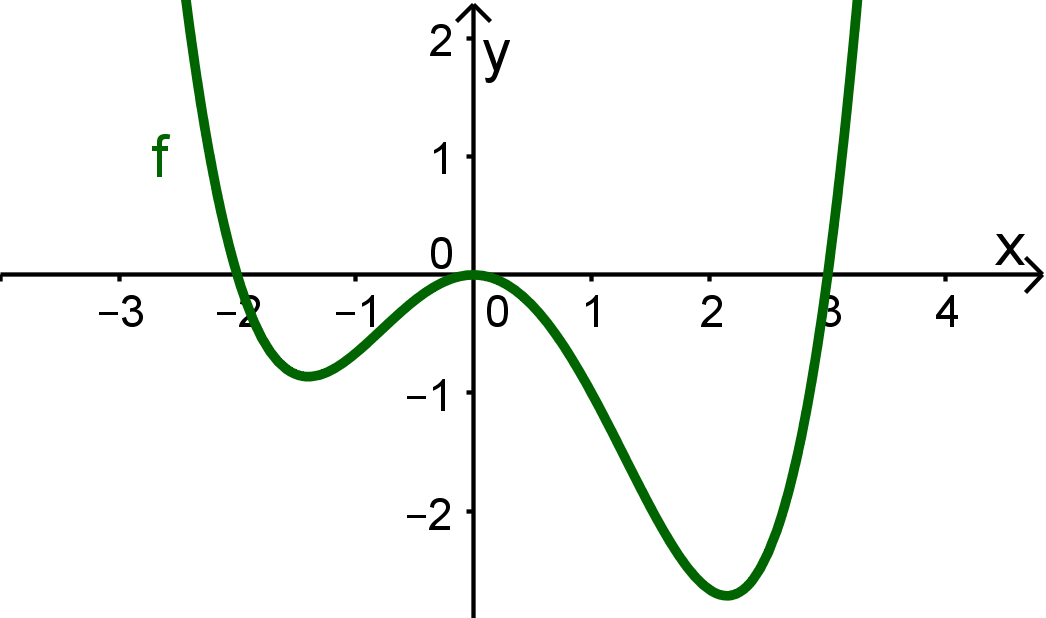
Funktion, gegeben durch Funktionsterm
Graph der Funktion
Vorgehensweise
Beim Felder-Abstreichens geht man in folgenden Schritten vor:
Nullstellen der Funktion bestimmen
Koordinatensystem anlegen und Bereiche abgrenzen
Vorzeichen der Funktion in den einzelnen Bereichen ermitteln und Felder kennzeichnen, durch die der Graph verläuft bzw. nicht verläuft ("Felder abstreichen")
Ungefähren Graphenverlauf einzeichnen
Tipps und Details, Vorgehensweise am Beispiel
Erster Schritt: Nullstellen bestimmen
Als Erstes muss man die Nullstellen der Funktion herausfinden. Wie das im Einzelnen geht, hängt natürlich von der Funktion ab.
Im Beispiel:
Die Funktion sei gegeben durch Funktionsterm
Wenn man die Nullstellen von dieser Funktion bestimmt, erhält man nach einiger Rechnung:
Zweiter Schritt: Graphik anlegen
Dann
legt man ein Koordinatensystem an,
trägt die Nullstellen ein,
und grenzt die Bereiche ab.
Dazu zieht man bei den Nullstellen jeweils eine dünne, zur x-Achse senkrechte Hilfslinie als "Grenzlinie" zwischen den Bereichen.
(Außerdem muss man solche Grenzlinien ziehen bei Definitionslücken und bei Sprungstellen der Funktion; bei Polynomfunktionen gibt es aber weder Definitionslücken noch Sprungstellen.)
Im Beispiel:
Skizziertes Koordinatensystem mit den abgegrenzten Bereichen:
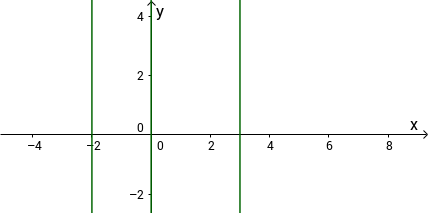
Hier sind bei den Nullstellen -2, 0 und 3 jeweils Linien eingezeichnet, um die Bereiche abzugrenzen.
Dritter Schritt: Vorzeichen der einzelnen Bereiche ermitteln, Felder kennzeichnen
Vorzeichen ermitteln
Als nächstes bestimmt man das Vorzeichen der Funktionswerte in jedem der Bereiche.
Dazu braucht man einfach nur für jeden Bereich einen x-Wert in die Funktion einzusetzen.
Im Beispiel:
für
für
für
für
Bei Polynomfunktionen kann man das Vorzeichen für die späteren Bereiche auch mit der Vielfachheit der Nullstellen erschließen.
Felder kennzeichnen
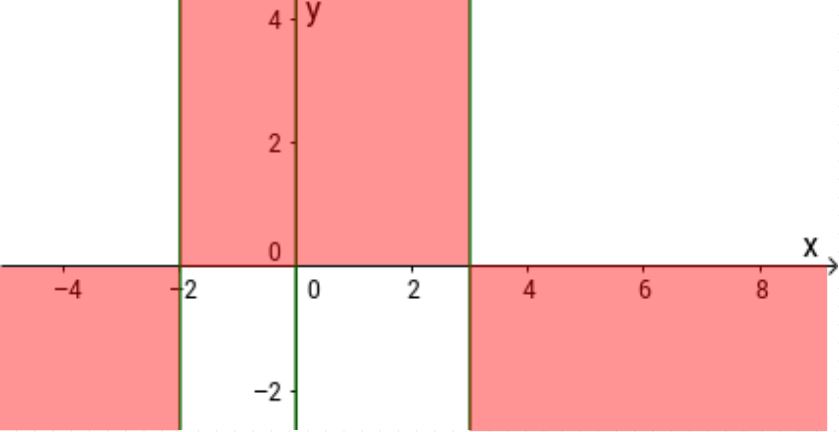
Wenn man die Vorzeichen kennt, streicht man üblicherweise für jeden Bereich dasjenige Feld weg, durch das der Graph sicher nicht verläuft, also
das Feld unterhalb der x-Achse, falls die Funktionswerte positiv sind,
bzw. das Feld oberhalb der x-Achse, falls die Funktionswerte negativ sind.
Vierter Schritt: Groben Graphenverlauf einzeichnen
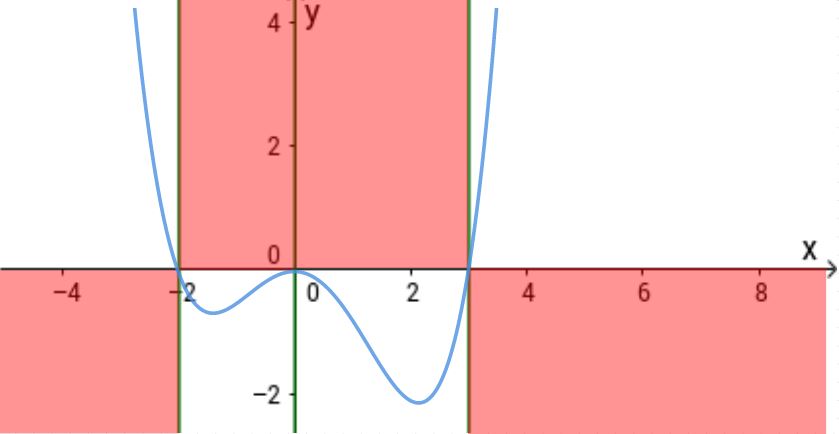
Nachdem man alle "verbotenen" Bereiche weggestrichen hat, zeichnet man aus der freien Hand den ungefähren Verlauf des Graphen durch die "erlaubten" Felder ein.
Der Graph muss auf jeden Fall alle Nullstellen passieren und darf nicht durch den roten Bereich verlaufen.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
