Eine Linearkombination von Vektoren ist eine Summe von Vektoren (Vektoraddition), wobei jeder Vektor noch mit einer reellen Zahl (dem sogenannten Linearfaktor) multipliziert werden kann. Das Ergebnis davon ist wieder ein Vektor.
Hierbei sind , und
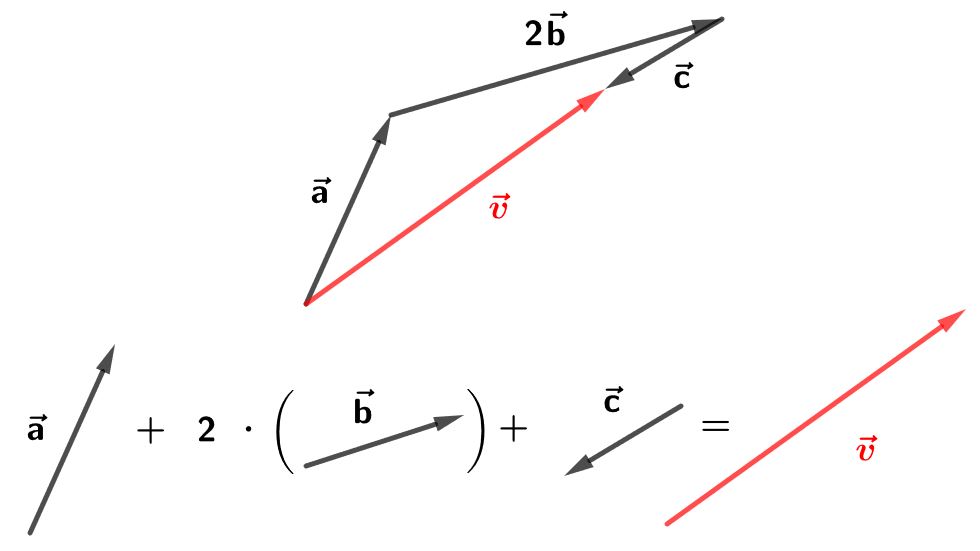
Darstellung eines Vektors als Linearkombination von anderen Vektoren
Im obigen Beispiel ist der Vektor eine Linearkombination aus den Vektoren , und .
Beispiel
Der Vektor soll als Linearkombination der Vektoren , und geschrieben werden. Eine Möglichkeit dafür ist:
.
Beispiele für Linearkombinationen
Der Vektor soll als Linearkombination der Vektoren , und dargestellt werden. Dazu muss folgendes lineares Gleichungssystem gelöst werden:
In diesem Fall ist und , also:
Der Vektor soll als Linearkombination der Vektoren und dargestellt werden. Dazu muss folgendes lineares Gleichungssystem gelöst werden:
Man wird feststellen, dass dies nicht möglich ist. Der Vektor ist also keine Linearkombination der Vektoren und .
Spann
Kann ein Vektor als Linearkombination der Vektoren dargestellt werden, so liegt im Spann der Menge . Diese bezeichnet also all jene Vektoren, die durch Linearkombinationen erzeugt werden können.
Man schreibt: oder
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
