Mögliche Lagebeziehungen zwischen Geraden und Ebenen:
Gerade liegt in Ebene | Jeder Punkt der Gerade liegt in der Ebene, also gibt es unendlich viele Schnittpunkte |  |
|---|---|---|
Gerade und Ebene schneiden sich | Es gibt genau einen Schnittpunkt, den die Ebene und die Gerade gemeinsam haben. | 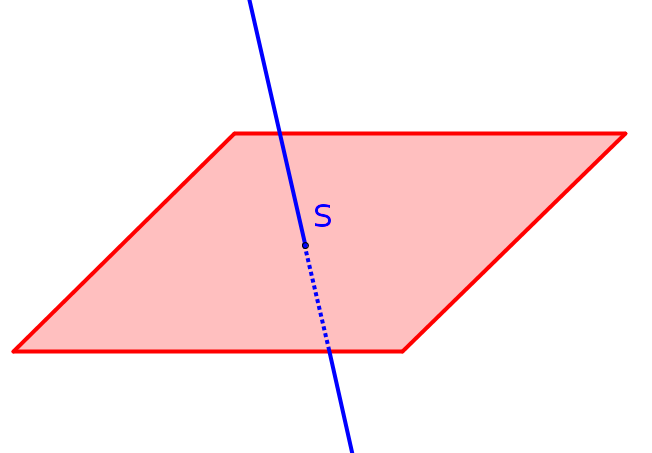 |
Gerade und Ebene echt parallel | Gerade und Ebene besitzen keine gemeinsamen Punkte, insbesondere auch keinen Schnittpunkt |  |
Orientierung bestimmen (analytische Geometrie)
Um den Schnittpunkt zwischen Gerade und Ebene oder die Lagebeziehung zwischen Gerade und Ebene zu berechnen, benötigst du eine Ebene in Koordinatenform und eine Gerade in Parameterform. Falls die Ebene in Parameterform gegeben ist, so formst du diese zuerst in Koordinatenform um. Anschließend kannst du wie folgt vorgehen:
Setze die rechte Seite der Geradengleichung in die Koordinatenform der Ebene ein.
Versuche (allg. den Parameter der Geradengleichung) zu bestimmen.
Aus dem Ergebnis der Gleichung folgt, welcher der oberen 3 Fälle vorliegt.
Ist das Ergebnis:
für alle erfüllt, z.B. bei so liegt die Gerade in der Ebene, und alle Punkte der Geraden liegen auch in der Ebene
für kein erfüllt, z.B. bei so sind Gerade und Ebene echt parallel und haben keinen gemeinsamen Punkt
für genau ein erfüllt, z.B. bei so schneiden sich Gerade und Ebene in genau einem Punkt. Dieser Schnittpunkt lässt sich berechnen, indem man den Wert von in die Geradengleichung einsetzt.
Beispiel:
Sei und
Nun setzt du in ein und versuchst zu bestimmen:
Offensichtlich ist die Gleichung für genau ein erfüllt. Folglich schneiden sich die Gerade und die Ebene in genau einem Punkt. Diesen Schnittpunkt S kannst du nun bestimmen, indem du in die Geradengleichung einsetzt:
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
