Als Radius bezeichnet man den Abstand vom Kreis- oder Kugelmittelpunkt zu einem beliebigen Punkt auf der Kreislinie oder der Kugeloberfläche.
Der doppelte Radius ist der Durchmesser .
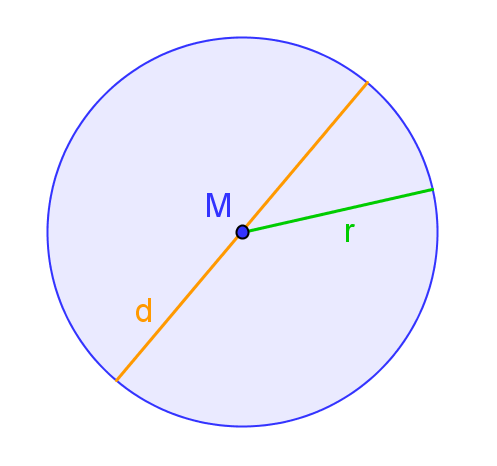
Bestimmung des Radius im Kreis
Hat man den Radius gegeben, berechnet man den Flächeninhalt des Kreises mit der Formel
und den Umfang mit
Ist der Radius unbekannt, aber die Fläche oder der Umfang gegeben, kann man diese Formeln umformen, um zu bestimmen.
Berechnung von bei gegebenen
| ↓ | Löse nach auf. | ||
| ↓ | Ziehe die Wurzel. Da der Radius nicht negativ sein kann, gib nur die positive Lösung an. | ||
Berechnung von bei gegebenen
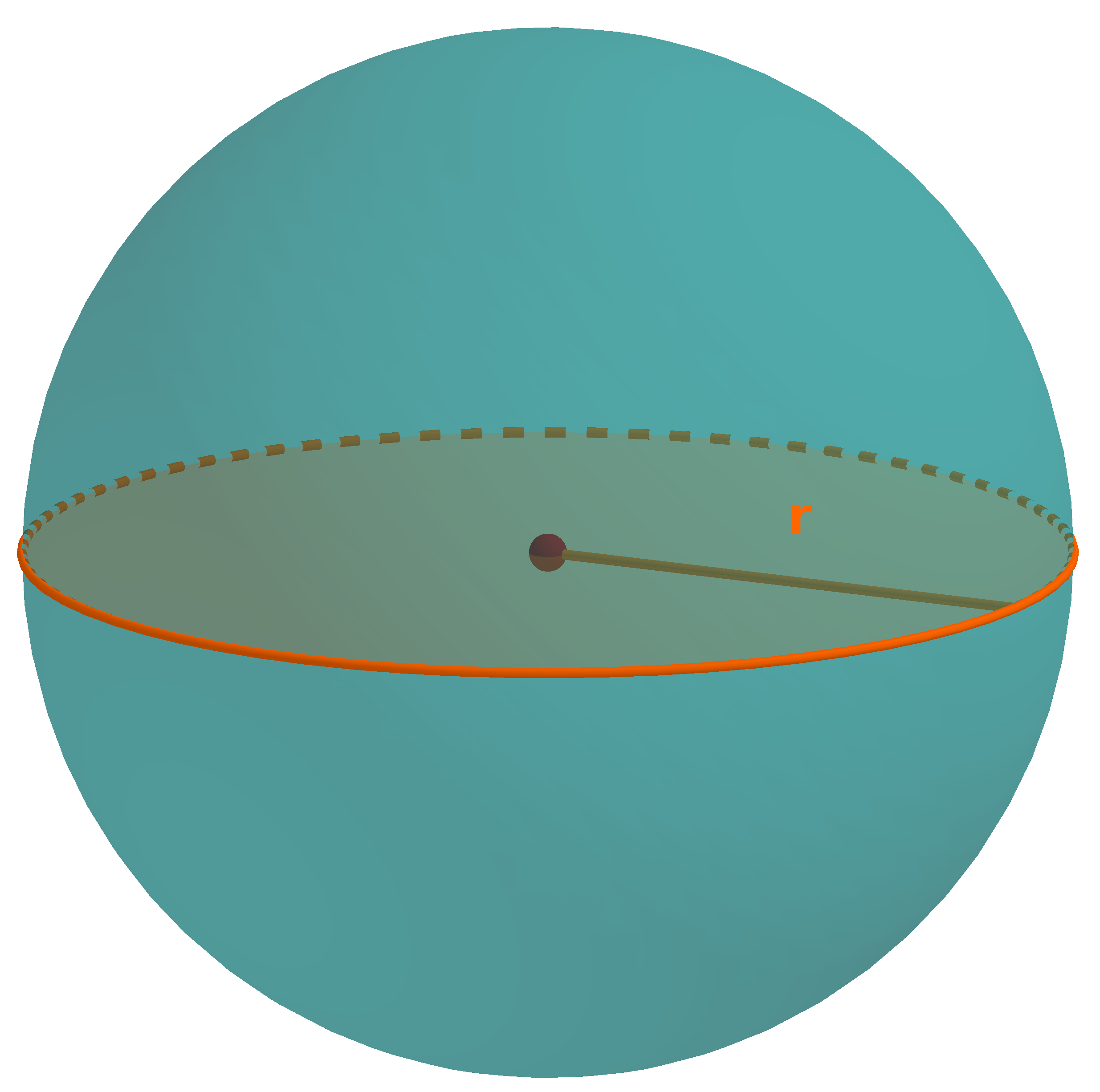
Bestimmung des Radius in der Kugel
Hat man den Radius gegeben, berechnet man das Volumen mit der Formel
und die Oberfläche mit
Ist der Radius unbekannt, aber das Volumen oder die Oberfläche gegeben, kann man diese Formeln umformen, um zu bestimmen.
Berechnung von bei gegebenem
| ↓ | Löse nach auf. | ||
| ↓ | Multipliziere mit dem Kehrbruch. | ||
| ↓ | Vereinfache. Durch Kürzen bekommst du . | ||
Berechnung von bei gegebenen
| ↓ | Löse nach auf. | ||
| ↓ | Ziehe die Wurzel. Da der Radius nicht negativ sein kann, gib nur die positive Lösung an. | ||
Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Kreisen und Kreisteilen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
