Aufgaben zum Bestimmen des Abstands eines Punktes zu einer Geraden
Hier findest du Aufgaben zum Bestimmen des Abstands von Punkt und Geraden mithilfe von Senkrechten.
- 1
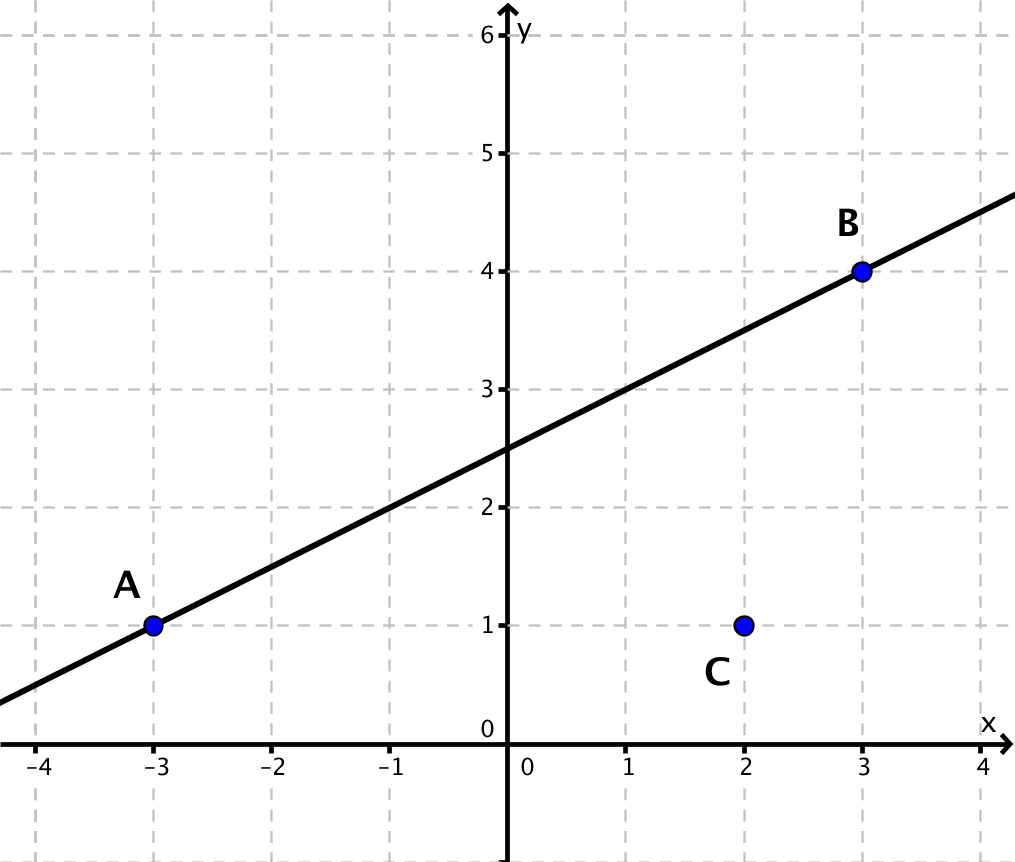
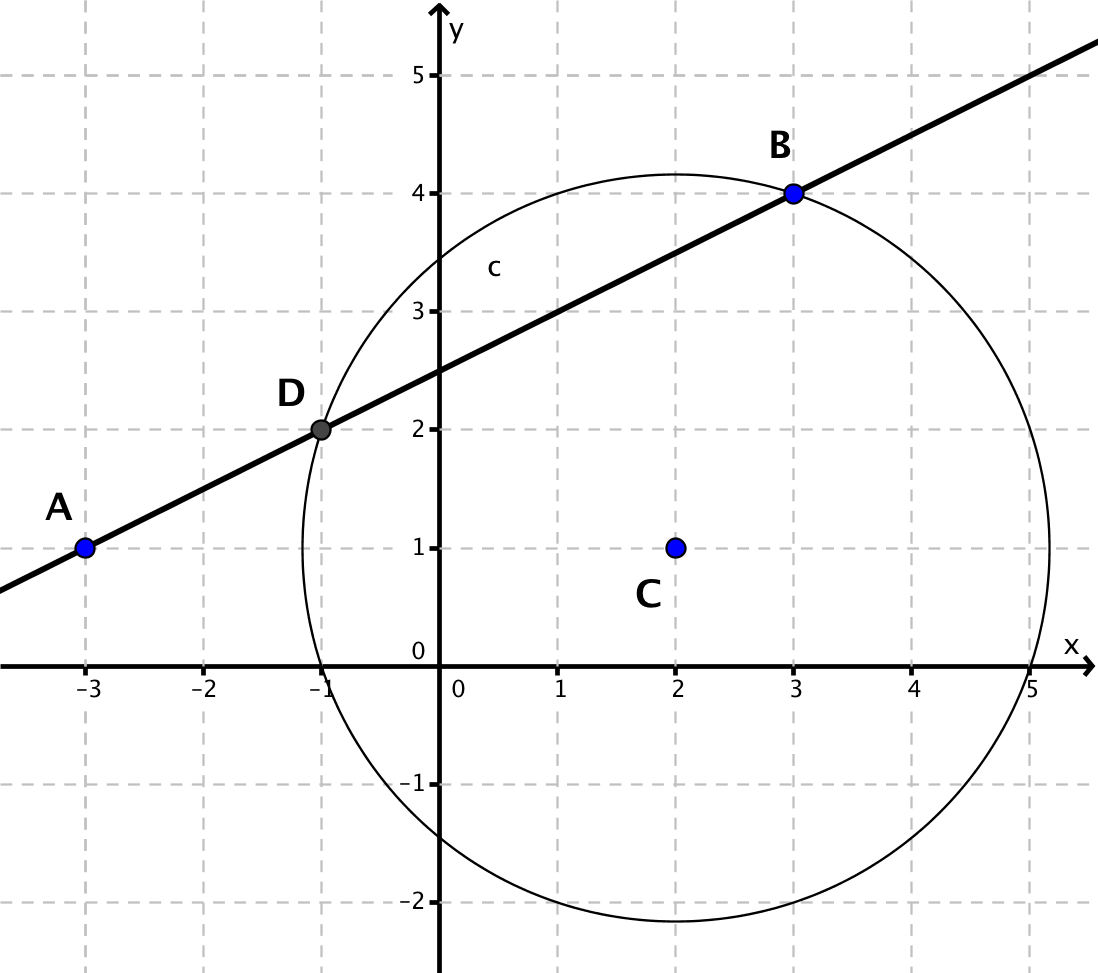
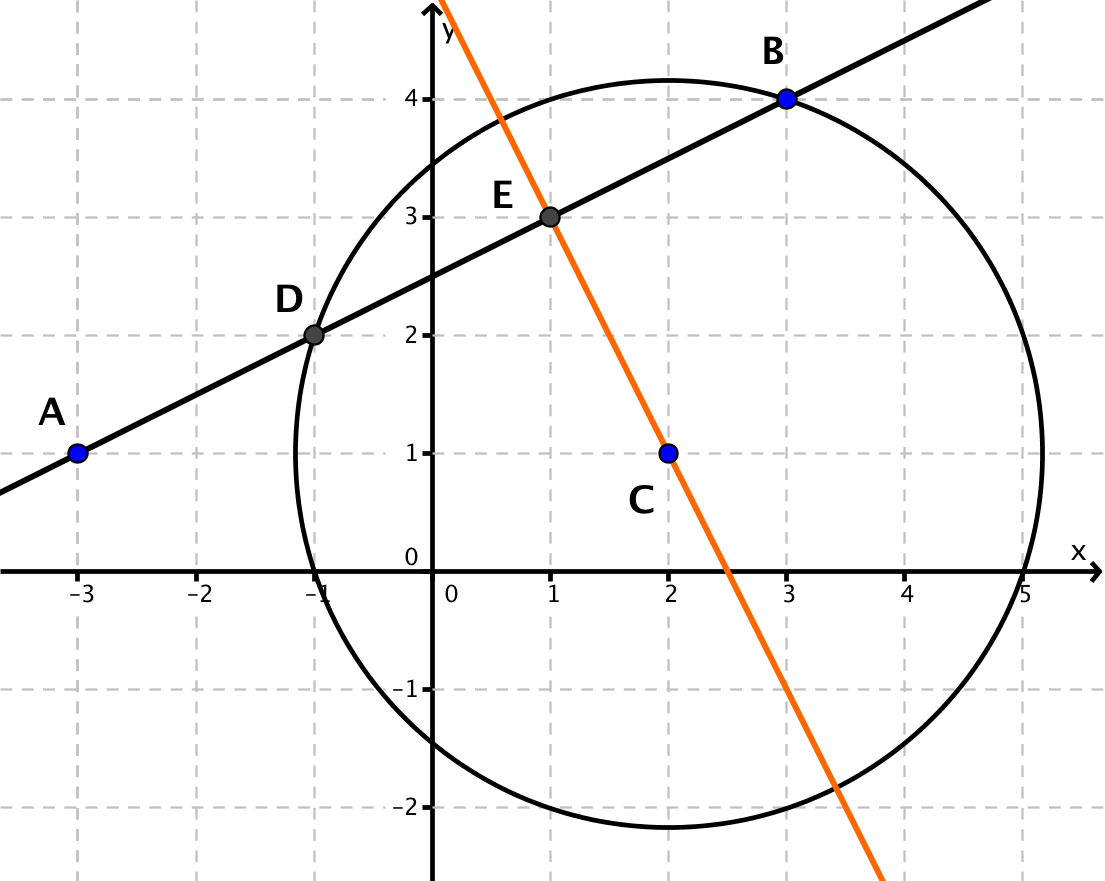
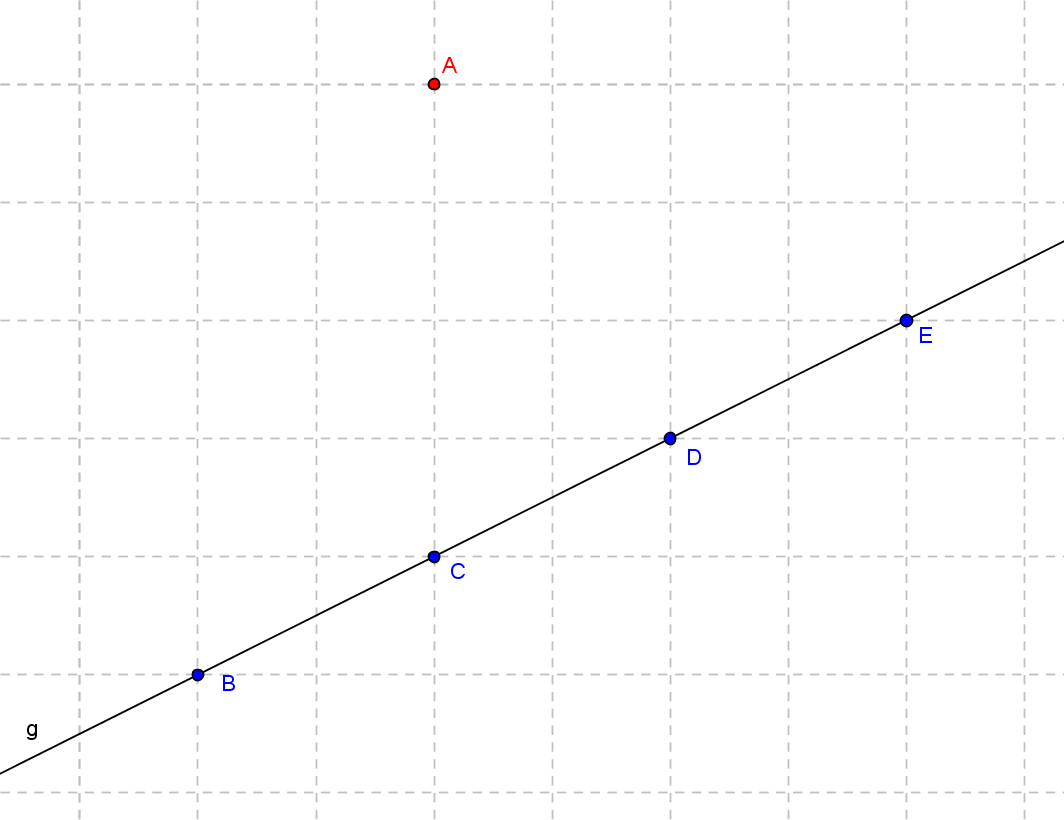
Gegeben sind die Punkte A(2|6), B(0|1), C(2|2), D(4|3) und E(6|4). Die Gerade g verläuft durch die Punkte B bis E. Übertrage nachstehende Skizze in dein Heft und ermittle den Abstand des Punktes A zu den Punkten B, C, D und E sowie zur Geraden g. Halte deine Ergebnisse in einer Tabelle fest. Was weißt du über den Abstand eines Punktes von einer Geraden?
- 2
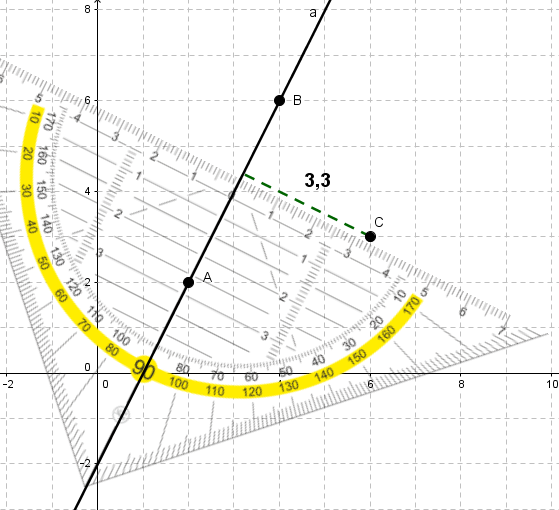
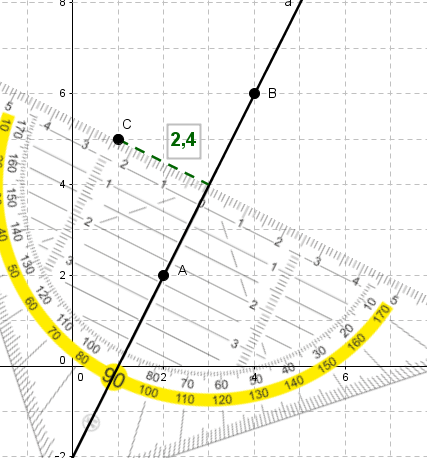
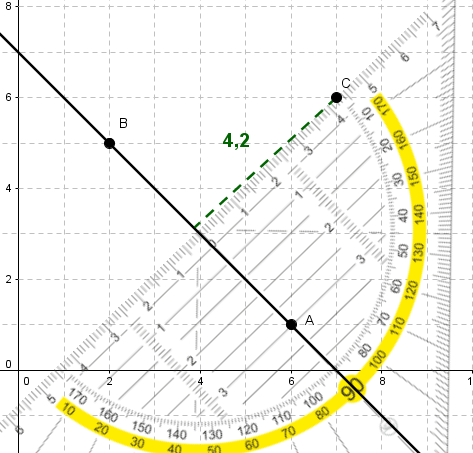
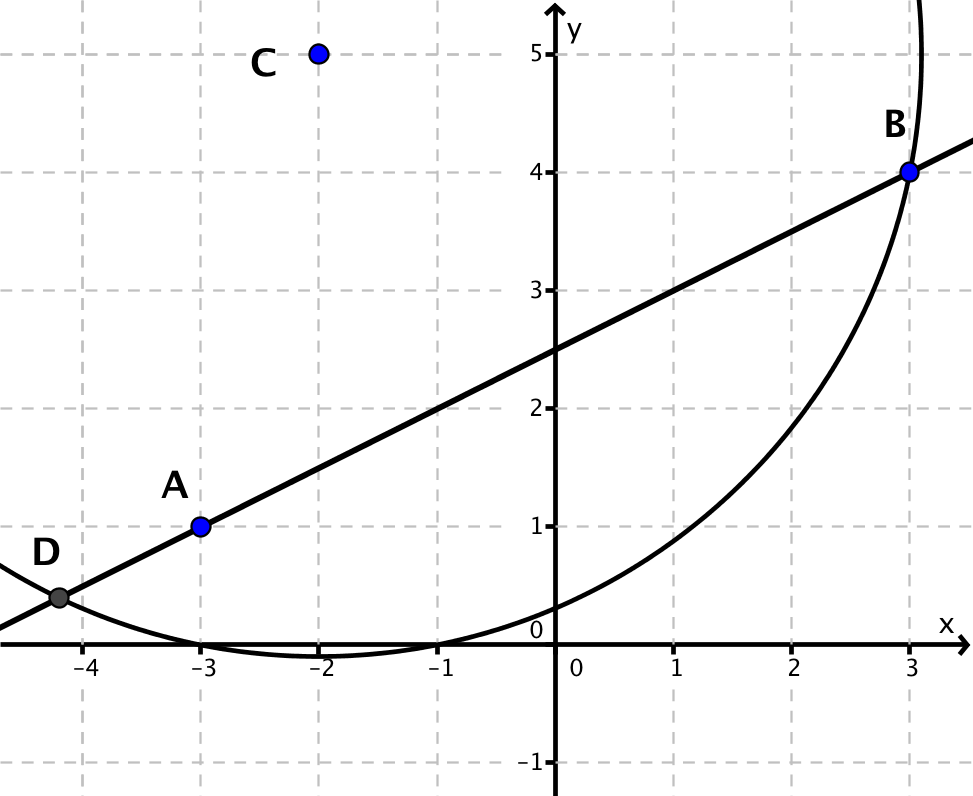
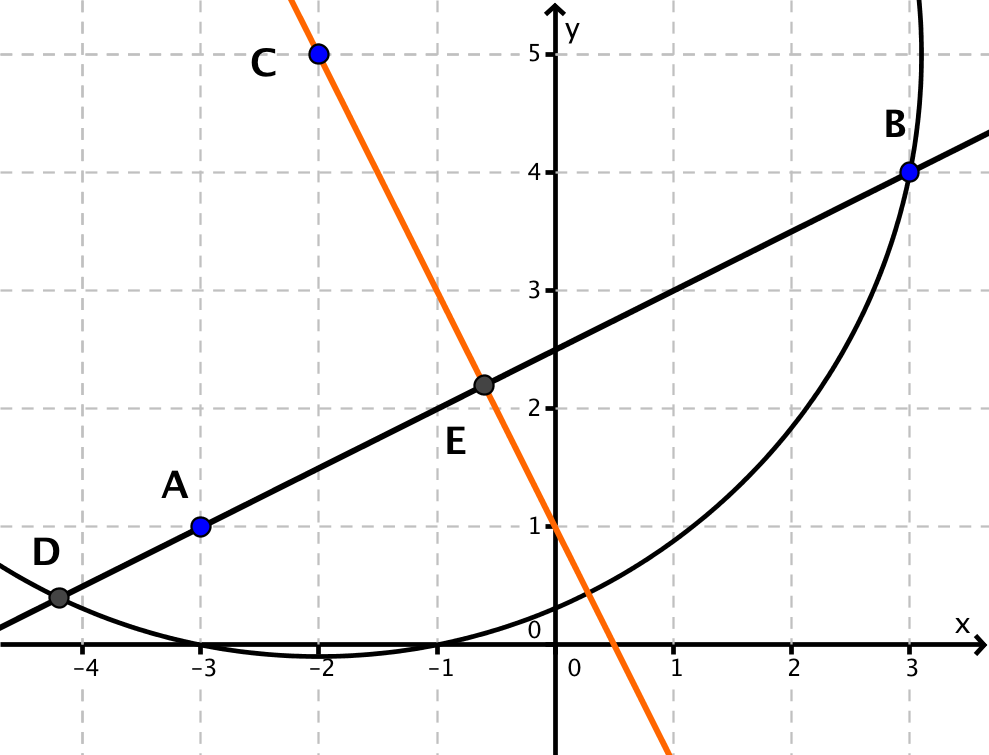
Zeichne die Gerade und den Punkt in ein Koordinatensystem ein und miss den Abstand mit einem Geodreieck.
, ,
, ,
, ,
- 3
Bestimme den Abstand der Gerade zu dem Punkt .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?