Das Bogenmaß ist ein Winkelmaß. Man kann einen bestimmten Winkel sowohl in Bogenmaß als auch in Gradmaß angeben. Folgende Formel gibt die Beziehung zwischen Gradmaß () und Bogenmaß () wieder:
Umrechnungsformeln
Stellt man diese Formel nach dem Bogenmaß um, so erhält man
Damit kann man das Bogenmaß aus dem Gradmaß erhalten. Analog erhält man bei der Umstellung nach dem Gradmaß
Wichtige Werte
Gradmaß | Bogenmaß | Umrechnung |
|---|---|---|
Weitere Werte:
Gradmaß | Bogenmaß |
|---|---|
Beispiel
Geg:
Ges:
Betrachte die Umrechnungformel.
Setze ein.
Erklärung der Definition
Das Bogenmaß ordnet jedem Gradmaß eine eindeutige Zahl zu (mit obiger Umrechnungsformel). Wie ist man auf das Bogenmaß gekommen?
Man kann jeden Winkel auch durch zwei gleichlange Schenkel aufspannen.
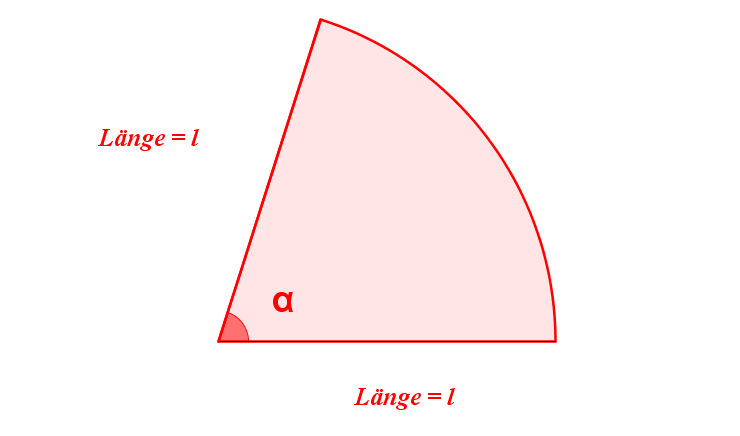
Wähle als Länge , und betrachte die Bogenlänge des Kreissektors.
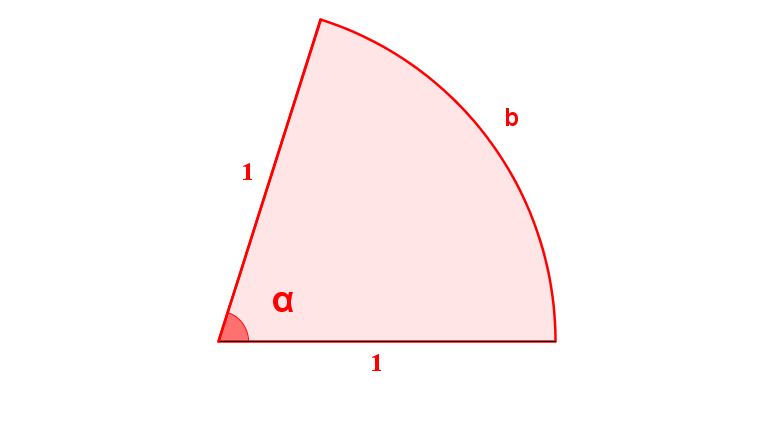
Wie berechnet man ?
Das Bogenmaß eines Winkels ist also die Bogenlänge des Kreissektors mit Radius , der durch den Winkel aufgespannt wird. Man verwendet dafür auch die Pseudoeinheit ("Pseudo" deswegen, weil es keine physikalische Größe wie z.B. der Meter, das Gewicht oder die Geschwindigkeit ist). Allgemein beschreibt den Winkel in einem Kreis mit Radius , der einen Kreisbogen der Länge einschließt. Demnach hat jeder Vollkreis einen Winkel . Dies zeigt auch die folgende Animation.

Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Bogenmaß
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
