Ein Zylinder ist ein dreidimensionaler Körper mit
einem Kreis als Grundfläche,
parallelen Begrenzungslinien
und einem gleich großen Kreis als Deckfläche.
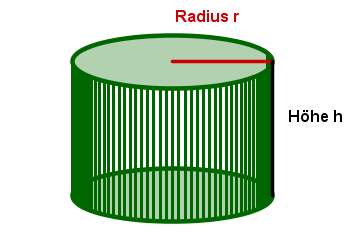
Skizze eines Zylinders
Wichtige Formeln für den Zylinder (Übersicht)
Gesuchte Größe | Formel |
|---|---|
Volumen | |
Oberfläche | |
Mantelfläche |
(Genaueres dazu siehe unten).
Beispiele für Zylinder in der realen Welt
Viele Gegenstände haben als Grundform ungefähr Zylinderform.
Konservendosen haben die Form eines Zylinders.
Dieses Saftglas hat zylinderförmige Gestalt.
Dieser Mülleimer hat Zylinderform.
Auch in der Natur gibt Objekte, die annähernd zylinderförmig sind.

Unverzweigt gewachsene Baumstämme sind ungefähr zylinderförmig.
Begriff Zylinder im Alltag
Wenn außerhalb der Mathematik von Zylindern die Rede ist, steckt oft etwas zylinderförmiges dahinter.
Zylinder beim Auto
Beim Auto bezeichnet man die Teile des Motors, in denen sich die Kolben bewegen, als Zylinder.

Zylinder Hüte
Früher waren Zylinder Hüte eine Weile sehr in Mode. Heute kannst du sie vielleicht noch im Zirkus sehen.

Volumen
: Grundfläche des Zylinders

Oberfläche
: Grundfläche des Zylinders
: Mantelfläche des Zylinders

Video zum Thema Oberfläche und Volumen des Zylinders
Laden
Übungsaufgaben
Laden
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Zylinder
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
