Der Sinus- und der Kosinussatz stellen Beziehungen zwischen Seitenlängen und Winkeln in beliebigen Dreiecken her.
Für ein beliebiges Dreieck mit den Seiten a a a b b b c c c α \alpha α β \beta β γ \gamma γ
Sinussatz
a sin ( α ) = b sin ( β ) = c sin ( γ ) . \displaystyle \frac{a}{\sin\left(\alpha\right)}=\frac{b}{\sin\left(\beta\right)}=\frac{c}{\sin\left(\gamma\right)}._{ }^{ } sin ( α ) a = sin ( β ) b = sin ( γ ) c .
Kosinussatz
c 2 = a 2 + b 2 − 2 a b ⋅ cos ( γ ) c^2=a^2+b^2-2ab\cdot\cos\left(\gamma\right) c 2 = a 2 + b 2 − 2 ab ⋅ cos ( γ )
b 2 = a 2 + c 2 − 2 a c ⋅ cos ( β ) b^2=a^2+c^2-2ac\cdot\cos\left(\beta\right) b 2 = a 2 + c 2 − 2 a c ⋅ cos ( β )
a 2 = b 2 + c 2 − 2 b c ⋅ cos ( α ) a^2=b^2+c^2-2bc\cdot\cos\left(\alpha\right) a 2 = b 2 + c 2 − 2 b c ⋅ cos ( α )
Wenn du den Winkel berechnen willst, musst du nach den Kosinuswerten umformen:
cos ( γ ) = a 2 + b 2 − c 2 2 a b \cos(\gamma)=\dfrac{a^2+b^2-c^2}{2ab} cos ( γ ) = 2 ab a 2 + b 2 − c 2 γ = cos − 1 ( a 2 + b 2 − c 2 2 a b ) \gamma=\cos^{-1}\left(\dfrac{a^2+b^2-c^2}{2ab}\right) γ = cos − 1 ( 2 ab a 2 + b 2 − c 2 )
cos ( β ) = a 2 + c 2 − b 2 2 a c \cos(\beta)=\dfrac{a^2+c^2-b^2}{2ac} cos ( β ) = 2 a c a 2 + c 2 − b 2 β = cos − 1 ( a 2 + c 2 − b 2 2 a c ) \beta=\cos^{-1}\left(\dfrac{a^2+c^2-b^2}{2ac}\right) β = cos − 1 ( 2 a c a 2 + c 2 − b 2 )
cos ( α ) = b 2 + c 2 − a 2 2 b c \cos(\alpha)=\dfrac{b^2+c^2-a^2}{2bc} cos ( α ) = 2 b c b 2 + c 2 − a 2 α = cos − 1 ( b 2 + c 2 − a 2 2 b c ) \alpha=\cos^{-1}\left(\dfrac{b^2+c^2-a^2}{2bc}\right) α = cos − 1 ( 2 b c b 2 + c 2 − a 2 )
▸ Wie stellt man die Formeln um?
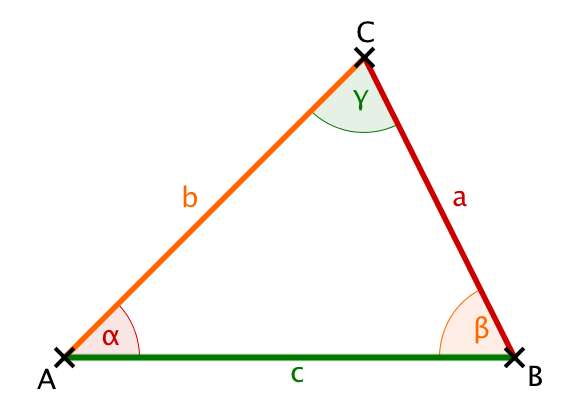
Alternative Formulierung des Sinussatzes Durch Umformungen kann man den Sinussatz auch auf folgende Formen bringen:
sin ( α ) a = sin ( β ) b = sin ( γ ) c . \displaystyle \frac{\sin\left(\alpha\right)}{a}=\frac{\sin\left(\beta\right)}{b}=\frac{\sin\left(\gamma\right)}{c}. a sin ( α ) = b sin ( β ) = c sin ( γ ) .
a b = sin ( α ) sin ( β ) a c = sin ( α ) sin ( γ ) b c = sin ( β ) sin ( γ ) \displaystyle \frac{a}{b}=\frac{\sin\left(\alpha\right)}{\sin\left(\beta\right)}\qquad\qquad\qquad
\frac{a}{c}=\frac{\sin\left(\alpha\right)}{\sin\left(\gamma\right)}\qquad\qquad\qquad\frac{b}{c}=\frac{\sin\left(\beta\right)}{\sin\left(\gamma\right)}
b a = sin ( β ) sin ( α ) c a = sin ( γ ) sin ( α ) c b = sin ( γ ) sin ( β )
Man kann nach den einzelnen Größen auflösen:
a = b sin ( β ) ⋅ sin ( α ) = c sin ( γ ) ⋅ sin ( α ) \displaystyle a=\frac{b}{\sin(\beta)}\cdot \sin(\alpha)
=\frac{c}{\sin(\gamma)}\cdot \sin(\alpha) a = sin ( β ) b ⋅ sin ( α ) = sin ( γ ) c ⋅ sin ( α )
b = a sin ( α ) ⋅ sin ( β ) = c sin ( γ ) ⋅ sin ( β ) \displaystyle b=\frac{a}{\sin(\alpha)}\cdot \sin(\beta)
=\frac{c}{\sin(\gamma)}\cdot \sin(\beta) b = sin ( α ) a ⋅ sin ( β ) = sin ( γ ) c ⋅ sin ( β )
c = a sin ( α ) ⋅ sin ( γ ) = b sin ( β ) ⋅ sin ( γ ) \displaystyle c=\frac{a}{\sin(\alpha)}\cdot \sin(\gamma)
=\frac{b}{\sin(\beta)}\cdot \sin(\gamma) c = sin ( α ) a ⋅ sin ( γ ) = sin ( β ) b ⋅ sin ( γ )
Auflösung nach den Winkeln:
α = sin − 1 ( a b sin ( β ) ) = sin − 1 ( a c sin ( γ ) ) \displaystyle \alpha=\sin^{-1}\left(\frac{a}{b}\sin(\beta)\right)=
\sin^{-1}\left(\frac{a}{c}\sin(\gamma)\right) α = sin − 1 ( b a sin ( β ) ) = sin − 1 ( c a sin ( γ ) ) β = sin − 1 ( b a sin ( α ) ) = sin − 1 ( b c sin ( γ ) ) \displaystyle \beta=
\sin^{-1}\left(\frac{b}{a}\sin(\alpha)\right)=
\sin^{-1}\left(\frac{b}{c}\sin(\gamma)\right) β = sin − 1 ( a b sin ( α ) ) = sin − 1 ( c b sin ( γ ) ) γ = sin − 1 ( c a sin ( α ) ) = sin − 1 ( c b sin ( β ) ) \displaystyle \gamma=\sin^{-1}\left(\frac{c}{a}\sin(\alpha)\right)=
\sin^{-1}\left(\frac{c}{b}\sin(\beta)\right) γ = sin − 1 ( a c sin ( α ) ) = sin − 1 ( b c sin ( β ) )
Wenn du aus einem Sinuswert in einem Dreieck den Winkel berechnen willst, beachte, dass die Gleichung sin ( α ) = x \sin(\alpha)=x sin ( α ) = x 0 ∘ 0^\circ 0 ∘ 18 0 ∘ 180^\circ 18 0 ∘ zwei Lösungen hat:
mit dem α \alpha α sin − 1 ( x ) \sin^{-1}(x) sin − 1 ( x ) 18 0 ∘ − α 180^\circ-\alpha 18 0 ∘ − α
Der Satz des Pythagoras als Spezialfall des Kosinussatzes Für γ = 9 0 ∘ \gamma=90^\circ γ = 9 0 ∘ cos ( 9 0 ∘ ) = 0 \cos(90^\circ)=0 cos ( 9 0 ∘ ) = 0 Satz des Pythagoras c 2 = a 2 + b 2 c^2=a^2+b^2 c 2 = a 2 + b 2
Beispiel Im Dreieck A B C ABC A BC a = 6 , 10 a=6{,}10 a = 6 , 10 α = 4 5 ∘ \mathrm\alpha=45^\circ α = 4 5 ∘ β = 5 5 ∘ \beta=55^\circ β = 5 5 ∘ γ = 8 0 ∘ \gamma=80^\circ γ = 8 0 ∘
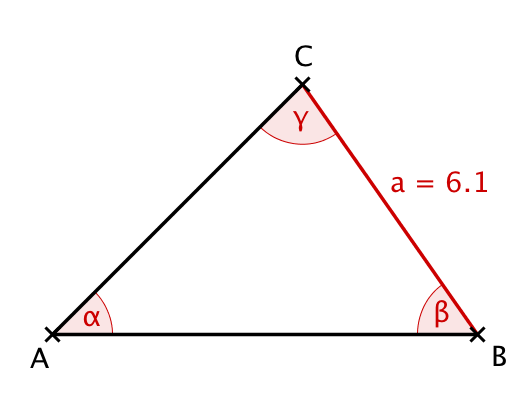
Berechne zuerst mithilfe des Sinussatzes die Länge der Seite b b b
a sin ( α ) = b sin ( β ) \displaystyle \frac{a}{\sin(\alpha)}=\frac{b}{\sin\left(\beta\right)} sin ( α ) a = sin ( β ) b Setze die bekannten Werte ein.
6 , 1 sin ( 4 5 ∘ ) = b sin ( 5 5 ∘ ) \displaystyle \frac{6{,}1}{\sin\left(45^{\circ}\right)}=\frac{b}{\sin\left(55^{\circ}\right)} sin ( 4 5 ∘ ) 6 , 1 = sin ( 5 5 ∘ ) b ⇒ b = 6 , 1 ⋅ sin ( 5 5 ∘ ) sin ( 4 5 ∘ ) = 7 , 1 \displaystyle \Rightarrow b=\frac{6{,}1\cdot\sin(55^{\circ})}{\sin(45^{\circ})}=7{,}1 ⇒ b = sin ( 4 5 ∘ ) 6 , 1 ⋅ sin ( 5 5 ∘ ) = 7 , 1 Berechne nun mithilfe des Kosinussatzes die Länge der Seite c c c
c = a 2 + b 2 − 2 a b ⋅ cos ( γ ) \displaystyle c=\sqrt{a^2+b^2-2ab\cdot\cos\left(\gamma\right)} c = a 2 + b 2 − 2 ab ⋅ cos ( γ ) = 6 , 1 2 + 7 , 1 2 − 2 ⋅ 6 , 1 ⋅ 7 , 1 ⋅ cos ( 8 0 ∘ ) = 8 , 5 \displaystyle =\sqrt{6{,}1^2+7{,}1^2-2\cdot6{,}1\cdot7{,}1\cdot\cos\left(80^{\circ}\right)}=8{,}5 = 6 , 1 2 + 7 , 1 2 − 2 ⋅ 6 , 1 ⋅ 7 , 1 ⋅ cos ( 8 0 ∘ ) = 8 , 5
Video Übungsaufgaben: Sinussatz und Kosinussatz im allgemeinen Dreieck Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:Aufgaben zu Sinussatz und Kosinussatz
