Aufgaben zum Sinus und Kosinus am Einheitskreis

Wie gut kennst du dich aus? Hier findest du Aufgaben zum Sinus und Kosinus am Einheitskreis.

1
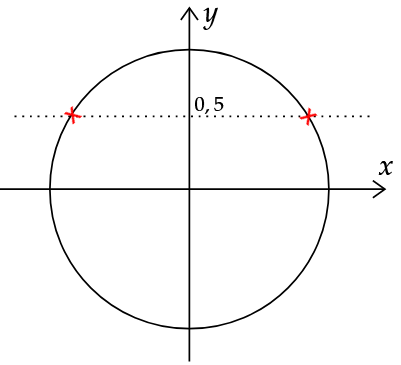
Überlege am Einheitskreis: Für welche Winkel zwischen $0^\circ$ und $360^\circ$ gilt $\sin\left(\alpha\right)=0{,}5$ ?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Einheitskreis
Verwende eine Skizze des Einheitskreises und zeichne eine Hilfslinie bei $y=0{,}5$ .
Markiere die Schnittpunkte der Hilfslinie mit dem Kreis.
Miss die Winkel zwischen der x-Achse und den Schenkeln, die zu diesen Schnittpunkten führen.
Das sind die gesuchten Winkel.
Für die Winkel $30°$ und $150°$ gilt : $\ \text{sin}(\alpha)=0{,}5$
2
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
Bestimmen Sie alle Lösungen der folgenden Gleichungen im Bereich $\gamma\in\left[-180^\circ;720^\circ\right]$ ( Teilaufgabe (a) ) bzw. $x\in\left[-2\mathrm\pi;\;6\mathrm\pi\right]$ ( ) (Teilaufgaben (b) - (c) )
1. $\cos\left(\gamma\right)=\frac12\sqrt2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrie am Einheitskreis
  $\cos\left(\gamma\right)=\frac12\sqrt2$
  Der Kosinus ist im ersten sowie im vierten Quadranten positiv.
  1. Winkel
  $\cos\left(\gamma\right)=\frac12\sqrt2$
  $\gamma_1=45^\circ$
  2. Winkel
  $\cos\left(360^\circ-\gamma_1\right)=\frac12\sqrt2$
  $\cos\left(360^\circ-45^\circ\right)=\frac12\sqrt2$
  $\gamma_2=315^\circ$
  3. Winkel
  $\cos\left(360^\circ+\gamma_1\right)=\frac12\sqrt2$
  $\cos\left(360^\circ+45^\circ\right)=\frac12\sqrt2$
  $\gamma_3=405^\circ$
  4. Winkel
  $\cos\left(720^\circ-\gamma_1\right)=\frac12\sqrt2$
  $\cos\left(720^\circ-45^\circ\right)=\frac12\sqrt2$
  $\gamma_3=675^\circ$
  5. Winkel
  $\cos\left(0^\circ-\gamma_1\right)=\frac12\sqrt2$
  $\cos\left(0^\circ-45^\circ\right)=\frac12\sqrt2$
  $\gamma_4=-45^\circ$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $\sin\left(\frac x2\right)=1$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrie am Einheitskreis
  $\sin\left(\frac x2\right)=1$
  Sinus ist im ersten und zweiten Quadranten positiv.
  $y\in\left[-\mathrm\pi;\;3\mathrm\pi\right]$
  1.Winkel im Bogenmaß
  $\dfrac x2=y$
  $\sin\left(y\right)=1$
  $y_1=\dfrac12\mathrm\pi$
  $x_1=\mathrm\pi$
  2. Winkel im Bogenmaß
  $\sin\left(2\mathrm\pi+y_1\right)=1$
  $\sin\left(2\mathrm\pi+\frac{\mathrm\pi}2\right)=1$
  $\gamma_2=2{,}5\mathrm\pi$
  $x=5\mathrm\pi$
  3. Winkel im Bogenmaß
  $\sin\left(0-y_1\right)=1$
  $\sin\left(-\frac{\mathrm\pi}2\right)=1$
  $y_3=-\frac12\mathrm\pi$
  $x=-\mathrm\pi$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $\sin\left(x\right)=-2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrie am Einheitskreis
  $\sin\left(x\right)=-2$
  Geht nicht, da gilt: $-1\leq\sin\left(x\right)\leq1$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
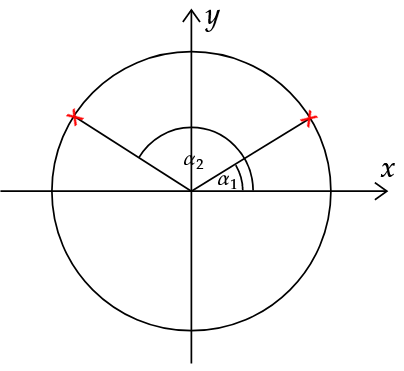
Für welche Winkel $\gamma$ gilt: $\gamma\in\left[0^\circ;\;360^\circ\right]$ und $\cos\left(\gamma\right)=-\sin\left(\gamma\right)$ ?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrie
$\cos\left(\gamma\right)=-\sin\left(\gamma\right)$
Der/Die Winkel müssen im zweiten und vierten Quadranten liegen.
$\sin\left(\gamma\right)=\cos\left(\gamma\right)$ wenn gilt $\gamma=45^\circ$
Dem Winkel $\gamma=45^\circ$ entsprechen
1.Winkel
$Syntax error from line 1 column 323 to line 1 column 328. Unexpected ''.$
$Syntax error from line 1 column 253 to line 1 column 258. Unexpected ''.$
$\gamma=135^\circ$
$-\left(\frac{\sqrt2}2\right)=-\frac{\sqrt2}2$
2.Winkel
$Syntax error from line 1 column 325 to line 1 column 330. Unexpected ''.$
$Syntax error from line 1 column 253 to line 1 column 258. Unexpected ''.$
$\gamma=315^\circ$
$-\left(-\frac{\sqrt2}2\right)=\frac{\sqrt2}2$
$\frac{\sqrt2}2=\frac{\sqrt2}2$

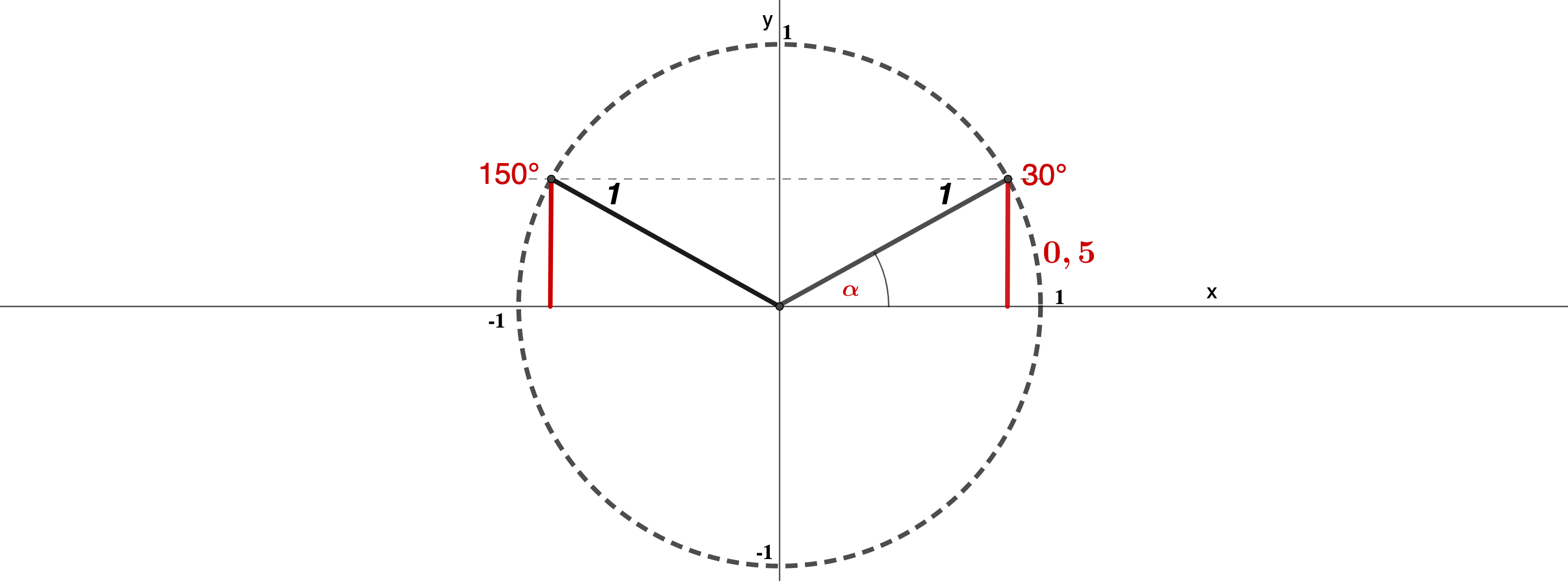
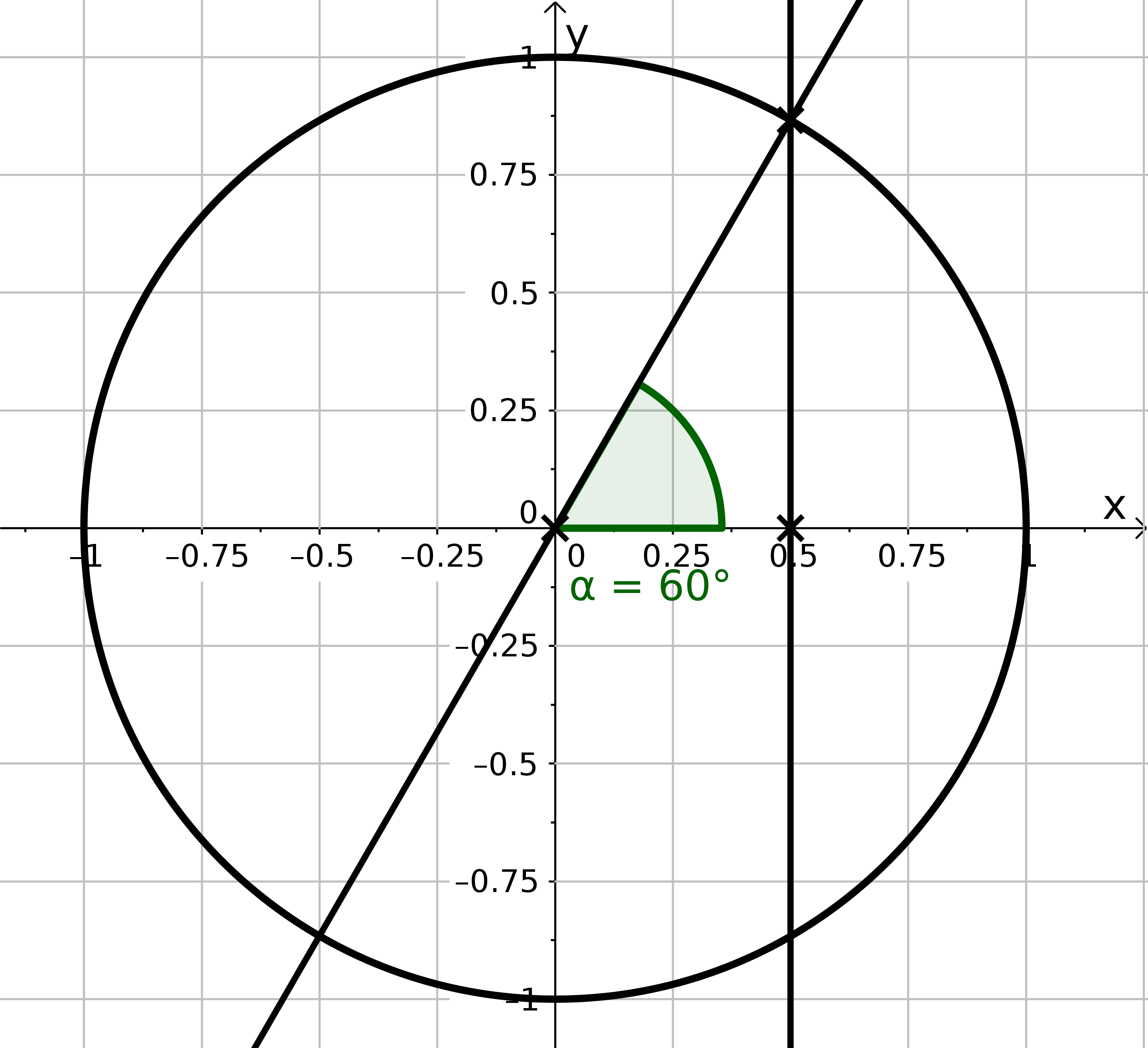
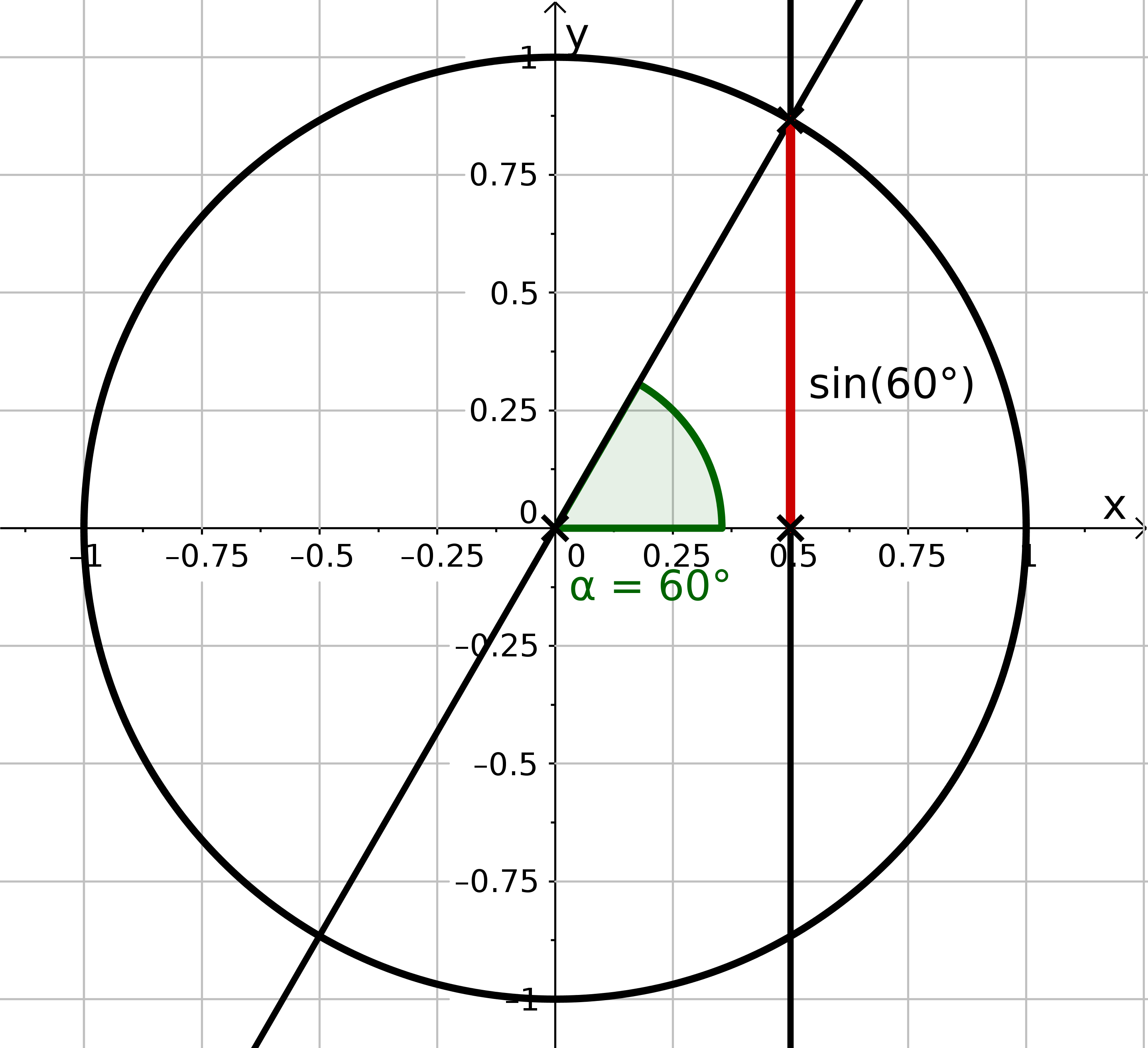
In dieser Aufgabe geht es darum, $\sin(60°)$ zu berechnen.

Zeichne ein großes Koordinatensystem. $(1 \text{ Längeneinheit} \; \hat{=} \; 8 \text{ Kästchen})$ . Konstruiere mit dem Zirkel den Einheitskreis und trage mit dem Geodreieck einen $60°$ -Winkel an die $x$ -Achse. Konstruiere die Länge $\sin(60°)$ und messe sie mit dem Lineal.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrie am Einheitskreis
Zeichne das Koordinatensystem.
Konstruiere den Einheitskreis mit deinem Zirkel.
Benutze das Geodreieck, um einen $60°$ -Winkel an die $x$ -Achse zu zeichnen. Markiere den Schnittpunkt der entstehenden Gerade mit dem Einheitskreis.
Zeichne das Lot, also eine Senkrechte, zur $x$ -Achse, das durch den markierten Punkt verläuft.
Nun kannst du die Länge des Sinus mit deinem Lineal messen.
$\sin(60°) \approx 0{,}87$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

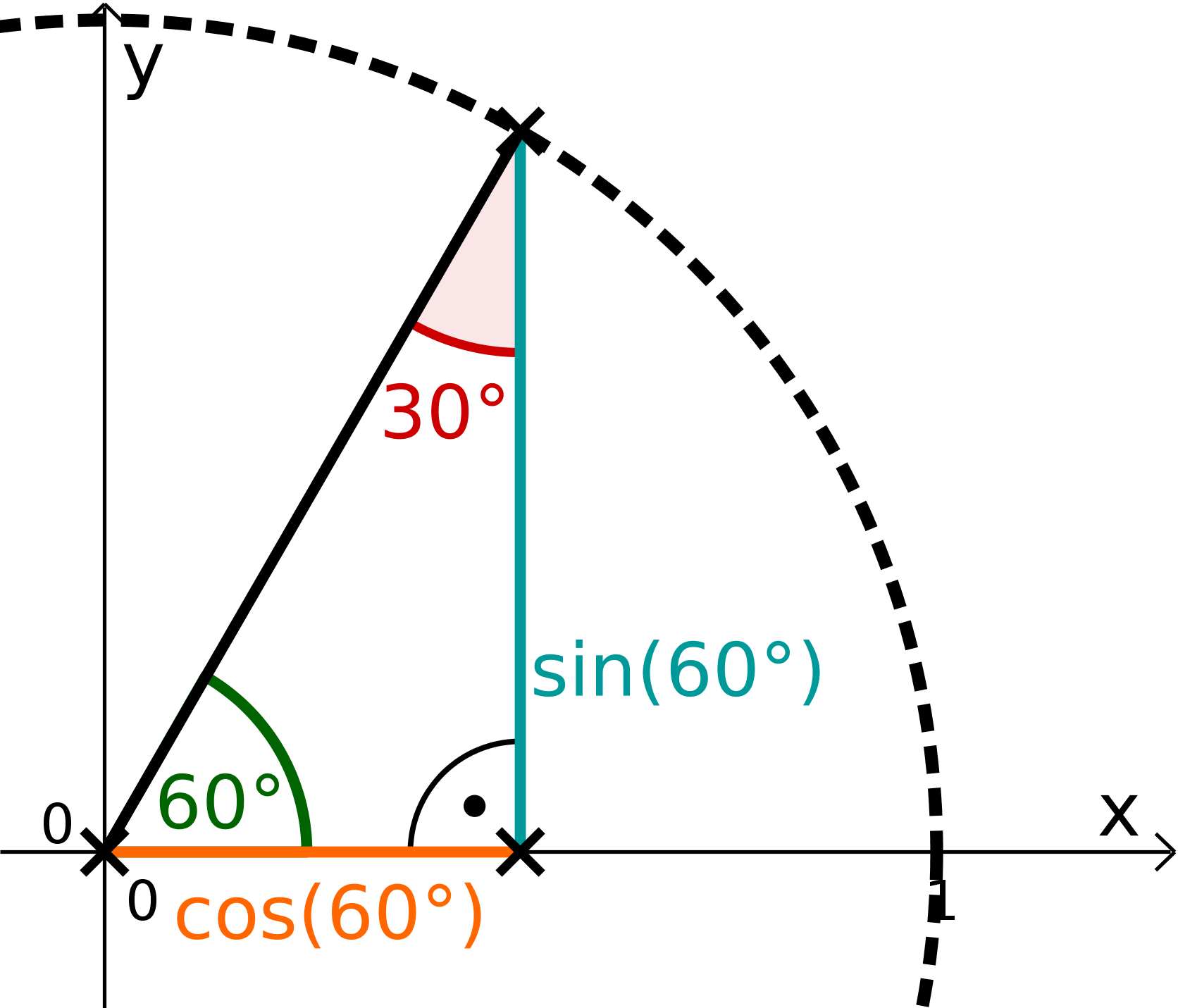
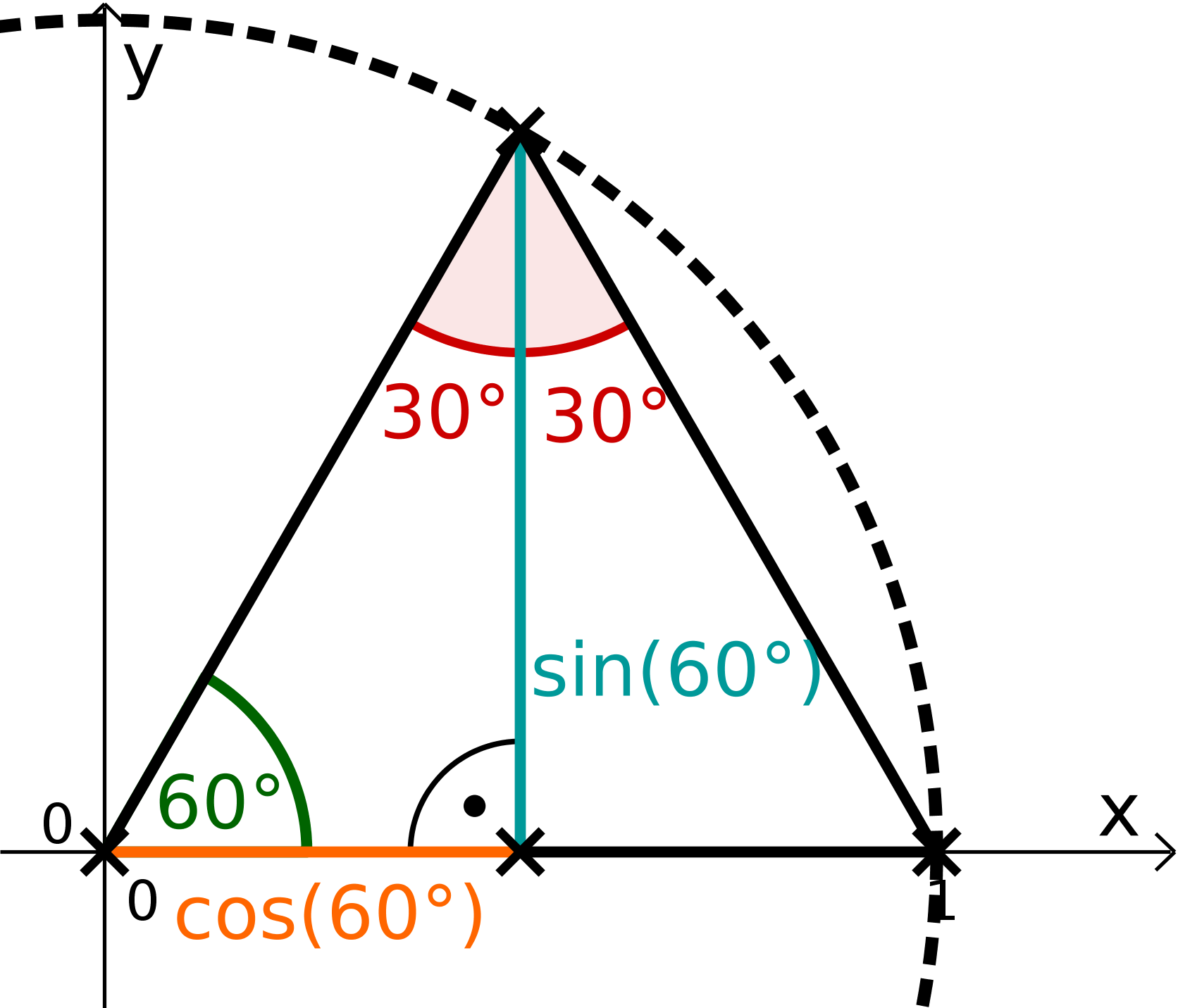
Berechne $\sin(60°)$ genau. Finde dafür zuerst den Wert für $\cos(60°)$ heraus. Konstruiere dafür ein gleichseitiges Dreieck.

5
Gleiche Sinus- und Kosinuswerte
1. Wähle alle Terme aus, die den gleichen Termwert haben wie $\sin\left(30°\right)$ .
  $\sin\left(150°\right)$
  $\sin\left(210°\right)$
  $\sin\left(330°\right)$
  $\sin(120°)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrie am Einheitskreis
  Vorüberlegungen
  Der Winkel 30° liegt im I. Quadranten
  Im II. Quadranten gibt es einen Winkel mit gleichem Sinuswert, die Beziehung lautet $\sin\left(\alpha\right)=\sin\left(180°-\alpha\right)$
  Die Winkel im III. und IV. Quadranten sind betragsgleich, aber nicht wertgleich (negative Werte)
  Durch Addition oder Subtraktion von Vielfachen von 360° können die beiden Lösungen aus dem I. und II. Quadranten für negative Winkelwerte/große Winkelwerte übertragen werden. Die Beziehung lautet $\sin\left(\alpha\right)=\sin\left(\alpha+k\cdot360°\right),\ k\in\mathbb Z$ .
  Analyse der Antwortmöglichkeiten
  $sin(150°)$ : Da $150°=180°-\alpha$ , gilt $\Rightarrow\color{green}{\sin(150°)=\sin(30°)}$
  $sin(210°)$ : Da $210°=180°+30°$ ist der Sinus hier zwar betragsgleich, aber nicht wertgleich, der Sinuswert ist für Winkel im III. Quadranten nämlich negativ. $\Rightarrow\color{red}{sin(210°)=-sin(30°)}$
  $sin(330°)$ : Da $330°=360°-30°$ ist der Sinus hier ebenfalls betragsgleich, aber auch für Winkel im IV. Quadranten ist der Sinuswert negativ. $\Rightarrow\color{red}{sin(330°)=-sin(30°)}$
  $sin(120°)$ : Dieser Winkel liegt zwar im II. Quadranten, aber da $120\neq 180°-30°$ sind die Sinuswerte nicht wertgleich ( $90°+\alpha$ ist keine gültige Beziehung. $\Rightarrow\color{red}{sin(120°)\neq sin(30°)}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Überlege zunächst, in welchem Quadranten der Winkel sich befindet und anschließend, welche Quadranten den gleichen Wert für den Sinus haben.
2. Wähle alle Terme aus, die den gleichen Termwert haben wie $\sin\left(230°\right)$ .
  $\sin\left(310°\right)$
  $-\sin\left(310°\right)$
  $-\sin\left(50°\right)$
  $\sin\left(590°\right)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrie am Einheitskreis
  Vorüberlegungen
  Es ist nützlich, die Winkel, die größer sind als 90° auf einen spitzen Winkel im I. Quadranten zurückzuführen, da die Beziehungsgleichungen für einen Winkel $0°<\alpha<90°$ formuliert sind.
  Der Winkel 230° liegt im III. Quadranten
  Den "zugehörigen" spitzen Winkel $\alpha'$ im I. Quadranten erhält man durch $\alpha'+180°=230\Leftrightarrow \alpha'=230°-180°=50°$
  Im IV. Quadranten gibt es einen Winkel mit gleichem Sinuswert, die Beziehung lautet $\sin\left(\alpha'\right)=\sin\left(360°-\alpha'\right)$
  Die Winkel im I. und II. Quadranten sind betragsgleich, aber nicht wertgleich (positive Werte)
  Durch Addition oder Subtraktion von Vielfachen von 360° können die beiden Lösungen aus dem III. und IV. Quadranten für negative Winkelwerte/große Winkelwerte übertragen werden. Die Beziehung lautet $\sin\left(\alpha\right)=\sin\left(\alpha+k\cdot360°\right),\ k\in\mathbb Z$ .
  Analyse der Antwortmöglichkeiten
  Verwende $\alpha'=50°$ aus den Vorüberlegungen für die Beziehungen, denn $sin(230°)=-sin(50°)$ und die Beziehungsgleichungen sind nur für spitze Winkel.
  $sin(310°)$ : Da $310°$ im IV. Quadranten und $310°=360°-\alpha'=360°-50°$ , gilt $\Rightarrow\color{green}{\sin(230°)=\sin(310°)}$
  $-sin(310°)$ : Da du gerade herausgefunden hast, dass $sin(230°)=sin(310°)$ und gleichzeitig nicht $sin(230°)=0$ , ist die Aussage falsch. $\Rightarrow\color{red}{sin(230°)\neq-sin(310°)}$
  $-sin(50°)$ : Da $50°$ im I. Quadranten liegt und $230°=180°+50°$ ist der Sinus hier nur betragsgleich, nicht wertgleich. Durch das Minus vor dem Term wird er wertgleich. $\Rightarrow\color{green}{sin(230°)=-sin(50°)}$
  $sin(590°)$ : Da $590°=1\cdot360°+230°$ ist der Winkel an der gleichen Stelle einzutragen, nur eine Umrundung später. Der Sinus ist für diesen Winkel also wertgleich . $\Rightarrow\color{green}{sin(590°)= sin(230°)}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Überlege zunächst, in welchem Quadranten der Winkel sich befindet und anschließend, welche Quadranten den gleichen Wert für den Sinus haben.
3. Wähle alle Terme aus, die den gleichen Termwert haben wie $\sin\left(90°\right)$ .
  $\sin\left(270°\right)$
  $\sin\left(360°\right)$
  $\sin\left(180°\right)$
  $\sin\left(-270°\right)$
  $\sin\left(450°\right)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrie am Einheitskreis
  Vorüberlegungen
  Da der Sinus dem y-Wert des Punktes auf dem Einheitskreis entspricht, ist der Winkel $\alpha=90°$ genau die y-Achse.
  Der Sinus ist hier maximal und hat den Wert $sin(90°)=1$ .
  Es gibt keinen weiteren Winkel in $[0°;360°]$ , der den gleichen Sinuswert hat.
  Betragsgleich ist $sin(270°)=-1$
  Durch Addition oder Subtraktion von Vielfachen von 360° kann die Lösung für negative Winkelwerte/große Winkelwerte übertragen werden. Die Beziehung lautet $\sin\left(\alpha\right)=\sin\left(\alpha+k\cdot360°\right),\ k\in\mathbb Z$
  Analyse der Antwortmöglichkeiten
  $sin(270°)$ : wie in den Vorüberlegungen beschrieben ist diese Lösung nur betragsgleich, nicht wertgleich $\Rightarrow\color{red}{\sin(90°)=-\sin(270°)\neq sin(270°)}$
  $sin(360°)$ : Da der Sinuswert der y-Koordinate des Punktes auf dem Einheitskreis beim Winkel entspricht und 360° der Vollkreis ist, ist der Punkt auf der x-Achse und die y-Koordinate ist 0 $\Rightarrow\color{red}{sin(90°)\neq sin(360°)}$
  $sin(180°)$ : Ähnlich zu 360° ist auch hier die y-Koordinate 0 $\Rightarrow\color{red}{sin(90°)\neq sin(180°)}$
  $sin(-270°)$ : Da $-270°=90°-360°$ befindest du dich hier am gleichen Punkt im Einheitskreis $\Rightarrow\color{green}{sin(90°)= sin(-270°)}$
  $sin(450°)$ : Da $450°=1\cdot 360°+90°$ befindest du dich hier am gleichen Punkt im Einheitskreis $\Rightarrow \color{green}{sin(90°)=sin(450°)}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Überlege zunächst, in welchem Quadranten der Winkel sich befindet und anschließend, welche Quadranten den gleichen Wert für den Sinus haben.
4. Wähle alle Terme aus, die den gleichen Termwert haben wie $\cos\left(300°\right)$ .
  $\cos\left(60°\right)$
  $\cos\left(120°\right)$
  $\cos\left(240°\right)$
  $\cos\left(-60°\right)$
  $-\cos\left(60°\right)$
  $\cos\left(-300°\right)$
5. Wähle alle Terme aus, die den gleichen Termwert haben wie $\cos\left(0°\right)$ .
  $\cos\left(90°\right)$
  $\cos\left(180°\right)$
  $\cos\left(270°\right)$
  $\cos\left(360°\right)$
  $\cos\left(-720°\right)$
  $\cos\left(-1080°\right)$
6. Wähle alle Terme aus, die den gleichen Termwert haben wie $\sin\left(1520°\right)$ .
  $\sin\left(100°\right)$
  $\sin\left(660°\right)$
  $\sin\left(-80°\right)$
  $\sin\left(80°\right)$
  $\sin\left(2600°\right)$
7. Wähle alle Terme aus, die den gleichen Termwert haben wie $\cos\left(-130°\right)$ .
  $\cos\left(230°\right)$
  $\cos\left(-230°\right)$
  $\cos\left(50°\right)$
  $\cos\left(-50°\right)$
  $\cos\left(-1210°\right)$
6
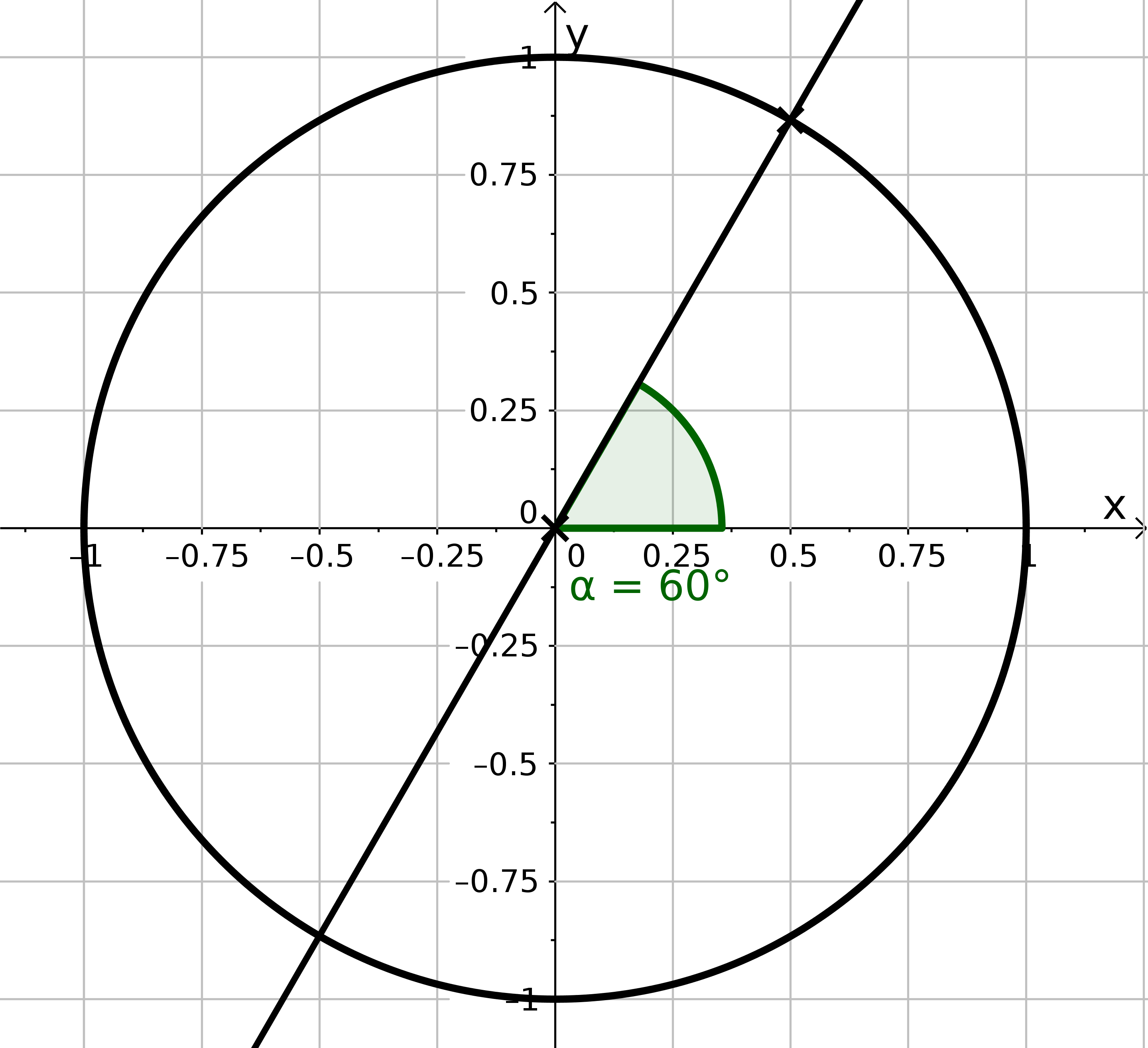
Bestimme alle Werte $\alpha\in\left[-360°;720°\right]$ für die die Gleichung erfüllt ist. Gib die Werte einzeln und auf ganze Grad gerundet ins Eingabefeld ein.
(Beispiel: sind die Lösungen $\alpha_1=33{,}75°$ und $\alpha_2=146{,}25°$ , dann gib zunächst $34$ ein und überprüfe die Lösung und anschließend $146$ )
1. $\sin\alpha=0{,}5$ (6 Lösungen)
  °
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus und Kosinus am Einheitskreis
  erste Lösung mit Taschenrechner bestimmen
  $\displaystyle \sin\alpha$ $=$ $\displaystyle 0{,}5$ $\displaystyle \sin^{-1}\square$
  $\displaystyle \alpha$ $=$ $\displaystyle 30°$
  weitere Lösung zwischen 0° und 360°
  Der gefundene Winkel liegt im I. Quadranten. Der nächste Winkel, der den gleichen Sinuswert hat, liegt im II. Quadranten:
  $sin(30°)=sin(180°-30°)=sin(150°)$
  $\alpha_2=30°$
  Lösungen zwischen 0° und -360°
  Die beiden Lösungen können mithilfe der Beziehung $sin(\alpha)=sin(k\cdot360°+\alpha)$ mit $k=-1$ in den Bereich [-360°;0] übertragen werden:
  $sin(30°)=sin(-1\cdot 360°+30°)=sin(-330°)$
  $sin(150°)=sin(-1\cdot 360°+150°)=sin(-210°)$
  also $\alpha_3=-330°$ und $\alpha_4=-210°$
  Lösungen zwischen 360° und 720°
  Die beiden Lösungen 30° und 150° können mithilfe der Beziehung $sin(\alpha)=sin(k\cdot360°+\alpha)$ mit $k=1$ in den Bereich [360°;720°] übertragen werden:
  $sin(30°)=sin(1\cdot360°+30°)=sin(390°)$
  $sin(150°)=sin(1\cdot360°+150°)=sin(510°)$
  also $\alpha_5=390°$ und $\alpha_6=510°$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme eine Lösung mit dem Taschenrechner.
  Weitere Lösungen bekommst du durch die Zusammenhänge am Einheitskreis und die Zusammenhänge für negative Winkel und Winkel >360°
2. $\cos\alpha=\frac{\sqrt{2}}{2}$ (6 Lösungen)
  °
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus und Kosinus am Einheitskreis
  erste Lösung mit Taschenrechner bestimmen
  $\displaystyle cos\alpha$ $=$ $\displaystyle \frac{\sqrt2} 2$ $\displaystyle cos^-1(\square)$
  $\displaystyle \alpha$ $=$ $\displaystyle 45°$
  weitere Lösung zwischen 0° und 360°
  Der gefundene Winkel liegt im I. Quadranten. Der nächste Winkel, der den gleichen Kosinuswert hat, liegt im IV. Quadranten:
  $cos(45°)=cos(360°-45°)=cos(315°)$
  also $\alpha_2=315°$
  Lösungen zwischen 0° und -360°
  Die beiden Lösungen können mithilfe der Beziehung $cos(\alpha)=cos(k\cdot360°+\alpha)$ mit $k=-1$ in den Bereich [-360°;0] übertragen werden:
  $cos(45°)=cos(-1\cdot 360°+45°)=cos(-315°)$
  $cos(315°)=cos(-1\cdot360°+315°)=cos(-45°)$
  also $\alpha_3=-310°$ und $\alpha_4=-45°$
  Lösungen zwischen 360° und -720°
  Die beiden Lösungen können mithilfe der Beziehung $cos(\alpha)=cos(k\cdot360°+\alpha)$ mit $k=1$ in den Bereich [360°;720°] übertragen werden:
  $cos(45°)=cos(1\cdot360°+45°)=cos(405°)$
  $cos(315°)=cos(1\cdot360°+315°)=cos(675°)$
  also $\alpha_5=405°$ und $\alpha_6=675°$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme eine Lösung mit dem Taschenrechner.
  Weitere Lösungen bekommst du durch die Zusammenhänge am Einheitskreis und die Zusammenhänge für negative Winkel und Winkel >360°
3. $\sin\left(\alpha\right)=-1$ (? Lösungen)
  °
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus und Kosinus am Einheitskreis
  Besonderer Sinus-Wert!
  $\sin\left(\alpha\right)=-1$ gilt nur einmal im Einheitskreis für Winkel zwischen 0° und 360°, nämlich für $\alpha_1=270°$
  Weitere Winkel
  Weitere Lösungen erhältst du, indem du in den Zusammenhang $\sin\left(\alpha\right)=\sin\left(k\cdot360°+\alpha\right)$ die Werte $k=1$ und $k=-1$ einsetzt:
  $\sin\left(270°\right)=\sin\left(-1\cdot360°+270°\right)=\sin\left(-90°\right)$
  $\sin\left(270°\right)=\sin\left(1\cdot360°+270°\right)=\sin\left(630°\right)$
  also $\alpha_2=-90°$ und $\alpha_3=630°$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme eine Lösung mit dem Taschenrechner.
  Weitere Lösungen bekommst du durch die Zusammenhänge am Einheitskreis und die Zusammenhänge für negative Winkel und Winkel >360°

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle \left(\cos(60°)\right)^2+\left(\sin(60°)\right)^2$	$=$	$\displaystyle 1^2$
	↓	Setze den Wert für den Kosinus ein.
$\displaystyle \left(\frac{1}{2}\right)^2+\left(\sin(60°)\right)^2$	$=$	$\displaystyle 1^2$
$\displaystyle \frac{1}{4}+\left(\sin(60°)\right)^2$	$=$	$\displaystyle 1$	$\displaystyle -\frac{1}{4}$
$\displaystyle \left(\sin(60°)\right)^2$	$=$	$\displaystyle \frac{3}{4}$	$\displaystyle \sqrt{ }$
$\displaystyle \sin(60°)$	$=$	$\displaystyle \pm\sqrt{\frac{3}{4}}$
	↓	Weil $\sin(60°)$ überhalb der $x$ -Achse angetragen wurde, kommt nur das positive Ergebnis in Frage.
$\displaystyle \sin(60°)$	$=$	$\displaystyle \sqrt{\frac{3}{4}}$

$\displaystyle \sin\alpha$	$=$	$\displaystyle 0{,}5$	$\displaystyle \sin^{-1}\square$
$\displaystyle \alpha$	$=$	$\displaystyle 30°$

$\displaystyle cos\alpha$	$=$	$\displaystyle \frac{\sqrt2} 2$	$\displaystyle cos^-1(\square)$
$\displaystyle \alpha$	$=$	$\displaystyle 45°$

Aufgaben zum Sinus und Kosinus am Einheitskreis

1. Winkel

2. Winkel

3. Winkel

4. Winkel

5. Winkel

Hast du eine Frage oder Feedback?

1.Winkel im Bogenmaß

2. Winkel im Bogenmaß

3. Winkel im Bogenmaß

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

1.Winkel

2.Winkel

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Vorüberlegungen

Analyse der Antwortmöglichkeiten

Hast du eine Frage oder Feedback?

Vorüberlegungen

Es ist nützlich, die Winkel, die größer sind als 90° auf einen spitzen Winkel im I. Quadranten zurückzuführen, da die Beziehungsgleichungen für einen Winkel 0°<α<90°0°<\alpha<90°0°<α<90°formuliert sind.

Analyse der Antwortmöglichkeiten

Verwende α′=50°\alpha'=50°α′=50°aus den Vorüberlegungen für die Beziehungen, denn sin(230°)=−sin(50°)sin(230°)=-sin(50°)sin(230°)=−sin(50°) und die Beziehungsgleichungen sind nur für spitze Winkel.

Hast du eine Frage oder Feedback?

Vorüberlegungen

Analyse der Antwortmöglichkeiten

Hast du eine Frage oder Feedback?

erste Lösung mit Taschenrechner bestimmen

weitere Lösung zwischen 0° und 360°

Lösungen zwischen 0° und -360°

Lösungen zwischen 360° und 720°

Hast du eine Frage oder Feedback?

erste Lösung mit Taschenrechner bestimmen

weitere Lösung zwischen 0° und 360°

Lösungen zwischen 0° und -360°

Lösungen zwischen 360° und -720°

Hast du eine Frage oder Feedback?

Besonderer Sinus-Wert!

Weitere Winkel

Hast du eine Frage oder Feedback?

Es ist nützlich, die Winkel, die größer sind als 90° auf einen spitzen Winkel im I. Quadranten zurückzuführen, da die Beziehungsgleichungen für einen Winkel $0°<\alpha<90°$ formuliert sind.

Verwende $\alpha'=50°$ aus den Vorüberlegungen für die Beziehungen, denn $sin(230°)=-sin(50°)$ und die Beziehungsgleichungen sind nur für spitze Winkel.