Berechne die fehlenden Seiten und Winkel des gleichschenkligen Dreiecks ABC mit . Beachte, dass wir allgemeine gleichschenklige Dreiecke betrachten, die nicht unbedingt rechtwinklig sind..
a=44,2cm
c=63,4cm
Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus, Cosinus und Tangens
geg: a=b= 44,2cm c=63,4cm
ges: h,
Zur Verdeutlichung eine Skizze zeichnen.
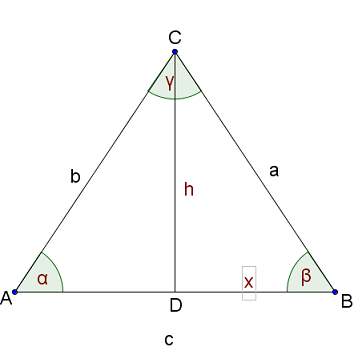
Zunächst berechnen.
berechnen, indem man in dem rechtwinkligen Dreieck den Satz des Pythagoras anwendet.
↓ Bekannte Werte einsetzen.
↓ Zunächst quadrieren.
↓ Nun subtrahieren.
↓ Wurzel ziehen.
mit Hilfe von Sinus berechnen.
↓ Werte einsetzen.
↓ Mit Hilfe des Taschenrechners berechnen.
↓ Es handelt sich hier um ein gleichschenkliges Dreieck mit
Da die Basiswinkel in einem gleichschenkligen Dreieck gleich sind, und alle Innenwinkel insgesamt ergeben, ausrechnen.
↓ Achtung: Das Dreieck ist kein rechtwinkliges Dreieck, da kein Winkel groß ist.
Hast du eine Frage oder Feedback?
a=114,5m
=32,3°
Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus, Cosinus und Tangens
Gegeben sind und
Gesucht sind , und
Zur Verdeutlichung machst du am besten eine Skizze.
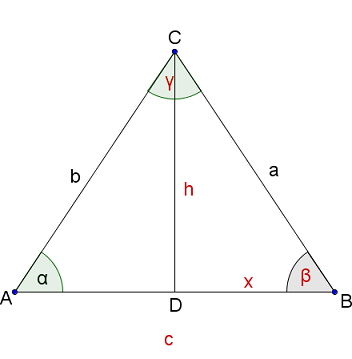
Da die Basiswinkel in einem gleichschenkligen Dreieck gleich sind, und alle Innenwinkel insgesamt ergeben, kannst du mit der Winkelsumme ausrechnen.
kannst du mit Hilfe des Sinus in dem rechtwinkligen Dreieck berechnen.
↓ Nach umstellen und Werte einsetzen.
↓ Weil die Höhe die Seite in der Mitte teilt, bekommt man gleich lange Strecken .
kannst du leicht berechnen, indem du die Seite verdoppelst.
kannst du berechnen, indem du in dem rechtwinkligen Dreieck den Satz des Pythagoras anwendest.
↓ Bekannte Werte einsetzen.
↓ Zunächst quadrieren.
↓ Nun subtrahieren.
↓ Wurzel ziehen.
Alternative: benutze den Kosinus im rechtwinkligen Dreieck
↓ Nach umstellen und Werte einsetzen.
↓ Damit hast du die Lösung
Anmerkung
Wenn du den Sinussatz kennst, kannst du auch direkt berechnen:
↓ Mit multiplizieren
↓ Werte einsetzen
Hast du eine Frage oder Feedback?
c=35,4cm
=43,9°
Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus, Cosinus und Tangens
geg: c=35,4cm =43,9°
ges: a, b, h, , x
Zur Verdeutlichung eine Skizze zeichnen.

Da die Basiswinkel in einem gleichschenkligen Dreieck gleich sind, und alle Innenwinkel insgesamt 180° ergeben, ausrechnen.
x berechnen, indem man die Seite c halbiert.
a mit Hilfe des Cosinus berechnen.
↓ Nach a umstellen und Werte einsetzen.
↓ h mit Hilfe des Tangens berechnen.
↓ Nach umstellen und Werte einsetzen.
↓ Hast du eine Frage oder Feedback?
h=14,8cm
28,3°
Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus, Cosinus und Tangens
Geg.: ;
Ges.:
Zeichne zur Verdeutlichung eine Skizze.
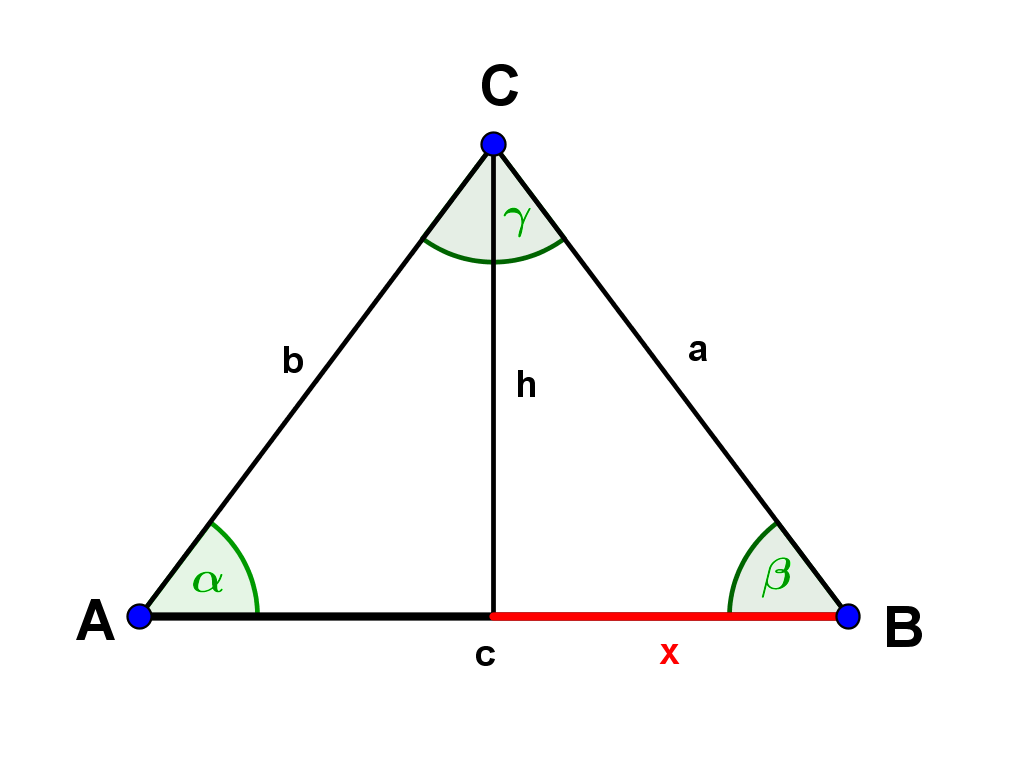
Da die Basiswinkel (hier: und ) in einem gleichschenkligen Dreieck gleich groß sind, und alle Innenwinkel insgesamt 180° ergeben (d.h. ), kannst mit dieser Information direkt ausrechnen.
mit Hilfe des Tangens berechnen.
↓ Nach x umstellen und Werte einsetzen.
↓ ↓ erhälst du, indem du die Seite verdoppelst (siehe Skizze).
mit Hilfe des Sinus berechnen.
↓ Nach umstellen und Werte einsetzen.
↓ Da es sich hier um ein gleichschenkliges Dreieck handelt, ist die Seitenlänge gerade gleich der Seitenlänge .
Hast du eine Frage oder Feedback?
a=146,4m
h=58,4m
Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus, Cosinus und Tangens
geg: ;
ges: , ,
Zur Verdeutlichung eine Skizze zeichnen.
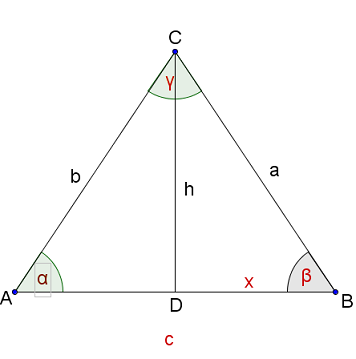
mit Hilfe des Sinus berechnen.
↓ Werte einsetzen und mit Hilfe des Taschenrechners berechnen.
Da die Basiswinkel in einem gleischenkligen Dreieck gleich sind, und alle Innenwinkel insgesamt ergeben, ausrechnen.
mit Hilfe des Tangens berechnen.
↓ Nach umstellen und Werte einsetzen.
↓ berechnen, indem man die Seite verdoppelt, dann die Höhe , in der Mitte teilt, sodass man gleich lange Strecken bekommt.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann → Was bedeutet das?
