▸ Wie stellt man die Formeln um?
Alternative Formulierung des Sinussatzes Durch Umformungen kann man den Sinussatz auch auf folgende Formen bringen:
sin ( α ) a = sin ( β ) b = sin ( γ ) c . a sin ( α ) = b sin ( β ) = c sin ( γ ) .
a b = sin ( α ) sin ( β ) a c = sin ( α ) sin ( γ ) b c = sin ( β ) sin ( γ ) b a = sin ( β ) sin ( α ) c a = sin ( γ ) sin ( α ) c b = sin ( γ ) sin ( β )
Man kann nach den einzelnen Größen auflösen:
a = b sin ( β ) ⋅ sin ( α ) = c sin ( γ ) ⋅ sin ( α ) a = sin ( β ) b ⋅ sin ( α ) = sin ( γ ) c ⋅ sin ( α )
b = a sin ( α ) ⋅ sin ( β ) = c sin ( γ ) ⋅ sin ( β ) b = sin ( α ) a ⋅ sin ( β ) = sin ( γ ) c ⋅ sin ( β )
c = a sin ( α ) ⋅ sin ( γ ) = b sin ( β ) ⋅ sin ( γ ) c = sin ( α ) a ⋅ sin ( γ ) = sin ( β ) b ⋅ sin ( γ )
Auflösung nach den Winkeln:
α = sin − 1 ( a b sin ( β ) ) = sin − 1 ( a c sin ( γ ) ) α = sin − 1 ( b a sin ( β ) ) = sin − 1 ( c a sin ( γ ) )
β = sin − 1 ( b a sin ( α ) ) = sin − 1 ( b c sin ( γ ) ) β = sin − 1 ( a b sin ( α ) ) = sin − 1 ( c b sin ( γ ) )
γ = sin − 1 ( c a sin ( α ) ) = sin − 1 ( c b sin ( β ) ) γ = sin − 1 ( a c sin ( α ) ) = sin − 1 ( b c sin ( β ) )
Wenn du aus einem Sinuswert in einem Dreieck den Winkel berechnen willst, beachte, dass die Gleichung sin ( α ) = x sin ( α ) = x 0 ∘ 0 ∘ 180 ∘ 18 0 ∘ zwei Lösungen hat:
mit dem α α sin − 1 ( x ) sin − 1 ( x ) 180 ∘ − α 18 0 ∘ − α
Der Satz des Pythagoras als Spezialfall des Kosinussatzes Für γ = 90 ∘ γ = 9 0 ∘ cos ( 90 ∘ ) = 0 cos ( 9 0 ∘ ) = 0 Satz des Pythagoras c 2 = a 2 + b 2 c 2 = a 2 + b 2
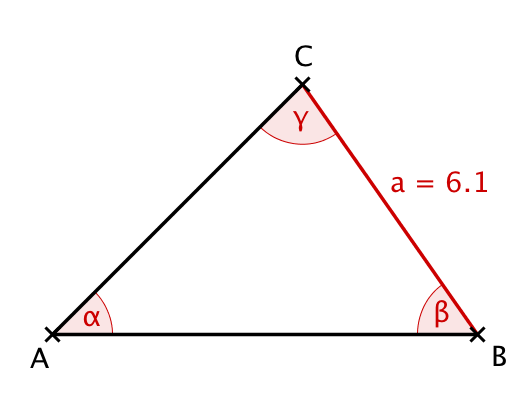
Beispiel Berechne zuerst mithilfe des Sinussatzes die Länge der Seite b b
a sin ( α ) = b sin ( β ) sin ( α ) a = sin ( β ) b
Setze die bekannten Werte ein.
6,1 sin ( 45 ∘ ) = b sin ( 55 ∘ ) sin ( 4 5 ∘ ) 6 , 1 = sin ( 5 5 ∘ ) b
⇒ b = 6,1 ⋅ sin ( 55 ∘ ) sin ( 45 ∘ ) = 7,1 ⇒ b = sin ( 4 5 ∘ ) 6 , 1 ⋅ sin ( 5 5 ∘ ) = 7 , 1
Berechne nun mithilfe des Kosinussatzes die Länge der Seite c c
c = a 2 + b 2 − 2 a b ⋅ cos ( γ ) c = a 2 + b 2 − 2 ab ⋅ cos ( γ ) = 6,1 2 + 7,1 2 − 2 ⋅ 6,1 ⋅ 7,1 ⋅ cos ( 80 ∘ ) = 8,5 = 6 , 1 2 + 7 , 1 2 − 2 ⋅ 6 , 1 ⋅ 7 , 1 ⋅ cos ( 8 0 ∘ ) = 8 , 5
Video Übungsaufgaben Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:Aufgaben zu Sinussatz und Kosinussatz