Die Parallelverschiebung ist eine Abbildung, die jeden Punkt entlang eines Verschiebungsvektor in dieselbe Richtung und um dieselbe Länge verschiebt.
Abbildungsgleichung der Parallelverschiebung
Anschaulich addiert man den Vektor , um den man verschieben möchte, zum Ortsvektor .
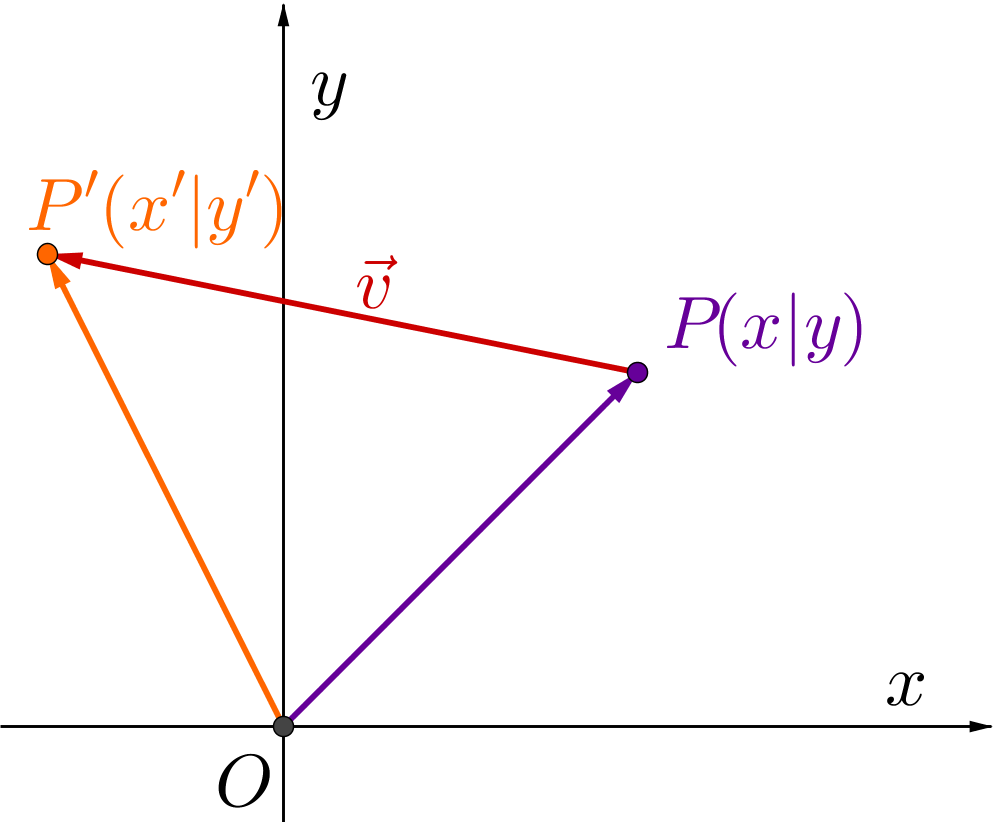
Somit ergibt sich .
Koordinatenform:
Matrixform:
Beispiel
Verschiebe den Punkt um den Vektor .
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
