Die Strahlensätze sind direkte Folgerungen aus der zentrischen Streckung.
Grundsätzlich lassen sich die Strahlensätze bei zwei Arten von Figuren anwenden, bei sogenannten "V−Figuren" und "X−Figuren".
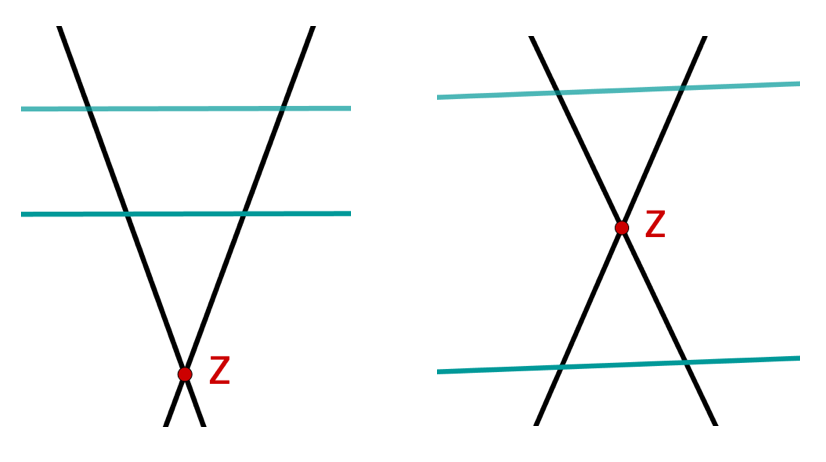
Die Strahlensätze
Voraussetzung
Um die Strahlensätze anzuwenden, müssen alle drei Voraussetzungen erfüllt sein:
richtig | falsch | |
|---|---|---|
Zwei Geraden und , die sich in einem Punkt schneiden. |  |  |
Diese beiden werden von zwei parallelen Geraden geschnitten. | 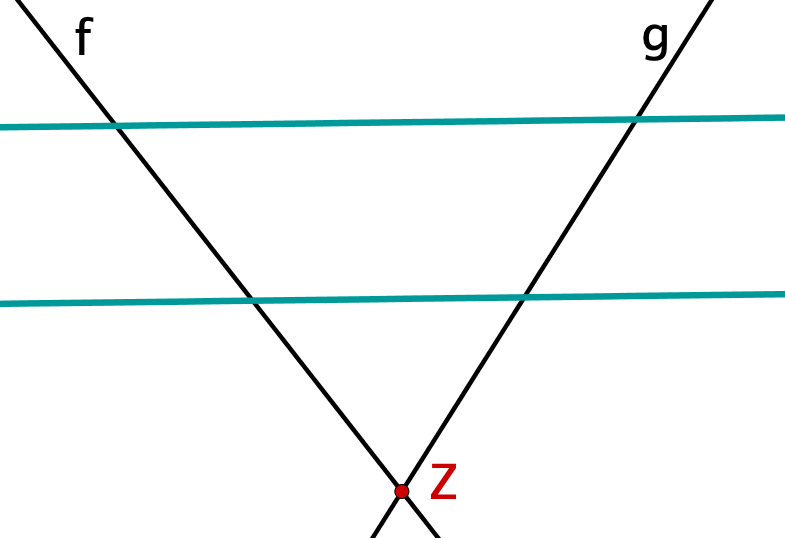 | 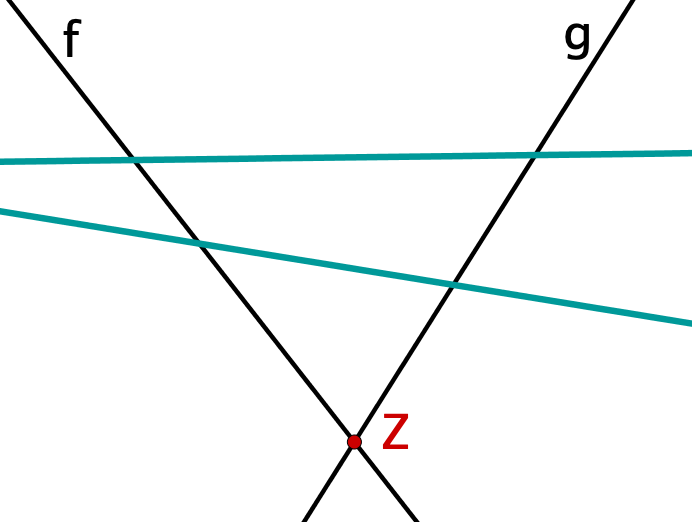 |
Wobei keine der beiden parallelen Geraden durch den Schnittpunkt der ersten beiden Geraden geht. | 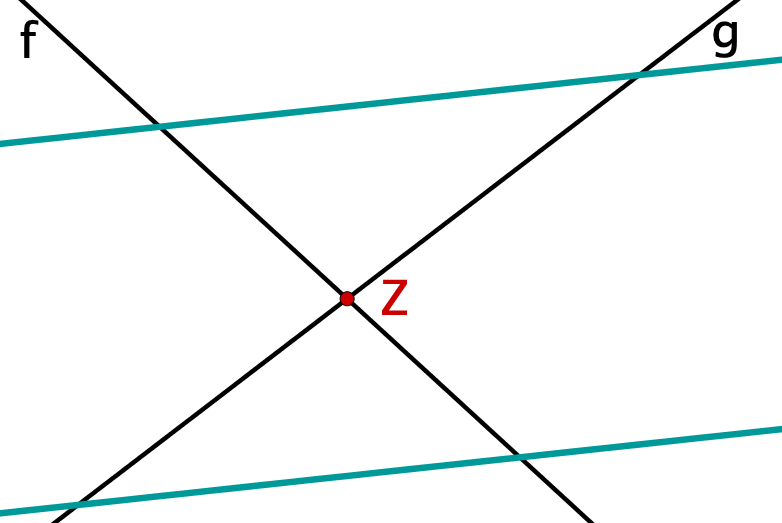 | 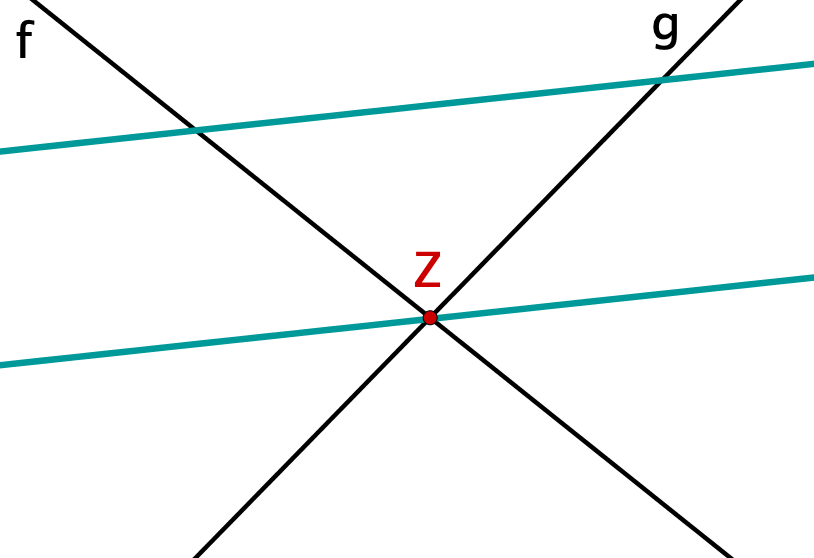 |
Aussage
Wenn die oben genannten Voraussetzungen erfüllt sind, dann gelten folgende Aussagen:
V-Figur
X-Figur

Umkehrung der Strahlensätze
Umkehrung des 1. Strahlensatzes: Gelten die oben beschriebenen Streckenverhältnisse des 1. Strahlensatzes, dann sind die beiden Geraden und parallel.
Die Umkehrung gilt im Allgemeinen nur für den 1. Strahlensatz und nicht für den 2. Strahlensatz der "V−Figuren" und "X−Figuren".
Wenn die oben beschriebenen Streckenverhältnisse des 2. Strahlensatzes gelten, dann müssen die beiden Geraden und nicht unbedingt parallel sein.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
