Dezimalzahlen sind Zahlen in Kommaschreibweise. Sie sind eine andere und in manchen Bereichen sehr gebräuchliche Art, Bruchzahlen anzugeben.
Man bezeichnet Dezimalzahlen daher oft auch als Dezimalbrüche.
ist ein Dezimalbruch und würde als Bruch oder lauten.
sind und ; wohl niemand würde dafür schreiben.
Ein dreiviertel Meter ist als Dezimalzahl geschrieben (d. h. )
Aufbau eine Dezimalzahl
Jede Dezimalzahl ist nach dem Muster Zahl - Dezimaltrennzeichen - Dezimalstellen aufgebaut.
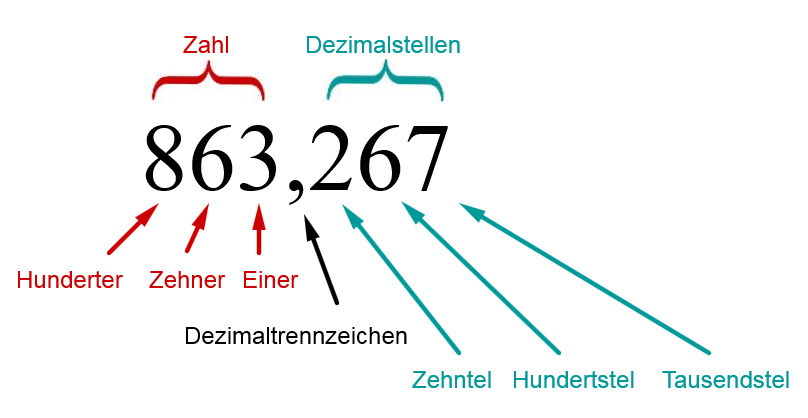
Das Dezimaltrennzeichen trennt die ganze Zahl von den Dezimalstellen. In Deutschland und Österreich wird dafür in der Regel ein Komma (,) verwendet, im englisch-sprachigen Raum und in der Schweiz ein Punkt (.).
Vor dem Dezimaltrennzeichen steht der ganzzahlige Anteil der Zahl. Manchmal macht man von Komma ausgehend nach jeweis drei Ziffern einen kleinen Zwischeraum (seltener einen Punkt), um die Lesbarkeit zu erhöhen
Hinter dem Dezimaltrennzeichen kommen die Dezimalstellen: Dabei bezeichnet
die erste Stelle nach dem Trennzeichen die Zehntel; die zweite Stelle nach dem Trennzeichen die Hundertstel; die dritte Stelle nach dem Trennzeichen die Tausendstel; die vierte Stelle nach dem Trennzeichen die Zehntausendstel usw. (Hunderttausendstel, Millionstel …)
Die in der Graphik dargestellte Dezimalzahl lautet in ausführlicher Bruchschreibweise also:
Dezimalzahlen in der Stellenwerttafel
Dezimalzahlen wie lassen sich problemlos in die Stellenwerttafel eintragen, wenn man diese entsprechend auf Zehntel (z), Hundertstel (h), Tausendstel (t), Zehntausendstel (zt) usw. erweitert.
... | H | Z | E | , | z | h | t | ... |
|---|---|---|---|---|---|---|---|---|
8 | 6 | 3 | , | 2 | 6 | 7 |
Anzahl der Dezimalstellen einer Dezimalzahl
Grundsätzlich kann eine Dezimalzahl beliebig viele Stellen hinter dem Komma haben. Drei Fälle sind zu unterscheiden:
1. Abbrechende Dezimalbrüche
In diesem Fall hören die Zahlen hinter dem Komma irgendwann auf (bwz. es folgen nur noch Nullen).
und ähnliches.
2. Periodische Dezimalbrüche
Diese Dezimalzahlen haben zwar unendlich viele Stellen hinter dem Komma, aber diese Stellen wiederholen sich ab einem bestimmten Punkt mit immer der gleichen Zahlenfolge.
Diese Zahlenfolge bezeichnet man als Periode der Dezimalzahl und kennzeichnet sie mit einem Querstrich über den betreffenden Ziffern.
(Anmerkung: Eine Dezimalzahl mit Periode "mittendrin", also zum Beispiel oder so ähnlich, macht dagegen keinen Sinn; denn wo sollte die stehen, wenn davor erst noch unendlich (!) viele Nullen abgewartet werden müssen? )
3. Nicht-abbrechende nicht-periodische Dezimalzahlen
Wenn man eine irrationale Zahl wie oder als Dezimalzahl zu schreiben versucht, erhält man eine Zahl mit unendlich vielen Stellen hinter dem Komma, die sich jedoch nicht periodisch wiederholen.
(Mehr dazu findest du hier: Wurzel 2)
(Mehr dazu kannst du hier nachlesen: Kreiszahl Pi)
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
