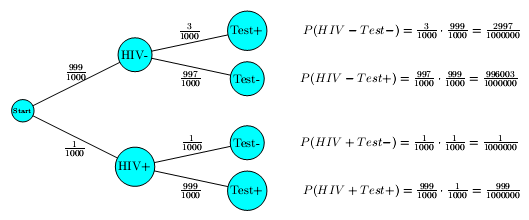
Im Jahr 200X waren in Deutschland ungefähr 0,1 % der Bevölkerung mit HIV infiziert. Mit Hilfe eines HIV-Tests kann festgestellt werden, ob eine Infektion vorliegt. Wenn ein Test eine Erkrankung anzeigt, nennt man das Ergebnis „positiv“, unabhängig davon, ob die Krankheit tatsächlich vorhanden ist oder nicht. Bei einer mit HIV infizierten Person beträgt die Wahrscheinlichkeit 99,9 %, dass der Test positiv ausfällt. Wenn eine Person nicht infiziert ist, dann beträgt die Wahrscheinlichkeit 99,7 %, dass der Test „negativ“ ausfällt.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass das Ergebnis eines HIV-Tests „positiv“ ausfällt.
Der Arzt teilt ein positives Testergebnis mit. Wie groß ist die Wahrscheinlichkeit dafür, dass die Person tatsächlich infiziert ist?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?