Gemischte Aufgaben zur Wahrscheinlichkeit

Wiederhole wichtige Grundlagen und vertiefe dein Wissen zur Wahrscheinlichkeit mit diesen gemischten Übungsaufgaben!

1
Zwei gleich gute Fußballvereine treten gegeneinander an. Sieg und Niederlage sind daher gleich wahrscheinlich. Ein Unentschieden führt zu einer Verlängerung, bei der eine Entscheidung höchstwahrscheinlich eintritt. Ein Unentschieden tritt nur in $\frac1{10}$ aller Spiele auf.
1. Wie heißt ein Ergebnisraum $\operatorname{\Omega}$ ?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ergebnisraum
  $\Omega=$ {Verein A gewinnt, Verein B gewinnt, Unentschieden}
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Wie groß ist die Wahrscheinlichkeit für ein Unentschieden?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
  P{"Unentschieden"} $=\frac1{10}=10\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Wie groß ist die Wahrscheinlichkeit dafür, dass Verein A gewinnt?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
  $\mathrm{P\{"Unentschieden"}\} =\frac1{10}=10\%$
  Bestimme das Gegenereignis.
  $\mathrm{P\left\{"kein\;Unentscheiden"\right\}}=\;1-\frac1{10}=\frac9{10}$
  Da beide Vereine die gleiche Wahrscheinlichkeit haben zu gewinnen, ergibt sich die Wahrscheinlichkeit, dass Verein A gewinnt, indem man die Wahrscheinlichkeit, dass kein Unentschieden auftritt durch 2 dividiert.
  $\mathrm{P\{"Verein \;A \;gewinnt"\}}=\frac9{10}:\;2=$
  $=\frac9{20}=0{,}45=45\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Wie groß ist die Wahrscheinlichkeit dafür, dass Verein A nicht verliert?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
  $P(\text{"Verein A verliert nicht")}=$
  $= P(\text{"Unentschieden")}+P(\text{"Verein A gewinnt")}=$
  $=\frac1{10}+\frac9{20}=$
  $=\frac2{20}+\frac9{20}=$
  $=\frac{11}{20}=0{,}55=55\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Malte hat drei Freunde, Andreas, Benjamin und Clemens. Andreas besucht Malte doppelt so oft wie Benjamin. Clemens dagegen besucht ihn nur halb so oft wie Benjamin. Es kommen nie zwei seiner Freunde gleichzeitig. Malte hört es an der Tür klingeln.
Mit welcher Wahrscheinlichkeit ist es
Andreas
Benjamin
Clemens
Andreas oder Benjamin?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichungen aufstellen
Stelle die Terme für die jeweiligen Besuche der Freunde auf.
Besuche Benjamin = x
Besuche Andreas = 2x
Besuche Clemens = 0,5x
Teilaufgabe 1:
Besuche Benjamin = x
Besuche Andreas = 2x
Besuche Clemens = 0,5x
Dividiere die Besuche von Andreas durch die Summe aller Terme um die Wahrscheinlichkeit zu berechnen.
$\dfrac{2x}{3{,}5x}=$
Kürze $x$ und schreibe als Prozentzahl.
$=\dfrac47\approx57\%$
Teilaufgabe 2:
Besuche Benjamin = x
Besuche Andreas = 2x
Besuche Clemens = 0,5x
Dividiere die Besuche von Benjamin durch die Summe aller Terme um die Wahrscheinlichkeit zu berechnen.
$\dfrac{1x}{3{,}5x}=$
Kürze $x$ und schreibe als Prozentzahl.
$=\dfrac27\approx29\%$
Teilaufgabe 3:
Besuche Benjamin = x
Besuche Andreas = 2x
Besuche Clemens = 0,5x
Dividiere die Besuche von Clemens durch die Summe aller Terme um die Wahrscheinlichkeit zu berechnen.
$=\dfrac{0{,}5x}{3{,}5x}=$
Kürze $x$ und schreibe als Prozentzahl.
$=\dfrac17\approx14\%$
Teilaufgabe 4:
Wahrscheinlichkeit Benjamin = $\frac27$
Wahrscheinlichkeit Andreas = $\frac47$
Addiere die Wahrscheinlichkeiten von Andreas und Benjamin und schreibe als Prozentzahl.
$\dfrac47+\dfrac27=\dfrac67\approx86\%$
3
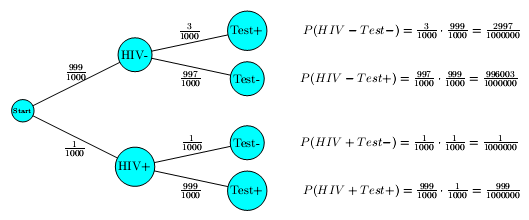
Im Jahr 200X waren in Deutschland ungefähr 0,1 % der Bevölkerung mit HIV infiziert. Mit Hilfe eines HIV-Tests kann festgestellt werden, ob eine Infektion vorliegt. Wenn ein Test eine Erkrankung anzeigt, nennt man das Ergebnis „positiv“, unabhängig davon, ob die Krankheit tatsächlich vorhanden ist oder nicht. Bei einer mit HIV infizierten Person beträgt die Wahrscheinlichkeit 99,9 %, dass der Test positiv ausfällt. Wenn eine Person nicht infiziert ist, dann beträgt die Wahrscheinlichkeit 99,7 %, dass der Test „negativ“ ausfällt.
1. Bestimmen Sie die Wahrscheinlichkeit dafür, dass das Ergebnis eines HIV-Tests „positiv“ ausfällt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm
  $\mathrm{P(HIV+,Test+) + P(HIV-,Test+)} =$
  Addiere die beiden Pfade, bei denen der Test positiv ausfällt.
  $=\frac{999}{1000000}+\frac{2997}{1000000}=\frac{3996}{1000000}$
  Rechne in Prozent um.
  $\Rightarrow\;\;$ Der Test fällt zu $0{,}3996\%$ Positiv aus.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Der Arzt teilt ein positives Testergebnis mit. Wie groß ist die Wahrscheinlichkeit dafür, dass die Person tatsächlich infiziert ist?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stochastik
  Wir wählen als Bedingung B = "Arzt teilt positives Testergebnis mit"
  Berechne die gesuchte bedingte Wahrscheinlichkeit.
  $P_B\left(HIV+,Test+\right)=$
  Verwende die Definition der bedingten Wahrscheinlichkeit.
  $=\frac{P\left(HIV+,Test+\right)}{P\left(HIV+,Test+\right)+P\left(HIV-,Test+\right)}=$
  Lese die Ergebnisse aus Aufgabe a) ab.
  $\frac{{\displaystyle\frac1{1000}}\cdot\displaystyle\frac{999}{1000}}{{\displaystyle\frac1{1000}}\cdot{\displaystyle\frac{999}{1000}}+{\displaystyle\frac{999}{1000}}\cdot\displaystyle\frac3{1000}}=$
  $=\frac14=25\%$
  $\Rightarrow\;\;$ Zu 25% ist die getestete Person tatsächlich infiziert.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

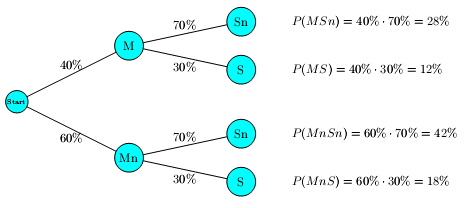
Die Beliebtheit einer neuen Fernsehsendung wird untersucht. Folgende Ergebnisse der Umfrage werden veröffentlicht: 25 % der Zuschauer sind jünger als 20 Jahre; von diesen haben 70 % eine positive Meinung zur Sendung. Von den restlichen Zuschauern haben immerhin 40 % eine positive Meinung.

Mit welcher Wahrscheinlichkeit ist ein zufällig ausgewählter Zuschauer jünger als 20 Jahre und hat eine positive Meinung zur Sendung?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeiten
Bezeichne die Ereignisse wie folgt:
$J$ =Jünger als 20 Jahre, $\overline J$ =Älter als 20 Jahre
$M$ =positive Meinung, $\overline M$ =negative Meinung
Verwende die Formel für die bedingte Wahrscheinlichkeit.
geg.:
$P_J\left(M\right)=70\%$
$P_{\overline{J}}\left(M\right)=40\%$
$\mathrm P(\mathrm J)=25\%$
ges.: $\;P\left(J\cap M\right)$
$\mathrm{P}_{\mathrm{J}}\left(\mathrm{M}\right)=\frac{\mathrm{P}\left(\mathrm{J}\cap\mathrm{M}\right)}{\mathrm{P}\left(\mathrm{J}\right)}$
$\Rightarrow P\left(J\cap M\right)={\mathrm P}_\mathrm J\left(\mathrm M\right)\cdot \mathrm P\left(\mathrm J\right) = 0{,}25\cdot0{,}7=17{,}5\%$
$\Rightarrow\;$ Ein zufällig ausgewählter Zuschauer ist mit einer Wahrscheinlichkeit von 17,5% jünger als 20 Jahre und hat eine positive Meinung zur Sendung.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Mit welcher Wahrscheinlichkeit hat ein zufällig ausgewählter Zuschauer keine positive Meinung zur Sendung?

5
Susi und Max werfen gleichzeitig je einen Stein auf eine 10 m entfernte Pfütze. Susis Treffsicherheit beträgt 30 %, die von Max 40%. Mit welcher Wahrscheinlichkeit trifft mindestens ein Stein sein Ziel?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Pfadregeln
$P("\mathrm{Max \;trifft \;nicht \;und \;Susi \;trifft"})=$
$=0{,}6\cdot0{,}3=0{,}18=18\%$
$\mathrm{P("Max \;trifft \;und \;Susi \;nicht")}=$
$=0{,}4\cdot0{,}7=0{,}28=28\%$
$\mathrm{P("Max \;trifft \;und \;Susi \;trifft")}=$
$=0{,}4\cdot0{,}3=0{,}12=12\%$
Wende die Pfadregeln an.
$P("\mathrm{Mindestens}\;\mathrm{einer}")=\underbrace{18\%}_{\mathrm{nur Susi}}+\underbrace{28\%}_{\mathrm{nur Max}}+\underbrace{12\%}_{\mathrm{beide}}=58\%$
Betrachte alternativ das Gegenereignis, dass keiner der beiden trifft und ziehe das Ergebnis von 1 ab.
Alternativ:
$P(\mathrm{"Mindestens\;einer"})=1-0{,}6\cdot0{,}7=58\%$
Baumdiagramm
6
Ein Affe sitzt vor einem Laptop, dessen Tastatur nur die 26 Buchstaben des lateinischen Alphabets enthält. Er schlägt wahllos 10 mal auf eine beliebige Taste. Mit welcher Wahrscheinlichkeit tippt er das Wort MATHEMATIK?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
Die Wahrscheinlichkeit für eine bestimmte Taste ist $\frac1{26}$ . Der Nenner ändert sich nicht, da das Experiment bei jedem Schlag neu beginnt. Dies wird 10-mal wiederholt.
$P(\mathrm{„MATHEMATIK“})=\left(\frac{1}{26}\right)^{10}$ $=7{,}083803739\cdot10^{-15}$
7
Es soll zufällig eine vierstellige Zahl aus den Ziffern 1, 2, 3 und 4 gebildet werden, bei der jede der Ziffern mehrmals vorkommen darf.
1. Beschreibe den Ablauf eines geeigneten Zufallsexperiments.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Als geeignetes Zufallsexperiment bietet sich das Drehen eines Glückrades mit 4 gleichgroßen Segmenten an. Dabei steht in jedem Segment eine Zahl zw. $1$ und $4$ und keine dieser Zahlen kommt doppelt vor.
  Wenn du das Glücksrad nun viermal drehst und dir jedes Mal die gedrehte Zahl aufschreibst, erhälst du eine vierstellige Zahl, die zufällig gebildet wurde, und jede Ziffer zw. $1$ und $4$ kann auch mehrmals vorkommen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Wie viele verschiedene Ergebnisse sind möglich?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kombinatorik
  Du kannst die Aufgabe mithilfe eines Baumdiagramms lösen. Du hast bei jeder Drehung jeweils 4 Möglichkeiten.Also gibt es
  $4^4=$ 256 Möglichkeiten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Ermittle die Wahrscheinlichkeiten folgender Ereignisse:
  A: Die Zahl enthält mindestens eine 2. B: Die gebildete Zahl endet auf 2.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Teilaufgabe 1
  Gesucht ist die Wahrscheinlichkeit, dass mindestens eine $2$ vorkommt.
  Verwende das Gegenereignis.
  $P("mind.eine \ 2")$ $=1-P("keine\;2")$
  Bestimme die Wahrscheinlichkeit des Gegenereignisses. Es gilt:
  Da keine $2$ vorkommen soll, gibt es nur noch $3$ Ziffern für die $4$ stellige Zahl. Wie in Teilaufgabe b) erhälst du z.B. mithilfe eines Baumdiagramms, dass $|A|=3^4$ ist.
  $|A|=|\{"keine 2"\}|=3^4$
  $|\Omega|=4^4$ (Teilaufgabe b) )
  $\Rightarrow P("keine\;2")=\left(\frac34\right)^4$
  $\Rightarrow P("mind.\;eine\;2")=1-\left(\frac34\right)^4=\frac{175}{256}\approx0{,}68=68\%$
  Teilaufgabe 2
  Gesucht ist die Wahrscheinlichkeit, dass die gebildete vierstellige Zahl am Ende eine 2 enthält.
  Es gilt:
  $P(A)=\frac{\left|A\right|}{\left|\Omega\right|}=\frac{|\{\text{"Zahl enthält eine 2 am Ende"}\}|}{|\Omega|}$
  Die Mächtigkeit von $\Omega$ wurde bereits in Teilaufgabe b) bestimmt. Bestimme die Mächtigkeit des Ereignisses $A$ , dass die vierstellige Zahl, eine $2$ am Ende enthält.
  Da der letzte Platz fix ist und die Ziffern mehrmals vorkommen können, können 4 Zahlen für 3 Plätze gewählt werden.
  $\Rightarrow |A|=4^3$
  Berechne nun $P(A)$ .
  $P(A)=\frac{\left|A\right|}{\left|\Omega\right|}=\frac{|\{\text{"Zahl enthält eine 2 am Ende"}\}|}{|\Omega|}=\frac{4^3}{4^4}=\frac14=0{,}25=25\%$
  Alternativ: Einfacher ist, zu erkennen, dass die $3$ vorderen Stellen für die Lösung irrelevant sind. Eine Ziffer von 4 an einer Stelle zu wählen, hat eben einfach eine Wahrscheinlichkeit von $25\%$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
8
Ein Würfel wird dreimal nacheinander geworfen. Mit welcher Wahrscheinlichkeit erscheint
1. keine Sechs ?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
  Wahrscheinlichkeit keine Sechs zu Würfeln liegt bei $\frac56$ $=$ $\frac{\mathrm{Anzahl}\;\mathrm{aller}\;\mathrm{günstigen}\;\mathrm{Ergebnisse}}{\mathrm{Anzahl}\;\mathrm{aller}\;\mathrm{möglichen}\;\mathrm{Ergebnisse}}$ . Da dreimal gewürfelt wird, muss diese Wahrscheinlichkeit dreimal multipliziert werden.
  $P=\frac{5}{6}\cdot\frac{5}{6}\cdot\frac{5}{6}\approx\;0{,}58\;=\;58\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. genau eine Sechs ?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
  Es ergibt sich Wahrscheinlichkeit $\frac16$ für die gewürfelte $6$ und $\frac56\cdot\frac56$ für die beiden Fehlversuche.
  Da die 6 in jedem der drei Würfe auftreten kann muss die Gesamtwahrscheinlichkeit noch mit $3$ multipliziert werden.
  $P=\frac16\cdot\frac56\cdot\frac56\cdot3\;\approx\;0{,}347\;=\;35\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. höchstens eine Sechs ?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
  "Höchstens eine Sechs" entspricht "entweder keine oder genau eine Sechs"
  $P=\underbrace{\frac56\cdot\frac56\cdot\frac56}_{a)}+\underbrace{\frac16\cdot\frac56\cdot\frac56\;\cdot3}_{b)}\;\approx\;0{,}926\;=\;93\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. mindestens eine Sechs ?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
  "Mindestens eine Sechs" entspricht "Alles außer keine Sechs.
  $P=1-\underbrace{\frac56\cdot\frac56\cdot\frac56}_{a)}\approx\;0{,}42\;=\;42\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
9
In einer Urne sind eine schwarze und drei weiße Kugeln; in einer anderen zwei schwarze und zwei weiße Kugeln. Ein Münzwurf entscheidet darüber, aus welcher der beiden Urnen eine Kugel gezogen werden muss. Ist die gezogene Kugel schwarz, so erhält man einen Gewinn.
1. Wie groß ist die Gewinnwahrscheinlichkeit?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stochastik
  Gewinnwahrscheinlichkeit Urne 1
  Inhalt: $1$ schwarze Kugel, $3$ weiße Kugeln; Schwarze ist Gewinn
  $\frac{1}{4}=$ Anteil der Schwarzen
  $\frac12=$ Wahrscheinlichkeit Urne 1 zu erhalten.
  Multipliziere die beiden Werte.
  $\mathrm{P(Gewinn\;Urne \;1)}=\frac14\cdot\frac12=\frac18$
  Gewinnwahrscheinlichkeit Urne 2
  Inhalt: $2$ schwarze Kugeln, $2$ weiße Kugeln; Schwarze ist Gewinn
  $\frac24=$ Anteil der Schwarzen
  $\frac12=$ Wahrscheinlichkeit Urne 2 zu werfen.
  Multipliziere die beiden Werte.
  $\mathrm{P(Gewinn\;Urne\;2)}=\frac24\cdot\frac12=\frac14$
  Gewinnwahrscheinlichkeit insgesamt
  Addiere die Gewinnwahrscheinlichkeiten von Urne 1 und Urne 2.
  $\mathrm{P(Gewinn\;insgesamt)}=\frac14+\frac18=$
  Bilde den Hauptnenner (hier $8$ ).
  $=\frac{2}{8}+\frac{1}{8}=\frac{3}{8}=37{,}5\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Nun erhält man die Erlaubnis, die $8$ Kugeln vor Spielbeginn so auf die zwei Urnen zu verteilen, dass in jeder $4$ Kugeln sind – für die Aufteilung der Farben gibt es dabei keinerlei Einschränkungen. Anschließend entscheidet wieder ein Münzwurf darüber, aus welcher Urne eine Kugel gezogen werden muss. Ist sie schwarz, so gewinnt man. Gibt es unter diesen Bedingungen eine optimale Verteilung der Kugeln auf die Urnen, sodass die Gewinnwahrscheinlichkeit möglichst groß wird? Begründe.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stochastick
  Insgesamt gibt es $3$ schwarze Kugeln und $5$ weiße. Sei $x$ die Anzahl schwarzer Kugeln in Urne $1$ und $y$ die Anzahl schwarzer Kugeln in Urne $2$ . Dann lässt sich die Gewinnwahrscheinlichkeit wie in Teilaufgabe $1$ berechnen:
  $\frac12\cdot\frac x4+\frac12\cdot\frac y4=\frac{x+y}8\underbrace=_{x+y=3}\frac38$
  Die Aufteilung auf die beiden Urnen spielt dabei keine Rolle.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Nun erhält man die Erlaubnis, die $8$ Kugeln vor Spielbeginn nach Belieben auf die zwei Urnen zu verteilen. Anschließend entscheidet wieder ein Münzwurf darüber, aus welcher Urne eine Kugel gezogen werden muss. Ist sie schwarz, so gewinnt man. Wie sieht die optimale Verteilung der Kugeln auf die Urnen aus?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stochastik
  Gegeben: $3$ schwarze Kugeln; $5$ weiße Kugeln
  Überlegung: Die Wahrscheinlichkeit ist am größten, wenn eine schwarze Kugel in der einen Urne (hier Urne 1) ist und alle restlichen Kugeln in der anderen Urne (hier Urne 2) sind.
  Gewinnwahrscheinlichkeit Urne 1
  Inhalt: $1$ schwarze Kugel
  $1=$ Anteil der Schwarzen.
  $\frac12=$ Wahrscheinlichkeit Urne 1 zu werfen.
  Multipliziere die beiden Werte.
  $\mathrm{P(Gewinn\;Urne \;1)}=1\cdot\frac12=\frac12$
  Gewinnwahrscheinlichkeit insgesamt
  Addiere die Gewinnwahrscheinlichkeiten von Urne 1 und Urne 2.
  $\mathrm{P(Gewinn\;insgesamt)}=\frac17+\frac12=$
  Bilde den Hauptnenner (hier $14$ ) und erweitere auf diesen.
  $=\frac{2}{14}+\frac{7}{14}=\frac{9}{14}\approx64{,}3\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
10
Ein „Teekenner“ behauptet, er könne die Teesorten First Flush (Begriff für Darjeeling- und Assam-Tees der ersten Pflückung nach dem Winter) und Second Flush (zweite Pflückung) am Geschmack unterscheiden. Er bekommt dazu einige Tassen vorgesetzt, wobei jede entweder First Flush oder Second Flush enthält. Äußerlich sind die verschiedenen Sorten nicht zu unterscheiden
1. Der „Teekenner“ bekommt zwei Tassen vorgesetzt. Mit welcher Wahrscheinlichkeit benennt er den Inhalt der beiden Tassen richtig, wenn er rät? Zeichne zunächst ein Baumdiagramm ( $R$ steht für "rät richtig", $Rn=\overline R$ steht für "rät falsch)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stochastik
  Zeichne ein Baumdiagramm.
  ⇒ Gesucht ist das Ereignis "RR" und dessen Wahrscheinlichkeit lässt sich ablesen: $\frac{1}{4}=25\%$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Der Test wird nun so abgeändert, dass der „Teekenner“ vier Tassen vorgesetzt bekommt. Er soll jeweils den Inhalt bestimmen. Erläutere, ob ihm deiner Meinung nach das Prädikat „Teekenner“ zu Recht zusteht, wenn er den Inhalt bei allen vier Tassen richtig zuordnet.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stochastik
  Die Wahrscheinlichkeit, dass er den Inhalt einer Tasse richtig errät, beträgt $\frac12$ . Dieses Experiment wird $4$ mal wiederholt, also ergibt sich die Gesamtwahrscheinlichkeit als:
  $\left(\frac{1}{2}\right)^4=0{,}0625=6{,}25\%$
  Es ergibt sich also eine äußerst geringe Gesamtwahrscheinlichkeit. Damit kann der Begriff "Kenner" infrage gestellt werden, da bei einer erneuten Durchführung des Tests er höchstwahrscheinlich nicht alle Tassen richtig zuordnen könnte.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Mit welcher Wahrscheinlichkeit tippt der „Teekenner“ mindestens bei einer der vier Tassen daneben, falls er eine Treffsicherheit von $70\ \%$ hat?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stochastik
  Bezeichne mit $A:$ "das Ereignis, dass er alle $4$ Tassen richtig zuordnet." Berechne die Wahrscheinlichkeit $P(A)$ :
  $P\left(A\right)=0.7^4$
  Die gesuchte Wahrscheinlichkeit ist die Wahrscheinlichkeit des Gegenereignisses $\overline{A}$ von $A$ , d.h. er kann nicht alle Tassen richtig zuordnen bzw. mindestens eine Tasse nicht.
  $\mathrm{P}(\overline{\mathrm{A}})=1-\mathrm{P}(\mathrm{A})$
  Setze den ausgerechneten Wert ein.
  $\mathrm{P}(\overline{\mathrm{A}})=1-0.7^4\approx 76\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Aus einem Skat Blatt ( $32$ Karten) werden an drei Spieler je zehn Karten ausgegeben.

Wie hoch ist die Wahrscheinlichkeit, dass ein Spieler die folgenden Karten hat:

Wir modellieren das Problem als Laplace-Experiment. Es gibt $\begin{pmatrix}32\\10\end{pmatrix}$ Möglichkeiten, $10$ aus $32$ Karten auszuwählen, d.h. $\left|\Omega\right|=\begin{pmatrix}32\\10\end{pmatrix}$ . Außerdem wissen wir, dass es $4$ Buben gibt und $28$ restliche Karten, die keine Buben sind.

$3$ bestimmte Buben, aber nicht den vierten?

genau drei Buben?

höchstens drei Buben?

Thomas geht aufs Oktoberfest. Er möchte sich dort am Schießstand einen Teddy schießen. Nüchtern hat er eine Treffsicherheit von $60\ \%$ , nach jeder Maß Bier sinkt seine Treffsicherheit um ein Drittel.

Mit welcher Wahrscheinlichkeit wird er mindestens einmal treffen,

wenn er dreimal schießt, und zwar einmal nüchtern, einmal nach der 1. und einmal nach der 2. Maß?
wenn er sechsmal schießt, und zwar einmal nüchtern, zweimal nach der 1. Maß und dreimal nach der 2. Maß?

Unteraufgabe 1

Wahrscheinlichkeit für Treffer:

Nüchtern: $0{,}6$

Nach 1 Maß: $0{,}6-\left(\frac13\cdot0{,}6\right)=0{,}4$

Nach 2 Maß: $0{,}4-\left(\frac13\cdot0{,}4\right)=\frac4{15}$

Da er mindestens einmal treffen muss, kann man die Wahrscheinlichkeit mit Hilfe des Gegenereignisses berechnen.

$\displaystyle \mathrm{P\left("mindestens\;1\;Treffer"\right)}$	$=$	$\displaystyle 1-\mathrm{P\left("kein\;Treffer"\right)}$
	$=$	$\displaystyle 1-\left[\left(1-0{,}6\right)\cdot \left(1-0{,}4\right)\cdot \left(1-\frac{4}{15}\right)\right]$
	$=$	$\displaystyle 1-\left[0{,}4\cdot 0{,}6\cdot \frac{11}{15}\right]$
	$≈$	$\displaystyle 0{,}824$
	$=$	$\displaystyle 82{,}4\ \%$

Unteraufgabe 2:

Wahrscheinlichkeit für Treffer:

Nüchtern: $0{,}6$

Nach 1 Maß: $0{,}6-\left(\frac13\cdot0{,}6\right)=0{,}4$

Nach 2 Maß: $0{,}4-\left(\frac13\cdot0{,}4\right)=\frac4{15}$

Da er mindestens einmal treffen muss, kann man die Wahrscheinlichkeit mithilfe des Gegenereignisses berechnen.

$\displaystyle \mathrm{P\left("mindestens\;1\;Treffer"\right)}$	$=$	$\displaystyle \mathrm{1-P\left("kein\;Treffer"\right)}$
	$=$	$\displaystyle 1-\left[\left(1-0{,}6\right)\cdot \left(1-0{,}4\right)\cdot \left(1-0{,}4\right)\cdot \left(1-\frac{4}{15}\right)\cdot \left(1-\frac{4}{15}\right)\cdot \left(1-\frac{4}{15}\right)\right]$
	$=$	$\displaystyle 1-\left[0{,}4\cdot 0{,}6\cdot 0{,}6\cdot \frac{11}{15}\cdot \frac{11}{15}\cdot \frac{11}{15}\right]$
	$≈$	$\displaystyle 0{,}943$
	$=$	$\displaystyle 94{,}3\ \%$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Wie oft muss er mindestens schießen, um mit mindestens $99\ \%$ iger Wahrscheinlichkeit mindestens einmal zu treffen,

wenn er noch nüchtern ist?
wenn er eine Maß getrunken hat?
wenn er zwei Maß getrunken hat?

Wir bestimmen die kleinste natürliche Zahl n, sodass Thomas nach n Schüssen mit mindestens $99\ \%$ iger Wahrscheinlichkeit trifft. Wie in Teilaufgabe a) verwenden wir dazu das Gegenereignis, d.h. wir berechnen diejenige kleinste natürliche Zahl n, sodass Thomas nach n Schüssen mit höchstens $1\ \%\ iger$ Wahrscheinlichkeit noch nicht getroffen hat.

Unteraufgabe 1

Thomas ist nüchtern, d.h.

$\mathrm{P\left("Thomas\;trifft"\right)=0{,}6}$

Stelle die Behauptung auf.

$\mathrm{P\left("Thomas\;hat\;nach\;n\;Schüssen\;mind.\;einmal\;getroffen"\right)\geq0{,}99}$

Formuliere das Ereignis um.

$\mathrm{\Leftrightarrow\;P\left("Thomas\;hat\;nach\;n\;Schüssen\;noch\;nicht\;getroffen"\right)\leq 0{,}01}$

Thomas schießt n-mal unabhängig hintereinander mit gleicher Wahrscheinlichkeit.

$\mathrm{\Leftrightarrow P\left("Thomas\;trifft\;nicht"\right)^n\leq0{,}01}$

Setze den Wert ein (Gegenereignis!).
	↓
$\displaystyle \left(1-0{,}6\right)^n$	$≤$	$\displaystyle 0{,}01$
$\displaystyle \left(0{,}4\right)^n$	$≤$	$\displaystyle 0{,}01$
	↓	Löse nach n auf.
$\displaystyle \ln \left(0{,}4\right)^n$	$≤$	$\displaystyle \ln \left(0{,}01\right)$
	↓	Wende die Rechenregeln für die ln-Funktion an.
$\displaystyle n\cdot \ln \left(0{,}4\right)$	$≤$	$\displaystyle \ln \left(0{,}01\right)$
	↓	Da $\ln\left(0{,}4\right)<0$ ändert sich das Ungleichheitszeichen.
$\displaystyle n$	$≥$	$\displaystyle \frac{\ln \left(0{,}01\right)}{\ln \left(0{,}4\right)}$
$\displaystyle n$	$≈$	$\displaystyle 5{,}03$

Wähle die kleinste natürliche Zahl, die größer als $5{,}03$ ist.

$\Rightarrow n=6$

Thomas muss also mindestens 6-mal schießen.

Unteraufgabe 2:

Thomas hat 1 Maß getrunken,

d.h. $\mathrm{P\left("Thomas\;trifft"\right)=0{,}4}$

Stelle die Behauptung auf.

$\mathrm{P\left("Thomas\;hat\;nach\;n\;Schüssen\;mind.\;einmal\;getroffen"\right)\geq0{,}99}$

Wir formulieren das Ereignis um.

$\mathrm{\Leftrightarrow\;P\left("Th.\;hat\;nach\;n\;Schüssen\;noch\;nicht\;getr."\right)\leq0{,}01}$

Thomas schießt n-mal unabhängig hintereinander mit gleicher Wahrscheinlichkeit.

$\mathrm{\Leftrightarrow P\left("Th.\;trifft\;nicht"\right)^n\leq0{,}01}$

Setze den Wert ein (Gegenereignis!).

$\displaystyle \left(1-0{,}4\right)^n$	$≤$	$\displaystyle 0{,}01$
	↓	Löse nach n auf.
$\displaystyle \left(0{,}6\right)^n$	$≤$	$\displaystyle 0{,}01$
$\displaystyle \ln \left(0{,}6\right)^n$	$≤$	$\displaystyle \ln \left(0{,}01\right)$
$\displaystyle n\cdot \ln \left(0{,}6\right)$	$≤$	$\displaystyle \ln \left(0{,}01\right)$
$\displaystyle n$	$≥$	$\displaystyle \frac{\ln \left(0{,}01\right)}{\ln \left(0{,}6\right)}$
$\displaystyle n$	$≈$	$\displaystyle 9{,}02$

Wähle die kleinste natürliche Zahl, die größer als $9{,}02$ ist.

$\Rightarrow n=10$

Thomas muss also mindestens 10-mal schießen.

Unteraufgabe 3

Thomas hat zwei Maß getrunken,

d.h. $\mathrm{P\left("Thomas\;trifft"\right)=\frac4{15}}$

$\mathrm{P\left("Thomas\;hat\;nach\;n\;Schüssen\;mind.\;einmal\;getroffen"\right)\geq0{,}99}$

Formuliere das Ereignis um.

$\mathrm{\Leftrightarrow\;P\left("Thomas\;hat\;nach\;n\;Schüssen\;noch\;nicht\;getroffen"\right)\leq0{,}01}$

Thomas schießt n-mal unabhängig hintereinander mit gleicher Wahrscheinlichkeit.

$\mathrm{\Leftrightarrow P\left("Thomas\;trifft\;nicht"\right)^n\leq0{,}01}$

Setze den Wert ein (Gegenereignis!).

$\displaystyle \left(1-\frac{4}{15}\right)^n$	$≤$	$\displaystyle 0{,}01$
$\displaystyle \left(\frac{11}{15}\right)^n$	$≤$	$\displaystyle 0{,}01$
	↓	Löse nach n auf.
$\displaystyle \ln \left(\frac{11}{15}\right)^n$	$≤$	$\displaystyle \ln \left(0{,}01\right)$
	↓	Wende die Rechenregeln für die ln-Funktion an.
$\displaystyle n\cdot \ln \left(\frac{11}{15}\right)$	$≤$	$\displaystyle \ln \left(0{,}01\right)$
	↓	Da $\ln\left(\frac{11}{15}\right)<0$ ändert sich das Ungleichheitszeichen.
$\displaystyle n$	$≥$	$\displaystyle \dfrac{\ln\left(0{,}01\right)}{\ln\left({\displaystyle\frac{11}{15}}\right)}$
$\displaystyle n$	$≈$	$\displaystyle 14{,}85$

Wähle die kleinste natürliche Zahl, die größer als $14{,}85$ ist.

$\Rightarrow n=15$

Thomas muss also mindestens 15-mal schießen.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

13
In den Spielregeln für ein Würfelspiel steht: „Man werfe beide Würfel und bilde aus den beiden oben liegenden Augenzahlen die größtmögliche Zahl.“ (Beispiel: Bei den Augenzahlen „1“ und „5“ ist das die Zahl „51“.)
1. Gib einen Ergebnisraum für dieses Spiel an und bestimme seine Mächtigkeit.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeitsrechnung
  Gib den Ergebnisraum an, indem du alle möglichen Ergebnisse auflistest.
  $\Omega=\left\{11;21;31;41;51;61;22;32;42;52;62;33;43;53;63;44;54;64;55;65;66\right\}$
  Gib die Mächtigkeit an, indem du die Anzahl aller Elemente in $\Omega$ ermittelst: $\left|\Omega\right|=21$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Gib folgende Ereignisse in Mengenschreibweise an und bestimme jeweils ihre Wahrscheinlichkeit:
  Die gebildete Zahl besteht aus zwei gleichen Ziffern.
  Die Zahl enthält mindestens eine 4.
  Die Einerziffer ist halb so groß wie die Zehnerziffer.
  Die Quersumme der Zahl ist 6.
  Die Zahl ist größer als 10.
  Die Zahl ist eine Primzahl.
  
  Unteraufgabe 1
  Der Ergebnisraum ist $M=\left\{11;22;33;44;55;66\right\}$ .
  Die Wahrscheinlichkeit beträgt mit Laplace: $\mathrm{P}=\frac{\left|\mathrm{M}\right|}{\left|\mathrm{\Omega}\right|}=\frac{6}{21}=\frac{2}{7}\approx29\ \%$
  Unteraufgabe 2
  $\mathrm N=\left\{41;42;43;44;54;64\right\}$
  $P=\frac{6}{21}=\frac{2}{7}\approx29\ \%$
  Unteraufgabe 3
  $M=\left\{21;42;63\right\}$
  $P=\frac{3}{21}=\frac{1}{7}\approx14\ \%$
  Unteraufgabe 4
  $M=\left\{51;42;33\right\}$
  $P=\frac{3}{21}=\frac{1}{7}\approx14\ \%$
  Unteraufgabe 5
  Da die kleinste Zahl im Ergebnissraum 11 ist, ist jede Zahl, insbesondere größer als 10. Somit ist der Ergebnisraum $\Omega$ und die Wahrscheinlichkeit 1:
  $M=\Omega$
  $P=100\ \%\$
  Unteraufgabe 6
  $M=\left\{11;31;41;43;53;61\right\}$
  $P=\frac{6}{21}=\frac{2}{7}\approx29\ \%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle P\left(\overline{M}\right)$	$=$	$\displaystyle P\left(J\cap\overline{M}\right)+P\left(\overline{J}\cap\overline{M}\right)$
$\displaystyle P\left(\overline{M}\right)$	$=$	$\displaystyle 0{,}075+0{,}45$
$\displaystyle P\left(\overline{M}\right)$	$=$	$\displaystyle 0{,}525$

$\displaystyle P\left(E\right)$	$=$	$\displaystyle \frac{\left\|E\right\|}{\left\|\Omega\right\|}$
	$=$	$\displaystyle \frac{\begin{pmatrix}3\\3\end{pmatrix}\cdot\begin{pmatrix}28\\7\end{pmatrix}}{\begin{pmatrix}32\\10\end{pmatrix}}$
	↓	Rechne den Binomialkoeffizienten aus, multipliziere und kürze.
	$=$	$\displaystyle \frac{1\cdot 1184040}{64512240}$
	$=$	$\displaystyle \frac{21}{3596}$
	$≈$	$\displaystyle 1{,}84\%$

$\displaystyle \mathrm{P\left("genau\;3\;Buben"\right)}$	$=$	$\displaystyle \frac{\begin{pmatrix}4\\3\end{pmatrix}\cdot\begin{pmatrix}28\\7\end{pmatrix}}{\begin{pmatrix}32\\10\end{pmatrix}}$
	↓	Rechne den Binomialkoeffizienten aus, multipliziere und kürze.
	$=$	$\displaystyle \frac{4\cdot1184040}{64512240}$
	$=$	$\displaystyle \frac{66}{899}$
	$≈$	$\displaystyle 7{,}34\%$

Der Einfachheit halber lösen wir diese Aufgabe mit Hilfe des Gegenereignisses.(Es gibt auch einen anderen Lösungsweg,der jedoch aufwändiger ist.)
	↓
$\displaystyle \mathrm{P\left("höchstens\;3\;Buben"\right)}$	$=$	$\displaystyle 1−P("4Buben")$
	$=$	$\displaystyle 1-\frac{\begin{pmatrix}4\\4\end{pmatrix}\cdot\begin{pmatrix}28\\6\end{pmatrix}}{\begin{pmatrix}32\\10\end{pmatrix}}$
	↓	Rechne den Binomialkoeffizienten aus, multipliziere und kürze.
	$=$	$\displaystyle 1-\frac{1\cdot376740}{64512240}$
	$=$	$\displaystyle 1-\frac{21}{3596}$
	$=$	$\displaystyle \frac{3575}{3596}$
	$≈$	$\displaystyle 99{,}41\%$

Gemischte Aufgaben zur Wahrscheinlichkeit

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Teilaufgabe 1:

Teilaufgabe 2:

Teilaufgabe 3:

Teilaufgabe 4:

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Baumdiagramm

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Teilaufgabe 1

Teilaufgabe 2

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Gewinnwahrscheinlichkeit Urne 1

Gewinnwahrscheinlichkeit Urne 2

Gewinnwahrscheinlichkeit insgesamt

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Gewinnwahrscheinlichkeit Urne 1

Gewinnwahrscheinlichkeit insgesamt

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Unteraufgabe 1

Unteraufgabe 2:

Hast du eine Frage oder Feedback?

Unteraufgabe 1

Unteraufgabe 2:

Unteraufgabe 3

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Unteraufgabe 1

Unteraufgabe 2

Unteraufgabe 3

Unteraufgabe 4

Unteraufgabe 5

Unteraufgabe 6

Hast du eine Frage oder Feedback?