Die Normalverteilung oder Gauß-Verteilung ist eine der wichtigsten Verteilungen in der Stochastik und Statistik.
Definition
Dichtefunktion
Hat eine Zufallsgröße den Erwartungswert , Varianz und die Wahrscheinlichkeitsdichte
,
so heißt sie normalverteilt, mit den Parametern und , kurz auch -verteilt. Man schreibt .
Für und heißt die Zufallsgröße standardnormalverteilt.
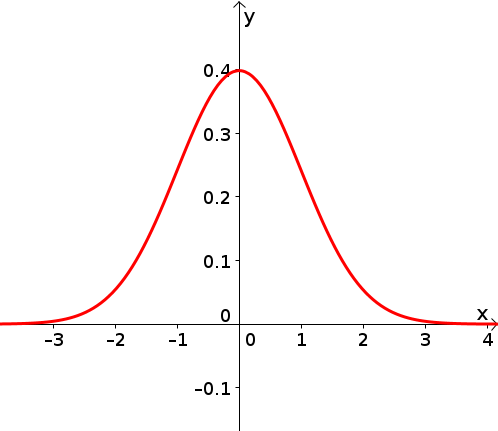
Im Graphen rechts ist die Funktion der Standardnormalverteilung abgebildet. Er heißt allgemein Gaußsche Glockenfunktion.
Verteilungsfunktion
Die Verteilungsfunktion einer Normalverteilung ist gegeben durch
Substituiere .
.
ist die Verteilungsfunktion der Standardnormalverteilung.
Die Werte der Standardnormalverteilung lassen sich im Tafelwerk der Stochastik nachlesen.
Eigenschaften
hat Erwartungswert .
hat Standardabweichung .
ist symmetrisch zur Symmetrieachse .
ist nie 0.
Für :
Annäherung der Binomialverteilung durch die Normalverteilung
Für große kann die Binomialverteilung durch die (Standard-)Normalverteilung angenähert (approximiert) werden. Ist so gilt:
und
Wie bei jeder Binomialverteilung ist
der Erwartungswert
die Standardabweichung
Nur bei großen Zahlen ist der Fehler durch die Näherung klein.
Achte darauf und richtig in die Formel einzusetzen.
Anwendung
Zufallsgrößen, bei denen die meisten Werte innerhalb eines gewissen Bereichs liegen und wenige Ausreißer nach oben und unten haben, sind meistens annähernd normalverteilt. Wie zum Beispiel bei
der Größe von Menschen
dem Gewicht von Kaffeepackungen
Messfehlern von Experimenten
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Normalverteilung
