Zu den Rechengesetzen für die Addition gehören das Kommutativgesetz (Vertauschungsgesetz) und das Assiozativgesetz (Klammergesetz).
Kommutativgesetz (Vertauschungsgesetz)
Nach dem Kommutativgesetz ist es egal, in welche Reihenfolge die Summanden haben, das Ergebnis ist immer dasselbe.
Beispiel
Peter hat zwei Murmeln und Kira drei. Zusammen haben sie dann fünf.
Aber auch wenn Peter drei Murmeln hat und Kira zwei, haben sie zusammen fünf Murmeln. Es ist egal in welcher Reihenfolge die Zahlen und addiert werden, das Ergebnis ist in beiden Fällen mit dasselbe.

Assoziativgesetz (Klammergesetz)
Wenn mehr als zwei Summanden addiert werden, helfen uns Klammern, zu wissen, welche Teile zuerst zusammengerechnet werden.
So werden bei der Addition
zuerst die eins und die zwei addiert, und zu deren Summe wird schließlich die drei addiert. Man erhält also
Bei der Addition
werden zuerst die zwei und die drei addiert, und zu deren Summe wird schließlich die eins addiert. Hier haben wir
Das Assoziativgesetz sagt uns, dass die Summe unverändert bleibt, egal wie die Klammern platziert werden.
Beispiel
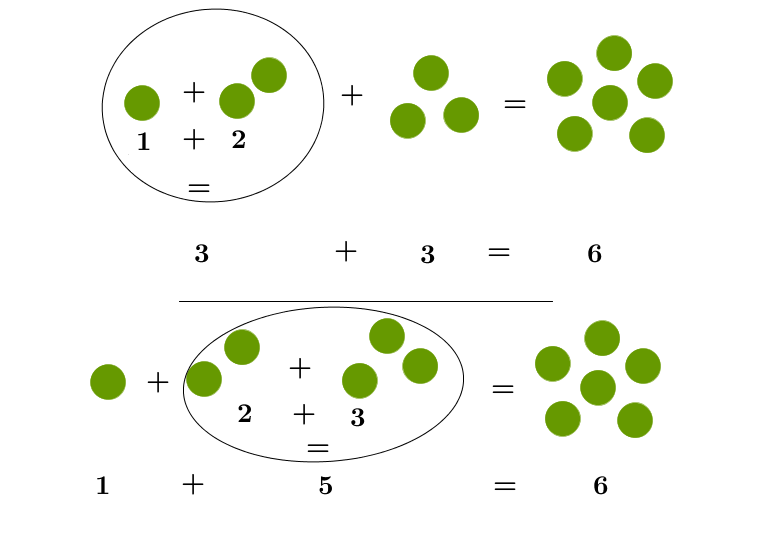
Peter hat eine Murmel, Kira zwei und Michi hat drei. Zuerst tun Peter und Kira ihre Murmeln zusammen - das sind drei. Dann bringt Michi seine dazu. Insgesamt haben sie 6 Murmeln.
Kira und ihr Michi können auch zuerst ihre Murmeln zusammen tun – das sind fünf Murmel. Später sammeln sie auch Peters Murmel mit ein. Auch hier haben sie zu Dritt insgesamt sechs Murmeln.
Diese Rechenregeln können wir verwenden, um möglichst vorteilhaft zu addieren. Wie das geht, kannst du im Artikel zu den Rechentricks nachlesen.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
