Wenn eine Dezimalzahl sehr viele Nachkommastellen hat und dadurch unhandlich wird, verwendet man oft anstelle der genauen Zahl einen gerundeten Wert.
Beispiel: , wenn man die Zahl auf zwei Stellen hinter dem Komma runden möchte.

(Das Zeichen "" bedeutet: "ist ungefähr gleich")
Grundprinzip
Beim Runden wird die ursprüngliche "lange" Dezimalzahl mit den vielen Nachkommastellen ersetzt durch eine "kürzere" Zahl mit weniger Nachkommastellen, die zwar nicht genau, aber ungefähr den gleichen Wert hat wie die wirkliche Zahl. Anders als beim bloßen "Abschneiden" der Dezimalzahl achtet man beim Runden aber darauf, dass die gerundete Zahl so nah wie möglich an der Ausgangszahl liegt.
Beispiel:
ergibt auf eine Stelle hinter dem Komma gerundet und nicht ; denn 1,79 liegt näher an 1,8 als an 1,7.
Technische Vorgehensweise
Schritt 1
Zuerst muss man wissen, auf welche Stelle gerundet werden soll, und wie viele Stellen hinter dem Komma die gerundete Zahl somit noch haben darf.
auf ganze Zahlen runden heißt: Die gerundete Zahl hat überhaupt keine Nachkommastellen mehr
auf Zehntel runden heißt: Die gerundete Zahl hat 1 Nachkommastelle.
auf Hundertstel runden heißt: Die gerundete Zahl hat 2 Nachkommastellen.
auf Tausendstel runden heißt: Die gerundete Zahl hat 3 Nachkommastellen.
usw.
Schritt 2
Die zu rundende Zahl unterteilt man nun in Gedanken in zwei Teile:
Der erste Teil geht bis zu der Stelle, auf die gerundet wird,
der zweite Teil ist der "Rest" der Zahl.
Beispiel:
Wenn man die Zahl auf Hundertstel runden möchte, unterteilt man die Zahl nach der zweiten Nachkommastelle, das heißt, zwischen der 5 und der 8:
Schritt 3
Jetzt schaut man sich die erste Zahl vom zweiten Teil der Zahl an, d. h. diejenige Stelle, die unmittelbar auf die Stelle, auf die gerundet werden soll, folgt.
Wenn diese Stelle eine oder ist, wird abgerundet, das heißt, man verwendet als gerundeten Wert einfach den ersten Teil der Zahl.
Beispiel:
ergibt auf Tausendstel gerundet den Wert , denn nach der 3. Stelle hinter dem Komma folgt eine 1.
Wenn diese Stelle eine oder ist, wird aufgerundet, das heißt, die letzte Stelle des ersten Teils der Zahl wird um 1 erhöht - sofern das noch geht und sie nicht bereits eine 9 war. Wenn sie bereits eine 9 war, müssen die letzte und die vorletzte (und eventuell sogar noch weitere Stellen) angepasst werden.
Beispiele:
ergibt auf Zehntel gerundet
ergibt auf die 4. Stelle hinter dem Komma gerundet ; denn da die 9 nicht auf 10 erhöht werden kann, muss die 19 auf 20 erhöht werden.
ergibt auf Tausendstel gerundet . Hier beeinflusst das Runden mehrere Stellen.
ergibt auf Hundertstel gerundet .
Auf ganze Zahlen runden
Auf ganze Zahlen runden heißt, dass man die ganze Zahl sucht, die der gegebenen Dezimalzahl am nächsten ist. Bei ganzen Zahlen ist das die Zahl selbst.
Abrunden bedeutet, dass bei Zehntelstellen von 0 bis einschließlich 4 auf die Zahl vor dem Komma gerundet wird.
Aufrunden bedeutet, dass bei Zehntelstellen von 5 bis einschließlich 9 auf die nächst größere Zahl gerundet wird.
Achtung! Es wird nicht auf kleinere Zahlen gerundet!
Beispiele an der Stellenwerttafel
E | z | h | |
|---|---|---|---|
Dezimalzahl | 0, | 7 | 3 |
Dezimalzah | 1, | 2 | 6 |
gerundete Zahl | 1, | 0 | 0 |
Bei 0,77 wird wegen der 7 an der Zehntelstelle auf die 1 gerundet
Bei 1,26 wird wegen der 2 an der Zehntelstelle auf die 1 abgerundet.
E | z | h | |
|---|---|---|---|
Dezimalzahl | 1, | 5 | 0 |
gerundete Zahl | 2, | 0 | 0 |
Bei der 1,5 wird wegen der 5 an der Zehntelstelle auf 2 gerundet.
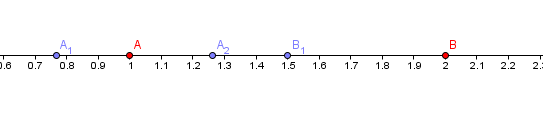
Beispiele am Zahlenstrahl
und werden auf gerundet, auf .
Rechenbeispiele
2,3 2
Weil die Zehntelstelle 3 zwischen 0 und 4 liegt, wird abgerundet, d.h. die 2 wird stehen gelassen.
3,7 4
Weil die Zehntelstelle 7 zwischen 5 und 9 liegt, wird aufgerundet, d.h. die 3 wird zur 4.
2,48 2
Weil die Zehntelstelle 4 zwischen 0 und 4 liegt, wird abgerundet, d.h. die 2 wird stehen gelassen.
Achtung Fehlerteufel Man darf bei mehreren Nachkommastellen nicht schrittweise runden! Folgende Rundung ist also falsch: 2,48 2,5 3
Sinnvoll runden
Häufig steht in Aufgabenstellungen die Forderung "Runde sinnvoll!" - Was ist damit gemeint? In verschiedenen Situationen, z.B. beim Rechnen mit Maßeinheiten, sind nur bestimmte Rundungen hilfreich. Bei Geldbeträgen ist es üblich, auf Hundertstel zu runden. Schließlich gibt es keine Tausendstel Euro.
Bei Maßeinheiten sind häufig mehrere Rundungen sinnvoll, je nachdem welche Angaben in der jeweiligen Situation gebraucht werden. Häufig reicht es, auf insgesamt 2 bis 3 Stellen zu runden. Für genaue Messergebnisse können auch 4 oder sogar 5 Stellen sinnvoll sein. Bei groben Abschätzungen reicht manchmal schon eine Stelle.
Beispielaufgabe:
Peter fährt 20 Minuten mit dem Auto. Er fährt beständig 100 km/h. Wie weit ist Peter gefahren? Runde das Ergebnis sinnvoll.
Lösung:
20 Minuten sind Stunde. In einer Stunde legt er 100 Kilometer zurück, also in Stunde Kilometer. Diese Zahl hat unendlich viele Stellen: Wir haben 33 km plus 333 m plus 33 cm plus 3 mm usw. Üblich ist es hier, auf ganze Kilometer zu runden, so wie bei Entfernungsangaben auf Verkehrsschildern.
Peter ist 33 Kilometer gefahren.
Aber auch die Entfernungsangabe „33,3 Kilometer“ wäre hier sinnvoll. Für sehr genaue Angaben, wären sogar „33,33 Kilometer“ oder „33,333 Kilometer“ in Ordnung. Und auch „ca. 30 Kilometer“ kann eine sinnvolle Antwort sein, vorausgesetzt, du möchtest eine ungefähre Distanz angeben.
Definitiv nicht sinnvoll ist z. B. eine Angabe auf den Millimeter genau, also „33,333333 Kilometer“ (das wären 8 Stellen). So genau lässt sich die Fahrstrecke nicht messen und üblicherweise ist es nicht wichtig, ob ein Auto einige Millimeter mehr oder weniger gefahren ist.
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Runden von Dezimalzahlen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
