Dieser Artikel befasst sich mit der Grundrechenart Addition.
Die Addition, umgangssprachlich auch Plus-Rechnen genannt, ist eine der vier Grundrechenarten. Oft sagt man statt „addieren“ auch „zusammenzählen“.
Die Zahlen, die addiert werden, nennt man Summanden, den Ausdruck 1. Summand + 2. Summand nennt man Summe und das Ergebnis der Rechnung Wert der Summe.
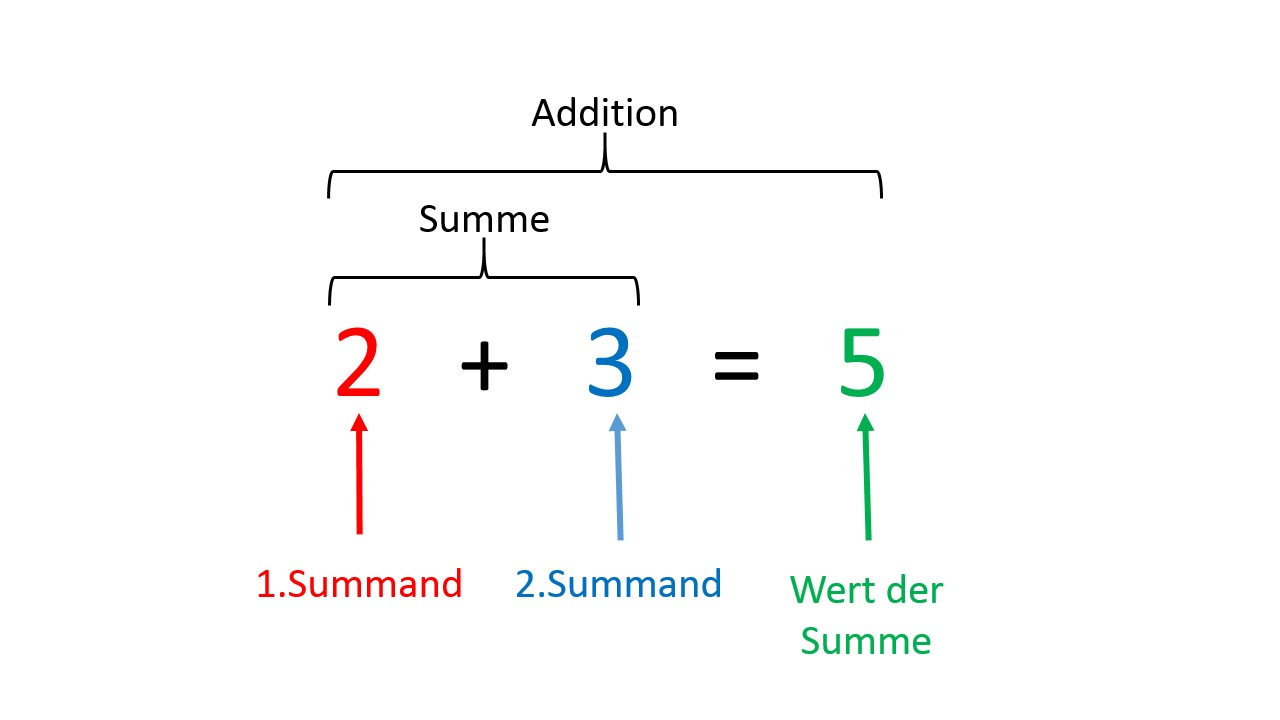
Wie kann man sich das vorstellen?
Mit Gegenständen
Wenn Peter zwei Murmeln hat und Kira drei, dann haben sie zusammen fünf Murmeln.
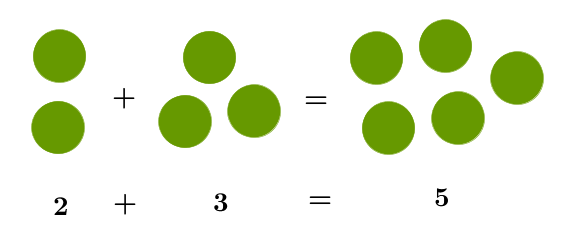
Mit einer Zahlengeraden
Mit der Zahlengerade können wir uns die Addition als Schrittezählen vorstellen.
Um 2 + 3 zu berechnen, markiert man zuerst die Zahl 2 auf der Zahlengerade und geht von dort aus drei „Schritte“ nach rechts. Die Zahl, auf der man landet, ist dann die Summe.

Schritte zählen ist nicht besonders schwer. Es kann aber viel Zeit kosten, vor allem wenn man große Zahlen addiert. Um große Zahlen zu addieren, kann man die schriftliche Additon verwenden.
Die besondere Zahl - Null
Wenn die Zahl Null ein Summand einer Summe ist, trägt sie zum Wert der Summe nichts bei, man kann sie beim Addieren also auch einfach weglassen. So gilt zum Beispiel
sowie
Die Null ist die einzige Zahl mit dieser Eigenschaft.
Übungsaufgaben
Laden
Laden
Laden
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
