Die zwei nach dem Physiker Kirchhoff benannten Regeln geben eine Grundlage zur Berechnung der Stromspannungen , Stromstärken und Widerständen innerhalb von Stromkreisen.
1. Kirchhoffsche Regel (Knotenregel)
Liegt eine Verzweigung in einem Stromkreis vor, so ist die Summe der Zweigströme vom Knotenpunkt weg gleich der Summe der verzweigten Ströme zum Knotenpunkt hin.
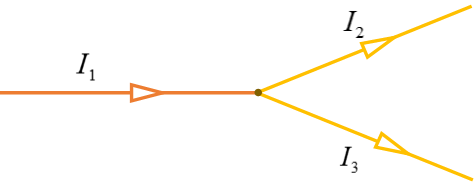
Das einfachste Beispiel ist eine Kreuzung, in der sich eine Leitung zum Knotenpunkt hin in zwei Leitungen weg vom Knoten auftrennt.
Hier fließt der Strom zum Knotenpunkt und wird in die zwei Zweige aufgeteilt. Dabei gilt:
Im Falle von mehreren Zweigen zum Knotenpunkt hin gilt dann:
Die Spannung bleibt jedoch in allen Zweigen gleich.
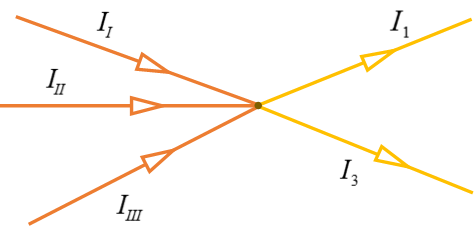
Zum Knotenpunkt hinfließt eine bestimmte Menge von Ladung. Die gleiche Menge an Ladung muss auch vom Knotenpunkt weg fließen, da keine Ladungen neu erzeugt werden und keine verloren gehen. Die Ladung bleibt erhalten.
Laden
Die 1. Kirchhoff'sche Regel ist sehr hilfreich bei der Berechnung in Parallelschaltungen.
2. Kirchhoffsche Regel (Maschenregel)
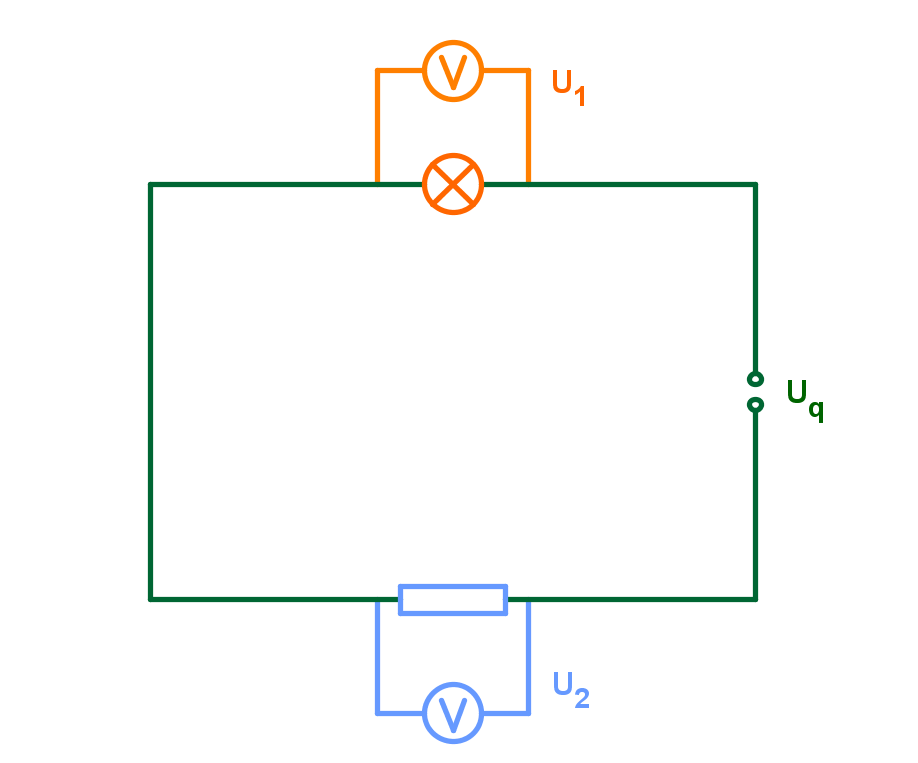
In eine Masche ist die Summe der Teilspannungen gleich der Spannungsquelle.
In dem rechten Stromkreis zum Beispiel ist die Spannung von der Quelle gleich der Summe der Teilspannungen an den Verbrauchern.
Für den Strom gilt
da hier, im Gegensatz zum 1. Kirchhoff'schen Regel, keine Verzweigung vorliegt.
Die 2. Kirchhoff'sche Regel ist sehr hilfreich bei der Berechnung in Reihenschaltungen.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
