Bestimme den Öffnungsfaktor und den Funktionsterm der folgenden Parabeln!
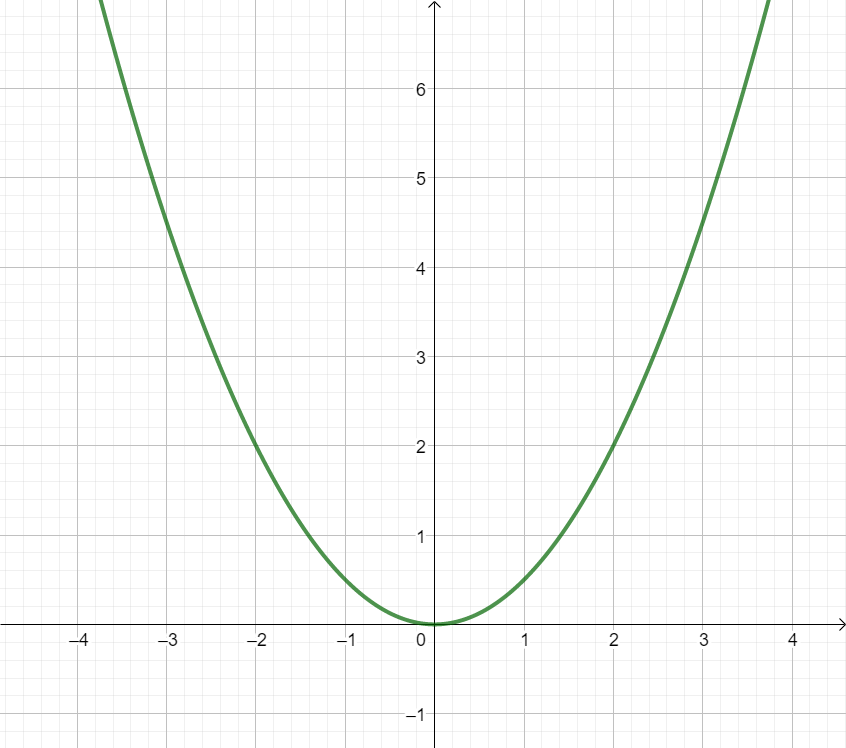
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm aufstellen für Parabeln
Hier berechnen wir den Funktionsterm, indem wir den Öffnungsfaktor bestimmen und mithilfe eines weiteren Punktes den Funktionsterm ausrechnen.
Suche dir nun einen Punkt, den du gut vom Funktionsgraphen ablesen kannst und der nicht der Scheitelpunkt ist.
Es bietet sich der Punkt an, weil da die Parabel genau eine Kästchen-Ecke trifft.
Setze die Koordinaten des Punktes in die allgemeine Form für die Parabel mit dem Scheitelpunkt ein.
Löse diese Gleichung nach auf!
Der Öffnungsfaktor hat also den Wert .
Aufstellen der Funktionsgleichung
Setze nun den Wert für den Öffnungsfaktor in die allgemeine Funktionsgleichung ein.
Die Funktionsgleichung der Parabel lautet .
Hast du eine Frage oder Feedback?
Hier gibt es verschiedene Lösungsansatze: Du kannst z.B: 3 Punkte ablesen und daraus die Funktion bestimmen oder den Öffnungsfaktor der Parabel bestimmen und dann mit einem weiteren Punkt die Funktion ausrechnen.
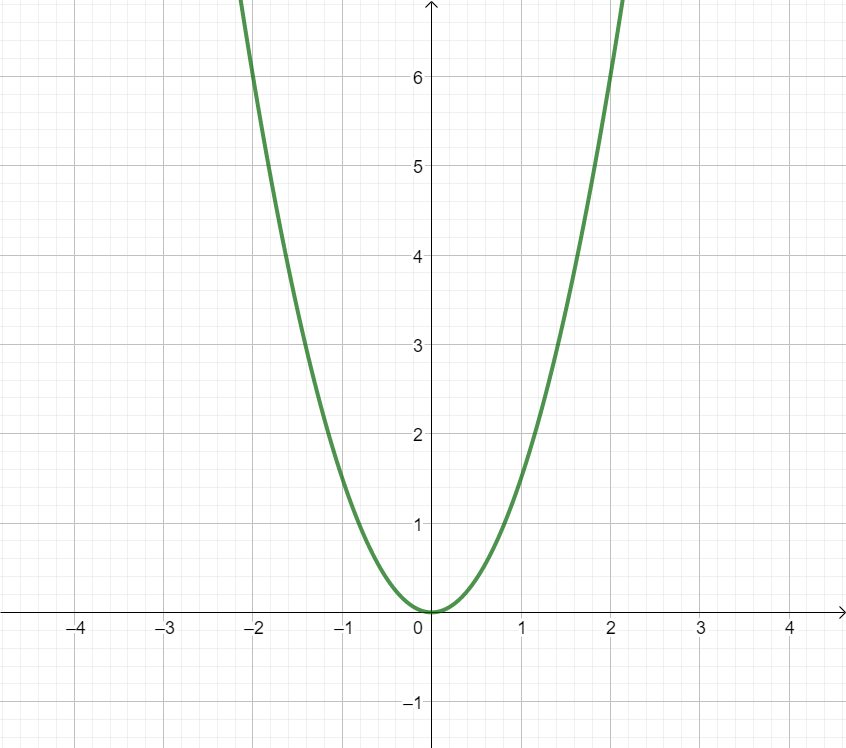
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm aufstellen für Parabeln
Hier berechnen wir den Funktionsterm, indem wir den Öffnungsfaktor bestimmen und mithilfe eines weiteren Punktes den Funktionsterm ausrechnen.
Suche dir nun einen Punkt, den du gut vom Funktionsgraphen ablesen kannst und der nicht der Scheitelpunkt ist.
Es bietet sich der Punkt an, da da die Parabel genau die Kästchen trifft.
Setze die Koordinaten des Punktes in die allgemeine Form für die Parabel mit dem Scheitelpunkt ein.
Löse diese Gleichung nach auf!
Der Öffnungsfaktor hat also den Wert .
Aufstellen der Funktionsgleichung
Setze nun den Wert für den Öffnungsfaktor in die allgemeine Funktionsgleichung ein.
Damit erhältst du .
Die Funktionsgleichung der Parabel lautet also .
Hast du eine Frage oder Feedback?
Hier gibt es verschiedene Lösungsansatze: Du kannst z.B: 3 Punkte ablesen und daraus die Funktion bestimmen oder den Öffnungsfaktor der Parabel bestimmen und dann mit einem weiteren Punkt die Funktion ausrechnen.
Bestimme den Funktionsterm einer Parabel mit dem Scheitelpunkt , die durch den Punkt geht.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm aufstellen für Parabeln
Hier berechnen wir den Funktionsterm, indem wir den Öffnungsfaktor bestimmen und mithilfe eines weiteren Punktes den Funktionsterm ausrechnen.
Um den Öffnungsfaktor der Parabel zu bestimmen benötigst du einen Punkt, der nicht der Scheitelpunkt ist. In der Angabe ist schon der Punkt gegeben.
Setze die Koordinaten des Punktes in die allgemeine Form für die Parabel mit dem Scheitelpunkt ein.
Löse diese Gleichung nach auf!
Der Öffnungsfaktor hat also den Wert .
Aufstellen der Funktionsgleichung
Setze nun den Wert für den Öffnungsfaktor in die allgemeine Funktionsgleichung ein.
Damit erhältst du .
Die Funktionsgleichung der Parabel lautet also .
Hast du eine Frage oder Feedback?
Hier gibt es verschiedene Lösungsansatze: Du kannst z.B: 3 Punkte ablesen und daraus die Funktion bestimmen oder den Öffnungsfaktor der Parabel bestimmen und dann mit einem weiteren Punkt die Funktion ausrechnen.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
