Aufgaben zum Aufstellen von Funktionstermen
Hier lernst du einen quadratischen Funktionsterm anhand verschiedenen Daten aufzustellen. Du nutzt gegebene Punkte, Graphen oder Parameter.
- 1
Auf dem Graph der Funktion liegen die folgenden Punkte. Gib für jeden Punkt den Funktionsterm an.
- 2
Der Punkt liegt auf der Parabel der Form . Gib an.
- 3
Gib zu den jeweiligen Scheiteln von verschobenen Normalparabeln den Funktionsterm an.
- 4
Gib den Funktionsterm an, der die verschobene Normalparabel mit Scheitel beschreibt.
- 5
Wie lautet die Gleichung einer nach unten geöffneten Normalparabel mit Scheitel ?
- 6
Bestimme die Funktionsgleichungen der quadratischen Funktionen mit den gegebenen Informationen.
Der Graph der Funktion verläuft durch die Punkte A(1|1), B(3|4), C(5|-1)
Die Funktion besitzt eine doppelte Nullstelle bei x=3 und geht durch den Punkt P(2|0,3).
Die nach unten geöffnete Normalparabel hat den Scheitelpunkt S(2|6).
Die Funktion hat den Scheitelpunkt S(0|-3) und geht durch den Punkt P(1,5|2).
Die Funktion geht durch die Punkte A(2|4), B(3|5), C(-1|13).
- 7
Bestimme jeweils die Scheitelform der unten abgebildeten Parabeln.
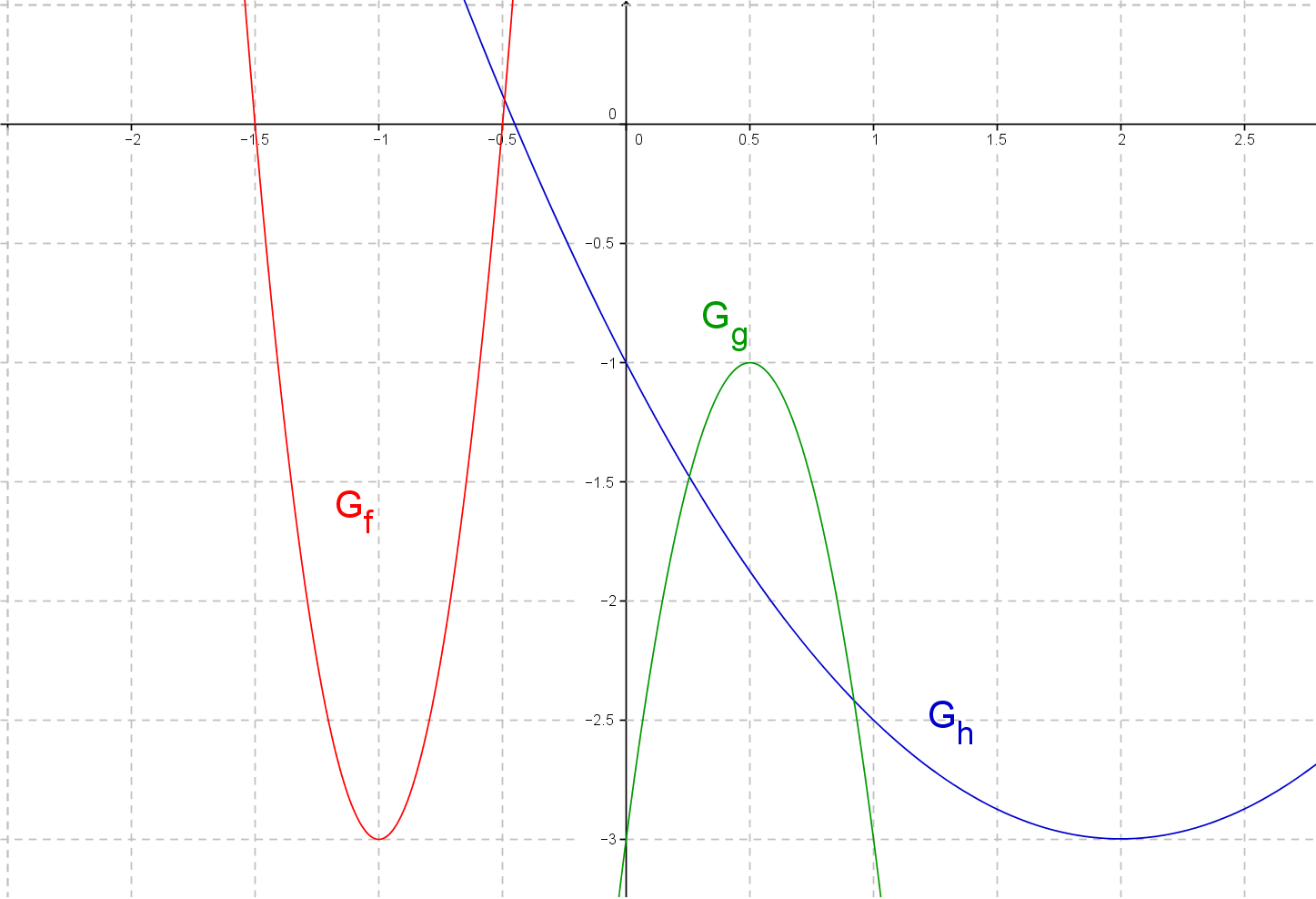
- 8
Der Graph einer ganzrationalen Funktion 2. Grades schneidet die Koordinatenachsen in und in mit .
Bestimme die Funktionsgleichung .
- 9
Bestimme die Funktionsgleichungen von drei verschiedenen quadratischen Funktionen , und nach folgenden Vorgaben: soll nur die Nullstelle haben, und sollen jeweils die beiden Nullstellen und besitzen.
- 10
Für eine Schulaufgabe soll eine quadratische Gleichung mit den Lösungen und entworfen werden; die Gleichung erfüllt diese Vorgabe. Beschreibe, wie man – ausgehend von den Lösungen – auf diese Gleichung kommt.
- 11
Gib die Funktionsterme der gezeichneten Graphen an.
Überlege dir alle drei Funktionsterme, bevor du die Lösung öffnest, da dort alle drei Lösungen sofort erscheinen.
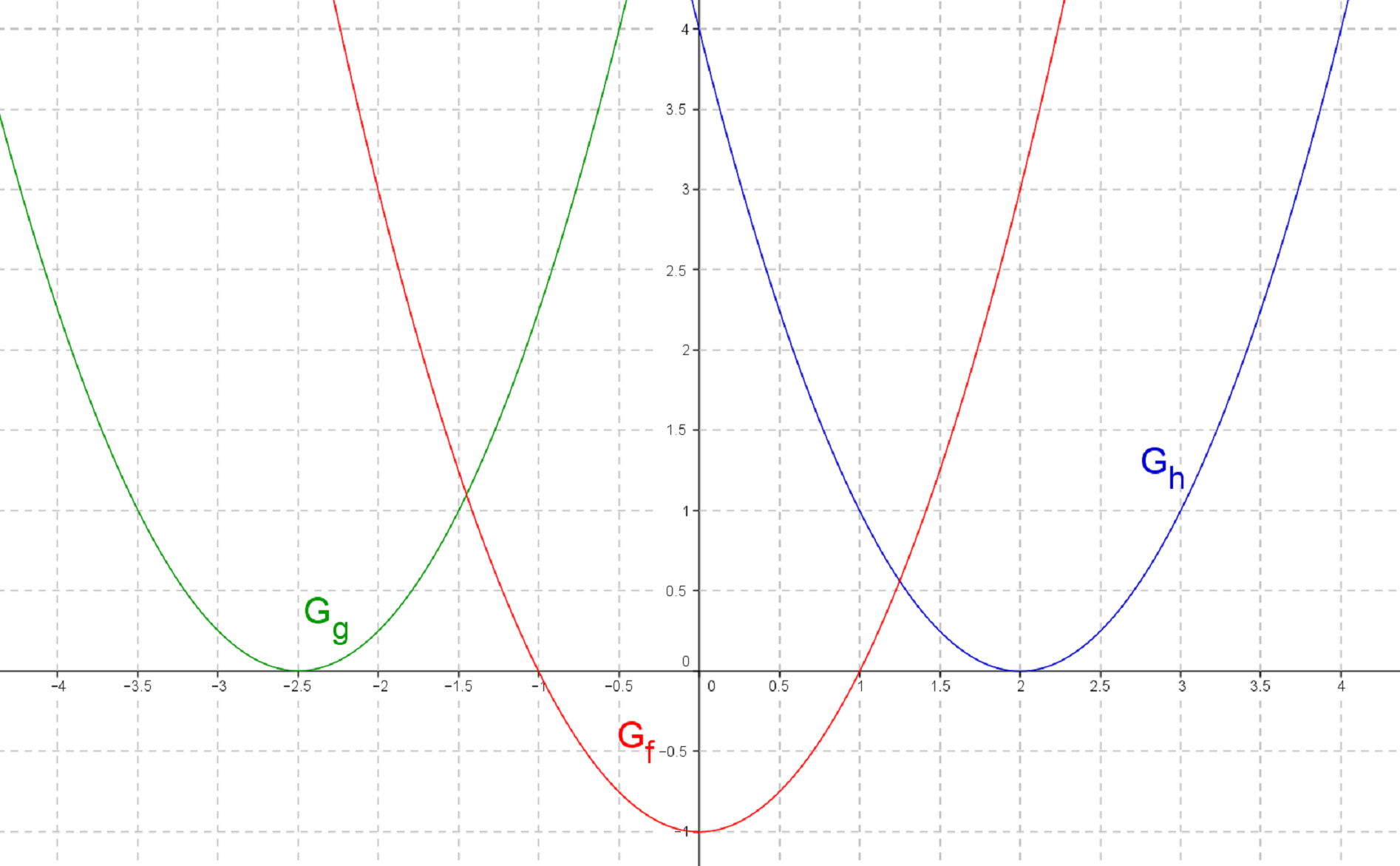
- 12
Bestimme den Öffnungsfaktor und den Funktionsterm der folgenden Parabeln!
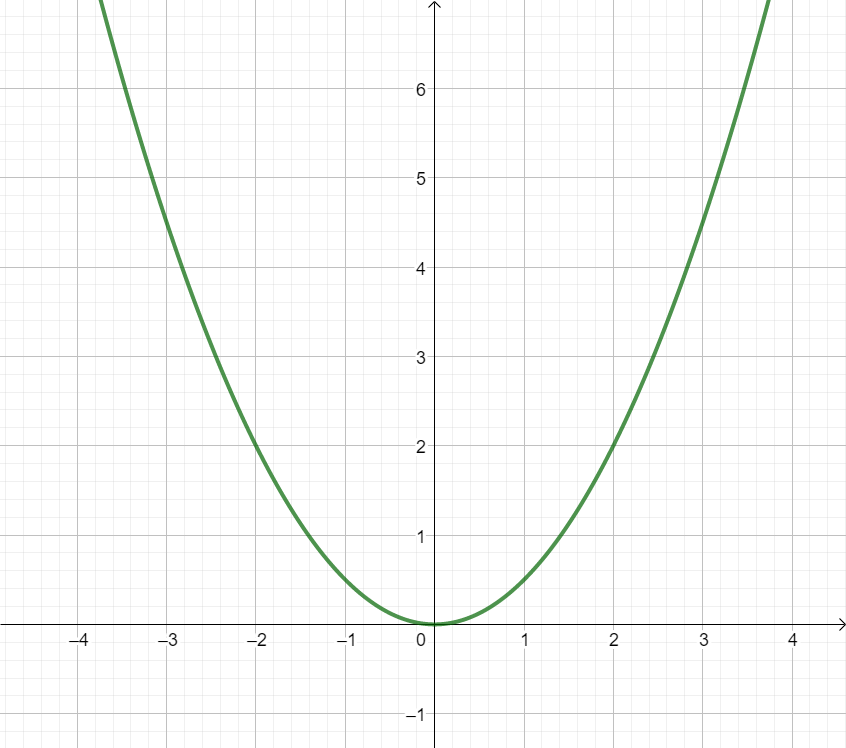
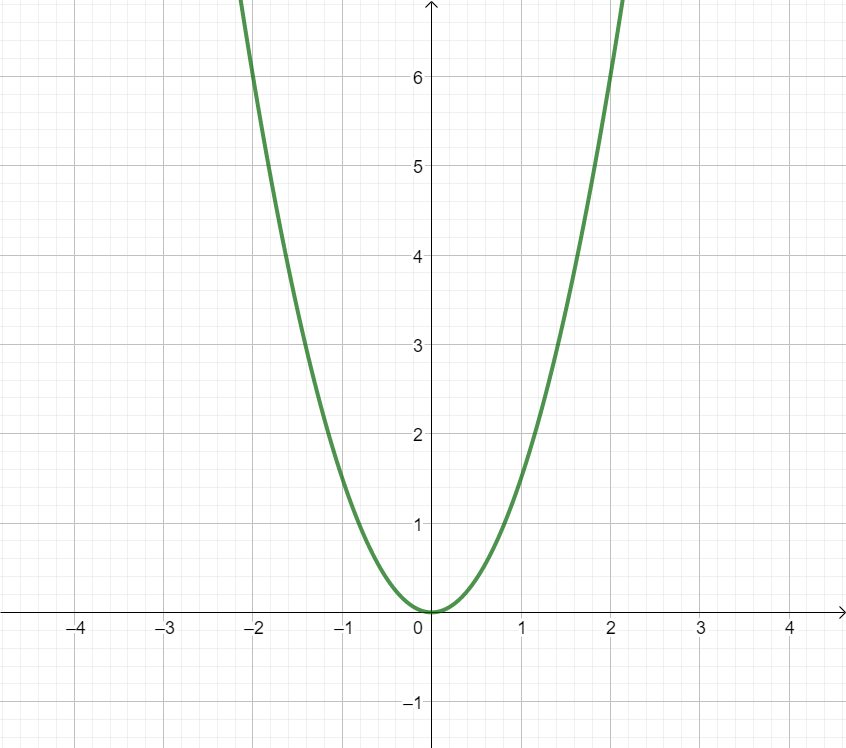
Bestimme den Funktionsterm einer Parabel mit dem Scheitelpunkt , die durch den Punkt geht.
- 13
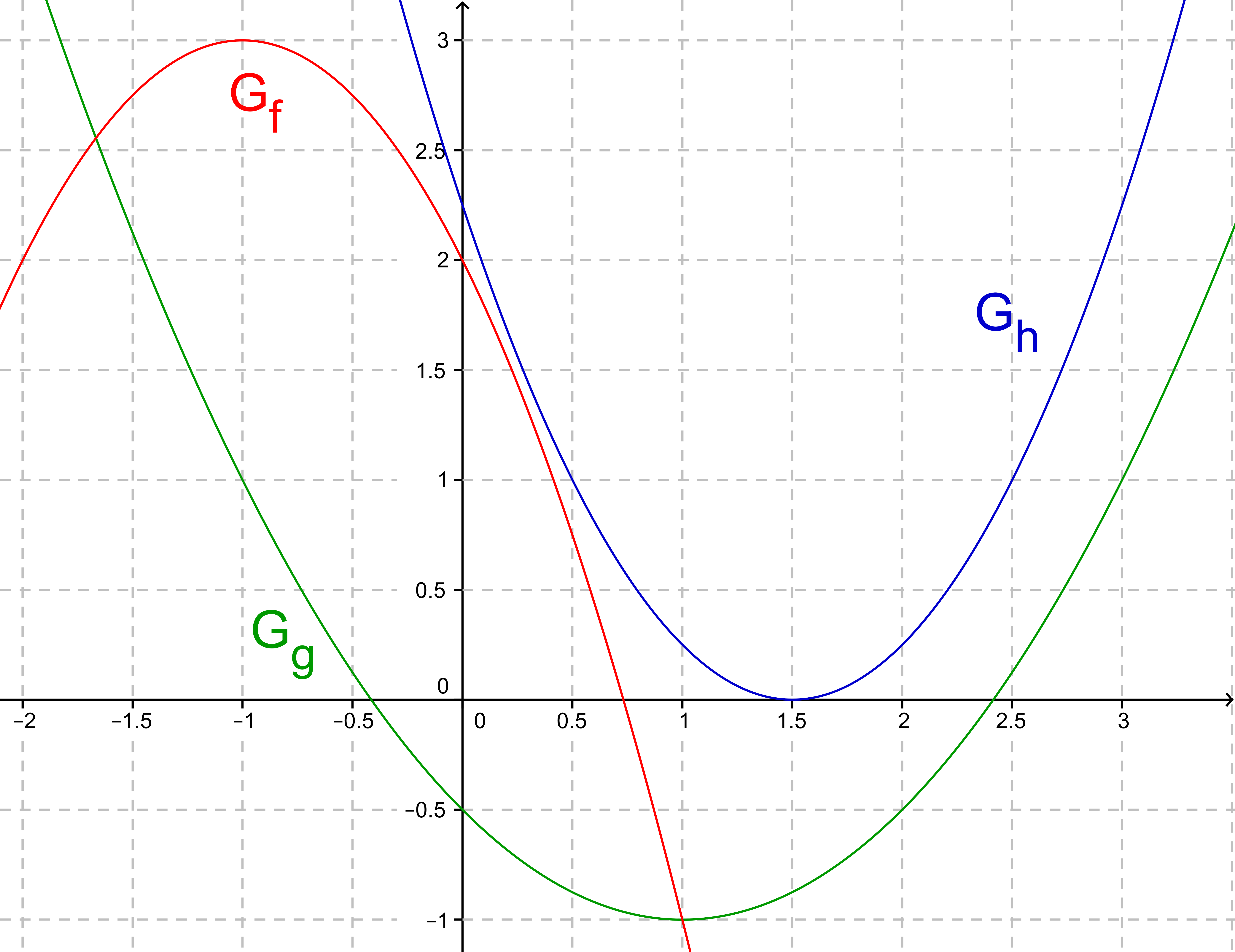
Lies aus nachstehender Abbildung mögliche Funktionsterme der Funktionen , und ab.
Bestimme die Lösungsmenge der Gleichung .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
