Aufgaben zur Methode des Über-Kreuz-Multiplizierens

Hier findest du Aufgaben zu Bruchgleichungen. Lerne, Bruchgleichungen mithilfe des Über-Kreut-Multiplizierens zu lösen!

1
Löse die Bruchgleichung:
$\frac{2 + x}{1 - x} = \frac{3 x}{2 - 3 x}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Über Kreuz multiplizieren
Definitionsmenge bestimmen
Bei jeder Bruchgleichung muss man zu Beginn die Definitionsmenge bestimmen.
$\frac{2 + x}{1 - x} = \frac{3 x}{2 - 3 x}$
Kein Nenner darf $0$ werden.
$1 - x = 0 \Leftrightarrow x = 1$
$2 - 3 x = 0 \Leftrightarrow x = \frac{2}{3}$
Damit lautet die Definitionsmenge: $D = ℚ \ {\frac{2}{3},1}$
Bruchgleichung lösen
Bei dieser Bruchgleichung bietet sich das Verfahren Über Kreuz multiplizieren an.
$\frac{2 + x}{1 - x}$ $=$ $\frac{3 x}{2 - 3 x}$ $\cdot (1 - x) \cdot (2 - 3 x)$
$(2 + x) \cdot (2 - 3 x)$ $=$ $3 x \cdot (1 - x)$
↓
Ausmultiplizieren.
$4 - 6 x + 2 x - 3 x^{2}$ $=$ $3 x - 3 x^{2}$
$4 - 4 x - 3 x^{2}$ $=$ $3 x - 3 x^{2}$ $+ 3 x^{2}$
$4 - 4 x$ $=$ $3 x$ $+ 4 x$
$4$ $=$ $7 x$ $: 7$
$x$ $=$ $\frac{4}{7}$
Da $\frac{4}{7}$ in der Definitionsmenge enthalten ist, lautet die Lösungsmenge:
$𝕃 = {\frac{4}{7}}$

Beim Lösen einer Gleichung der Form $\frac{a}{b} = \frac{c}{d}$ muss man „Über-Kreuz-Multiplizieren“. Das heißt $\frac{a}{b} = \frac{c}{d}$ ist das Gleiche wie $a \cdot d = b \cdot c$ .

Wende dieses Vorgehen bei den folgenden Bruchgleichungen an.

$\frac{3}{2 x + 1} = \frac{2}{2 - x}$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Über-Kreuz-Multiplizieren
Definitionsmenge bestimmen
Zunächst musst du die Definitionsmenge der Gleichung bestimmen.
$\frac{3}{2 x + 1} = \frac{2}{2 - x}$
Keiner der beiden Nenner darf $0$ werden.
Deshalb musst du aus der Definitionsmenge alle Zahlen ausschließen, für die $0$ in einem der Nenner ergeben würde.
Verboten sind hier also:
$2 x + 1 = 0$
$2 - x = 0$
Erste Gleichung lösen!
$2 x + 1$ $=$ $0$ $- 1$
$2 x$ $=$ $- 1$ $: 2$
$x$ $=$ $- \frac{1}{2}$
Zweite Gleichung lösen!
$2 - x$ $=$ $0$ $- 2$
$- x$ $=$ $- 2$ $: (- 1)$
$x$ $=$ $2$
Daher müssen die Zahlen $- \frac{1}{2}$ und $2$ aus der Definitionsmenge der Bruchgleichung ausgeschlossen werden.
Die Definitionsmenge ist $D = ℚ \ {- 0,5; 2}$ , wenn als Grundmenge die Menge $ℚ$ der rationalen Zahlen verwendet wird.
Bruchgleichung lösen
Nun löst du die Bruchgleichung mit der Methode des Über-Kreuz-Multiplizierens:
$\frac{3}{2 x + 1} = \frac{2}{2 - x}$
Über-Kreuz-Multiplizieren! $\frac{a}{b} = \frac{c}{d} \Leftrightarrow a \cdot d = c \cdot b$
$\frac{3}{2 x + 1}$ $=$ $\frac{2}{2 - x}$ $\cdot (2 x + 1) (2 - x)$
$3 \cdot (2 - x)$ $=$ $2 \cdot (2 x + 1)$
↓
Multipliziere die Klammern aus.
$6 - 3 x$ $=$ $4 x + 2$ $- 2 + 3 x$
↓
Löse dann die Gleichung durch Umformen nach $x$ auf.
$4$ $=$ $7 x$ $: 7$
$\frac{4}{7}$ $=$ $x$
Überprüfe jetzt noch, ob $x = \frac{4}{7}$ in der Definitionsmenge enthalten ist. Es gilt $x = \frac{4}{7} \in D$ , also ist die Lösungsmenge $𝕃 = {\frac{4}{7}}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$\frac{x - 2}{3 + x} = \frac{2 x}{2 x - 3}$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Über-Kreuz-Multiplizieren
Definitionsbereich bestimmen
Zunächst musst du die Definitionsmenge der Gleichung bestimmen.
$\frac{x - 2}{3 + x} = \frac{2 x}{2 x - 3}$
Keiner der beiden Nenner darf $0$ werden.
Aus der Definitionsmenge musst du deshalb alle Zahlen ausschließen, für die einer der Nenner $0$ ergeben würde.
Verboten sind hier also:
$3 + x = 0$
$2 x - 3 = 0$
Löse die erste Gleichung!
$3 + x$ $=$ $0$ $- 3$
$x$ $=$ $- 3$
Löse die zweite Gleichung!
$2 x - 3$ $=$ $0$ $+ 3$
$2 x$ $=$ $3$ $: 2$
$x$ $=$ $\frac{3}{2}$
Daher müssen die Zahlen $- 3$ und $\frac{3}{2}$ aus der Definitionsmenge der Bruchgleichung ausgeschlossen werden.
Die Definitionsmenge ist $D = ℚ \ {- 3, \frac{3}{2}}$ , wenn als Grundmenge die Menge $ℚ$ der rationalen Zahlen verwendet wird.
Bruchgleichung lösen
Nun löst du die Bruchgleichung mit der Methode des Über-Kreuz-Multiplizierens:
$\frac{x - 2}{3 + x}$ $=$ $\frac{2 x}{2 x - 3}$ $\cdot (3 + x) (2 x - 3)$
$(x - 2) \cdot (2 x - 3)$ $=$ $2 x \cdot (3 + x)$
↓
Klammern ausmultiplizieren.
$2 x^{2} - 3 x - 4 x + 6$ $=$ $6 x + 2 x^{2}$
↓
Löse nun die Gleichung nach $x$ auf!
$2 x^{2} - 7 x + 6$ $=$ $6 x + 2 x^{2}$ $- 2 x^{2} + 7 x$
$6$ $=$ $13 x$ $: 13$
$\frac{6}{13}$ $=$ $x$
Überprüfe jetzt noch, ob $x = \frac{6}{13}$ in der Definitionsmenge enthalten ist. $x = \frac{6}{13} \in D$ also ist die Lösungsmenge $𝕃 = {\frac{6}{13}}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$1 + \frac{2}{2 x - 1} = \frac{x}{x + 2}$

3
Bestimme die Definitions- und Lösungsmenge der Bruchgleichung.
$\frac{x}{x - 1} = \frac{1}{x - 1}$ .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsmenge
Tipp: Liegt deine Lösung wirklich in der Definitionsmenge?
Definitionsmenge bestimmen
Beide Nenner nehmen für $x = 1$ den Wert $0$ an. Das darf nicht passieren. Deshalb muss man die $1$ aus der Definitionsmenge ausschließen.
Für die Definitionsmenge dieser Gleichung folgt:
$D = ℚ \ {1}$ .
Bruchgleichung lösen
Es bietet sich hier die Strategie "Über Kreuz multiplizieren" an. Hier sind beide Nenner sogar identisch.
$\frac{x}{x - 1} = \frac{1}{x - 1}$ .
$| \cdot (x - 1)$
$\frac{x (x - 1)}{x - 1} = \frac{1 (x - 1)}{x - 1}$ .
Kürzen.
$x = 1$
$1$ ist nicht in der Definitionsmenge enthalten und somit auch nicht in der Lösungsmenge.
Also ist $1$ keine Lösung der Gleichung.
An den zwei Graphen kann man erkennen, dass die Gleichung gar keine Lösung hat. Also gilt für die Lösungsmenge $𝕃 = \emptyset$ .
$f (x) = \frac{x}{x - 1}$
$g (x) = \frac{1}{x - 1}$ .

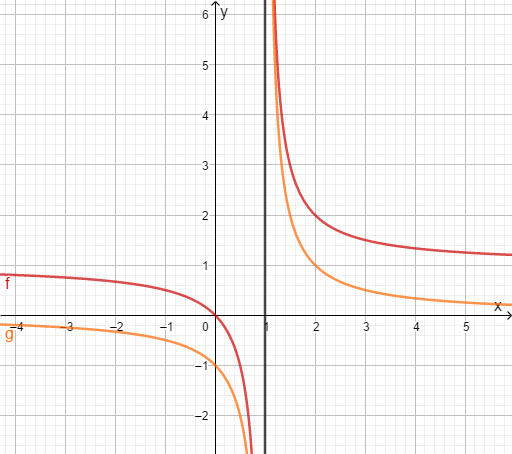
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$1 + \frac{2}{2 x - 1}$	$=$	$\frac{x}{x + 2}$
	↓	Den Summanden $1$ mit $2 x - 1$ erweitern.
$\frac{2 x - 1}{2 x - 1} + \frac{2}{2 x - 1}$	$=$	$\frac{x}{x + 2}$
	↓	Brüche auf der linken Seite addieren.
$\frac{2 x - 1 + 2}{2 x - 1}$	$=$	$\frac{x}{x + 2}$
	↓	Auf der linken Seite den Zähler zusammenfassen.
$\frac{2 x + 1}{2 x - 1}$	$=$	$\frac{x}{x + 2}$	$\cdot (2 x - 1) (x + 2)$
	↓	Nun wendest du die Methode des Über-Kreuz-Multiplizierens an.
$(2 x + 1) \cdot (x + 2)$	$=$	$x \cdot (2 x - 1)$
	↓	Klammern ausmultiplizieren
$2 x^{2} + 4 x + x + 2$	$=$	$2 x^{2} - x$
	↓	Linke Seite zusammenfassen.
$2 x^{2} + 5 x + 2$	$=$	$2 x^{2} - x$	$- 2 x^{2} + x$
	↓	Löse nach $x$ auf.
$6 x + 2$	$=$	$0$	$- 2$
$6 x$	$=$	$- 2$	$: 6$
$x$	$=$	$- \frac{2}{6}$
	↓	Kürzen.
$x$	$=$	$- \frac{1}{3}$

Aufgaben zur Methode des Über-Kreuz-Multiplizierens

Definitionsmenge bestimmen

Bruchgleichung lösen

Definitionsmenge bestimmen

Erste Gleichung lösen!

Zweite Gleichung lösen!

Bruchgleichung lösen

Hast du eine Frage oder Feedback?

Definitionsbereich bestimmen

Löse die erste Gleichung!

Löse die zweite Gleichung!

Bruchgleichung lösen

Hast du eine Frage oder Feedback?

Definitionsbereich bestimmen

Löse die erste Gleichung.

Löse die zweite Gleichung.

Bruchgleichung lösen

Hast du eine Frage oder Feedback?

Definitionsmenge bestimmen

Bruchgleichung lösen

$\frac{2 + x}{1 - x}$	$=$	$\frac{3 x}{2 - 3 x}$	$\cdot (1 - x) \cdot (2 - 3 x)$
$(2 + x) \cdot (2 - 3 x)$	$=$	$3 x \cdot (1 - x)$
	↓	Ausmultiplizieren.
$4 - 6 x + 2 x - 3 x^{2}$	$=$	$3 x - 3 x^{2}$
$4 - 4 x - 3 x^{2}$	$=$	$3 x - 3 x^{2}$	$+ 3 x^{2}$
$4 - 4 x$	$=$	$3 x$	$+ 4 x$
$4$	$=$	$7 x$	$: 7$
$x$	$=$	$\frac{4}{7}$

$\frac{3}{2 x + 1}$	$=$	$\frac{2}{2 - x}$	$\cdot (2 x + 1) (2 - x)$
$3 \cdot (2 - x)$	$=$	$2 \cdot (2 x + 1)$
	↓	Multipliziere die Klammern aus.
$6 - 3 x$	$=$	$4 x + 2$	$- 2 + 3 x$
	↓	Löse dann die Gleichung durch Umformen nach $x$ auf.
$4$	$=$	$7 x$	$: 7$
$\frac{4}{7}$	$=$	$x$

$\frac{x - 2}{3 + x}$	$=$	$\frac{2 x}{2 x - 3}$	$\cdot (3 + x) (2 x - 3)$
$(x - 2) \cdot (2 x - 3)$	$=$	$2 x \cdot (3 + x)$
	↓	Klammern ausmultiplizieren.
$2 x^{2} - 3 x - 4 x + 6$	$=$	$6 x + 2 x^{2}$
	↓	Löse nun die Gleichung nach $x$ auf!
$2 x^{2} - 7 x + 6$	$=$	$6 x + 2 x^{2}$	$- 2 x^{2} + 7 x$
$6$	$=$	$13 x$	$: 13$
$\frac{6}{13}$	$=$	$x$