Gruppe A - lernen mit Serlo!

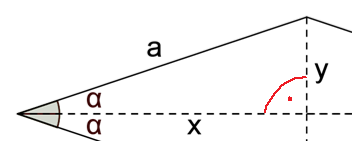
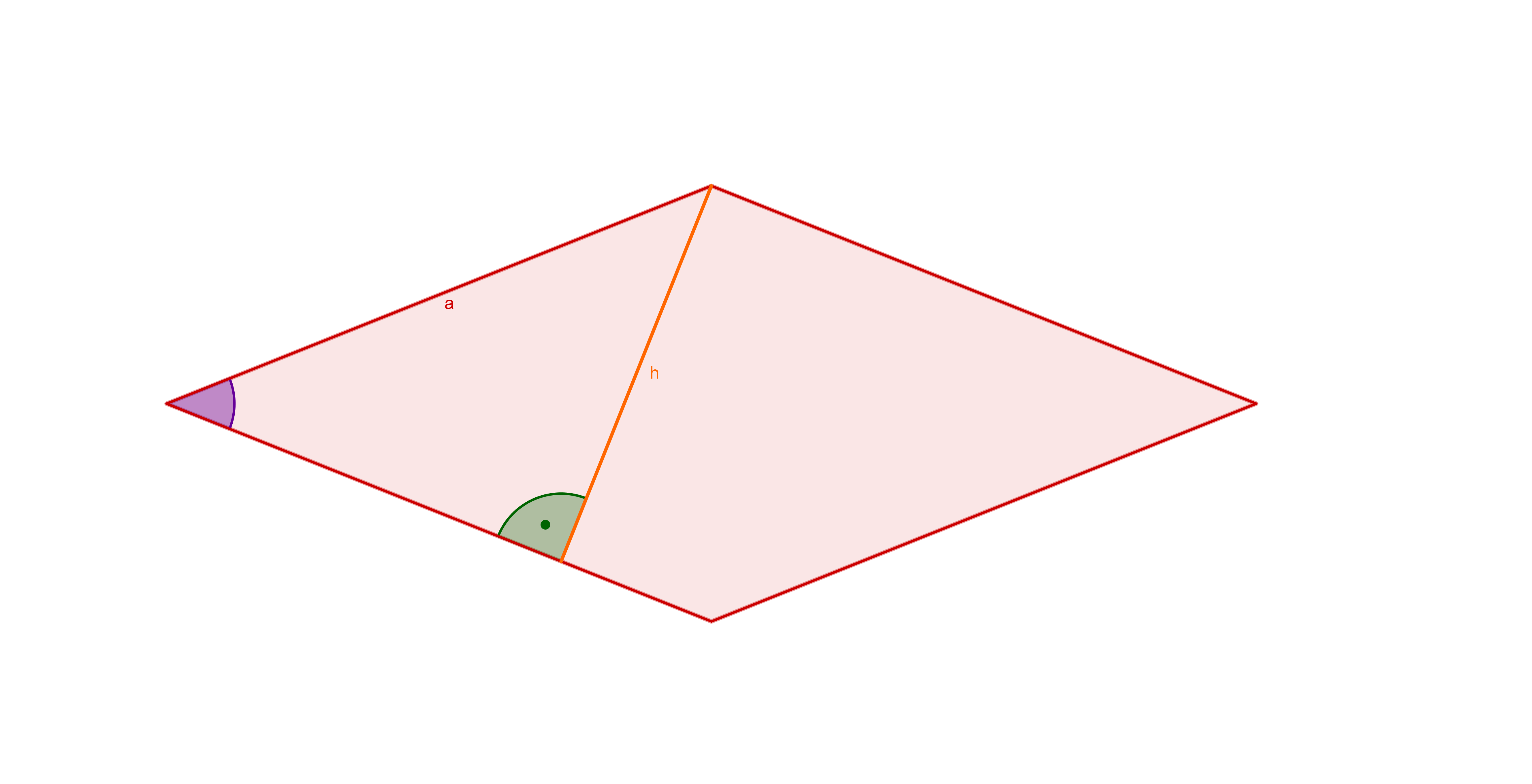
Die Abbildung zeigt eine Raute mit der Seitenlänge $a$ und einem Innenwinkel $2 α$ .

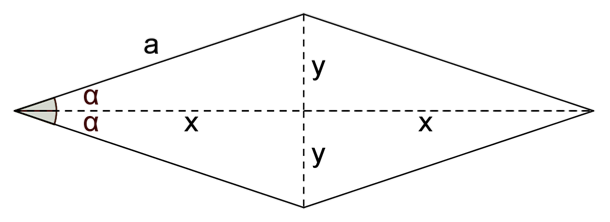
Stellen Sie die Katheten $x$ und $y$ der rechtwinkligen Teildreiecke der Raute mithilfe von $a$ und $α$ dar und zeigen Sie, dass für den Flächeninhalt $A$ der Raute gilt: $A = 2 \cdot a^{2} \cdot \cos (α) \cdot \sin (α)$ .
(2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus, Kosinus und Tangens
Berechnungen mit Sinus und Cosinus
Du betrachtest eines der vier kleinen rechtwinkligen Dreiecke. Ordne als erstes $a$ , $x$ und $y$ die Begriffe Hypotenuse, Gegenkathete und Ankathete im Bezug zum Winkel $α$ zu.
$a$ ist die Hypotenuse, weil sie gegenüber vom rechten Winkel liegt.
$x$ ist die Ankathete, da sie an dem Winkel $α$ liegt.
$y$ ist die Gegenkathete, da sie gegenüber des Winkel $α$ liegt.
Du sollst $x$ und $y$ durch $a$ und $α$ ausdrücken. Dafür kannst du die Formeln für Sinus und Kosinus im rechtwinkligen Dreieck nutzen:
$\sin (α) = \frac{Gegenkathete}{Hypotenuse}$ und
$\cos (α) = \frac{Ankathete}{Hypotenuse}$
Du kannst die gegebenen Bezeichungen in die Formeln einsetzen und jeweils nach $x$ und $y$ auflösen.
$\begin{array}{rcll} \sin (α) & = & \frac{y}{a} & | \cdot a \\ y & = & \sin (α) \cdot a \end{array}$
und genauso
$\begin{array}{rcl} \cos (α) & = & \frac{x}{a} & | \cdot a \\ x & = & \cos (α) \cdot a \end{array}$
Flächeninhalt der Raute
Die Raute besteht aus vier gleich großen Dreiecken mit Grundseite $x$ und Höhe $y$ . Also kann man für den Flächeninhalt der Raute den Flächeninhalt des Dreiecks mit $4$ multiplizieren.
$\begin{array}{rcl} A & = & 4 \cdot A_{k l e i n e s D r e i e c k} \\ = & 4 \cdot \frac{1}{2} \cdot x \cdot y \\ = & 2 \cdot x \cdot y \end{array}$
Nun kannst du $x$ und $y$ durch die Terme ersetzen, die du oben gefunden hast.
$\begin{array}{rcl} A & = & 2 \cdot \cos (α) \cdot a \cdot \sin (α) \cdot a \\ = & 2 \cdot a^{2} \cdot \cos (α) \cdot \sin (α) \end{array}$
Damit hast du den Term erhalten, der in der Aufgabenstellung gegeben ist.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Zeigen Sie die Gültigkeit der Gleichung
$\sin (2 α) = 2 \cdot \cos (α) \cdot \sin (α)$
indem Sie den Flächeninhalt der Raute erneut berechnen, nun aber mithilfe der Formel für den Flächeninhalt eines Parallelogramms. (1 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus, Kosinus und Tangens
Du sollst den Flächeninhalt des Parallelogramms berechnen. Dazu musst du die Grundseite mit der Höhe multiplizieren. Die Höhe kennst du noch nicht.
Du weißt allerdings, dass sie immer senkrecht auf der Grundseite steht. Damit erhältst du ein rechtwinkliges Dreieck mit dem lilanen Winkel $2 α$ , der Hypotenuse $a$ (die gegenüber des rechten Winkels liegende Rautenseite) und als Gegenkathete die gesuchte Höhe $h$ .
Das heißt, du kannst wieder den Sinus verwenden.
$\sin (2 α) = \frac{Gegenkathete}{Hypotenuse} = \frac{h}{a}$
Nach $h$ umgestellt ergibt sich:
$h = \sin (2 α) \cdot a$
Nun kannst du den Flächeninhalt des Parallelogramms berechnen:
$\begin{array}{rcl} A_{P a r a l l e l o g r a m m} & = & h \cdot a \\ = & \sin (2 α) \cdot a \cdot a \\ = & a^{2} \cdot \sin (2 α) \end{array}$
Als nächstes kannst du die beiden Varianten aus a) und b), den Flächeninhalt zu berechnen gleich setzen und nach $\sin (2 α)$ umstellen.
$\begin{array}{rcl} a^{2} \cdot \sin (2 α) & = & 2 \cdot a^{2} \cdot c o s (α) \cdot s i n (α) & | : a^{2} \\ \sin (2 α) & = & 2 \cdot \cos (α) \cdot \sin (α) \end{array}$
Jetzt hast du die gewünschte Gleichung erhalten und du bist fertig.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Berechnungen mit Sinus und Cosinus

Flächeninhalt der Raute

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?