Gruppe A

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Vereinfachen Sie so weit wie möglich. (1 BE)
$a⁶ (-2a)³=$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
Löse zuerst die Klammer $(-2a)^3$ auf.
$a^6\cdot(-2a)^3= a^6 \cdot (-2) ^3 \cdot a^3$
Fasse $a^6$ und $a^3$ mit Hilfe der Potenzgesetze zusammen.
$a^6\cdot (-2)^3\cdot a^3= -8\cdot a^9$
Löse zuerst die Klammer auf
Vereinfache

Sophie hat mithilfe einer Schnur den Umfang U des abgebildeten Baumstamms bestimmt und daraus den zugehörigen Radius r berechnet. Sie hat r = 0,5 m erhalten.

Geben Sie einen Term an, mit dem man $r$ aus $U$ berechnen kann. (1 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Umfang eines Kreises
Umstellung nach r
Du sollst $r$ aus $U$ berechnen. Also überlegst du dir zuerst die Formel für den Umfang eines Kreises, da der Baum näherungsweise einen Kreis als Querschnitt hat:
$U=2\pi r$
Du stellst fest, dass praktischerweise $r$ in dieser Formel vorkommt und stellst danach um:
$r=\displaystyle\frac{U}{2\pi}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Schätzen Sie ab, welches Volumen der Teil des Baumstamms hat, der in der Abbildung zu sehen ist. (2 BE)

Eine 120-jährige Buche hat einen Stamm mit einer Trockenmasse von 1,9t. Für den Aufbau ihres Stamms hat sie der Atmosphäre im Laufe ihres bisherigen Lebens 3,5t $CO_2$ entnommen. Wie viele kg $CO_2$ sind dies durchschnittlich pro Jahr? Kreuzen Sie nur den richtigen Term an. (1 BE)
- $\displaystyle \frac{3{,}5 \cdot 1000}{120}$
- $\displaystyle \frac{120 \cdot 1000}{1{,}9}$
- $\displaystyle \frac{120}{1{,}9 \cdot 1000}$
- $\displaystyle \frac{120}{1{,}9 \cdot 100}$
- $\displaystyle \frac{3{,}5 \cdot 120}{1000}$
- $\displaystyle \frac{3{,}5 \cdot 100}{120}$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umrechnen
Kohlenstoffdioxidverbrauch pro Jahr
Gefragt sind nach den kg $CO_2$ durchschnittlich pro Jahr. Wenn du diese Frage in eine Rechnung übersetzt, musst du "Gesamtmenge $CO_2$ in kg" geteilt durch "Anzahl Jahre" rechnen. Beachte, dass dir die Gesamtmenge in Tonnen angegeben ist und du in Kilogramm umrechnen musst.
$\displaystyle\frac{3{,}5 \text{ t}}{120}=\frac{3{,}5 \cdot 1000 \text{ kg}}{120}$
Also ist der Term $\displaystyle\frac{3{,}5 \cdot 1000 }{120}$ richtig.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

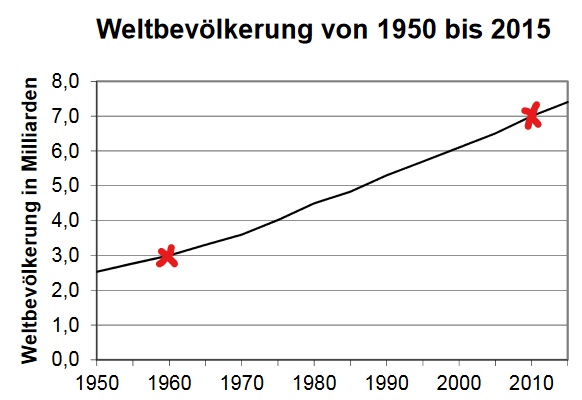
Das Diagramm zeigt die Entwicklung der Weltbevölkerung im Zeitraum von 1950 bis 2015.

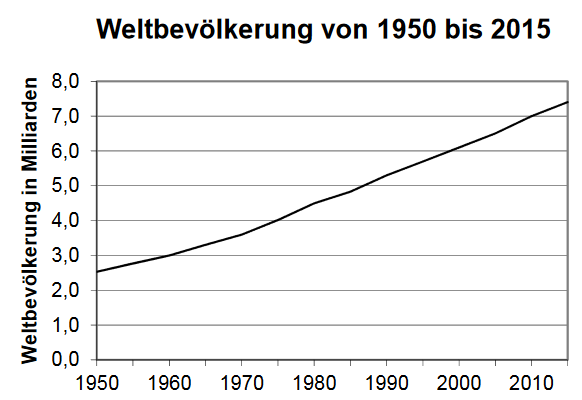
Ermitteln Sie, um wie viele Millionen Menschen die Weltbevölkerung laut Diagramm zwischen 1960 und 2010 durchschnittlich pro Jahr zugenommen hat. (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Diagramme auswerten
Um den durchschnittlichen Zuwachs pro Jahr zu berechnen, musst du den Gesamtzuwachs durch die Gesamtzahl der Jahre teilen.
Für den Zuwachs zwischen 1960 und 2010 musst du die Werte für die Größe der Weltbevölkerung ablesen. 1960 waren es $3{,}0$ Milliarden Menschen und 2010 $7{,}0$ Milliarden.
Nun kannst du den Zuwachs und die Anzahl der Jahre ausrechen, indem du jeweils Endwert minus Anfangswert rechnest.
Zuwachs: $7{,}0-3{,}0=4{,}0$ Milliarden
Anzahl der Jahre: $2010-1960=50$ Jahre
Für den durchschnittlichen Zuwachs teilst du den Zuwachs durch die Gesamtjahre. Beachte, dass du es in Millionen Menschen pro Jahr angeben sollst und nicht in Milliarden!
$\displaystyle\frac{4{,}0 \text{ Milliarden}}{50}=\frac{4000 \text{ Millionen}}{50}=\frac{400\text{ Millionen}}{5}=80\text{ Millionen}$
Der durchschnittliche Zuwachs hat also $80$ Millionen Menschen pro Jahr betragen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Die nachstehende Tabelle zeigt für einige ausgewählte Jahre die Zahl der von Nahrungsmittelknappheit betroffenen Menschen weltweit.
$\def\arraystretch{1.25} \begin{array}{|l|c|c|c|}\hline\textrm{Jahr} & 1970 & 1990 & 2005\\ \hline\textrm{Zahl der von Nahrungsmittel-}& 870 & 840 & 870 \\\textrm{knappheit Betroffenen in Millionen}\\ \hline\end{array}$
In einem Zeitungsartikel ist zu lesen: „1970 waren ungefähr 25 % der Weltbevölkerung von Nahrungsmittelknappheit betroffen. 2005 war dieser Prozentsatz nur noch ungefähr halb so groß.“
Begründen Sie, dass diese beiden Aussagen mit den vorliegenden Daten in Einklang stehen. (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozentsatz
Bestätigung der Zahl der von Nahrungsknappheit Betroffenen
Um die Aussage bestätigen zu können, musst du zuerst den Prozentsatz für von Nahrungsmittelknappheit Betroffenen 1970 ausrechnen.
Die Prozentformel ist $\text{Prozentsatz}\cdot\text{Grundwert}=\text{Prozentwert}$ . Nachdem du den Prozentsatz herausfinden willst, musst du danach umstellen:
$\text{Prozentsatz}=\displaystyle\frac{\text{Prozentwert}}{\text{Grundwert}}$
Jetzt musst du dir überlegen, was in der Aufgabe dem Grundwert und was dem Prozentwert entspricht. Der Grundwert ist die gesamte Menschheit 1970, also, aus dem Diagramm abgelesen, ca. $3{,}5$ Milliarden Menschen. Der Prozentwert sind die von Nahrungsmittelknappheit Betroffenen 1970, also $870$ Millionen Menschen (siehe Tabelle). Nun kannst du einsetzen. Achte dabei darauf, dass du nur gleiche Einheiten durcheinander teilen darfst.
$\text{Prozentsatz}=\displaystyle\frac{\text{Prozentwert}}{\text{Grundwert}}=\frac{870 \text{ Mio}}{3{,}5\text{ Mrd}}=\frac{870 \text{ Mio}}{3500\text{ Mio}}\approx 0{,}25 = 25 \%$
Falls du Schwierigkeiten mit der Division ohne Taschenrechner hattest, klicke hier.
Jetzt konntest du die erste Aussage, dass 1970 25 % der Weltbevölkerung von Hunger betroffen waren, bestätigen.
Als nächstes schaust du dir an, was sich 2005 im Vergleich zu 1970 geändert hat: Der Prozentwert ist gleich geblieben ( $870$ Mio), aber der Grundwert hat sich von $3{,}5$ Mrd Menschen auf $6{,}5$ Mrd Menschen vergrößert, hat sich also fast verdoppelt. Nun betrachtest du die Formel für den Prozentsatz ein weiteres Mal:
$\text{Prozentsatz}=\displaystyle\frac{\text{Prozentwert}}{\text{Grundwert}}$
Du erkennst, dass der Grundwert im Nenner steht. Wenn sich dieser verdoppelt, halbiert sich deswegen der Prozentsatz. Damit hast du auch den zweiten Teil der Aussage bestätigt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Der Flächeninhalt der Ackerfläche der Erde wurde 2010 auf 1,4 $\cdot$ 10 $^{13}$ m² geschätzt. Wie viele Quadratmeter dieser Fläche entfielen im Jahr 2010 bei gleichmäßiger Aufteilung auf jeden Erdenbürger? (1 BE)

Die dargestellte Figur ist symmetrisch zur y-Achse und besteht aus Teilen von Parabeln.

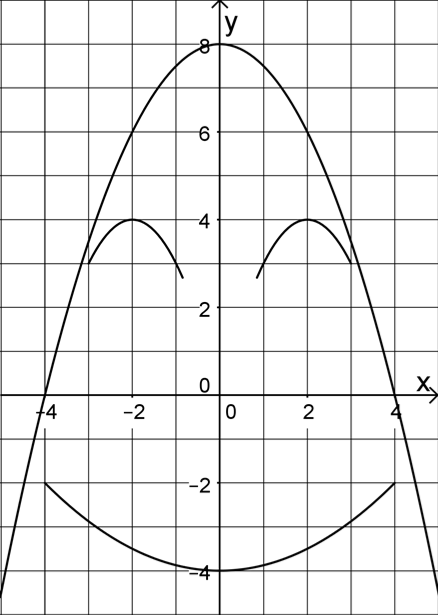
Die zu einem „Auge“ gehörende Funktion hat die Gleichung y=-(x-2)²+4. Geben Sie die Gleichung der zum anderen Auge gehörenden Funktion an. (1 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitel
Funktion des zweiten Auges
Als erstes musst du herausfinden, von welchem Auge du die Gleichung aufstellen sollst, also von welchem Auge sie dir bereits gegeben ist. Dafür liest du den Scheitel ab: $S(2|4)$ . Das ist der Scheitel der rechten Parabel, also musst du nun noch die Gleichung der linken Parabel aufstellen.
Die Scheitelform einer Parabel ist $y=a(x-d)^2+e$ . Du musst nun die einzelnen Parameter herausfinden.
$a=-1$
Die Parabel ist nach unten geöffnet, deswegen ist $a$ negativ. $|a|=1$ , da die Parabel weder gestreckt noch gestaucht ist. Alternativ kannst du dir auch überlegen, dass $a$ genauso groß sein muss, wie bei der angegebenen Parabel, da die Parabel links die Parabel von rechts gespiegelt an der $y$ -Achse ist.
$d=-2$
Die $x$ -Koordinate des Scheitels ist $-2$ .
$e=4$
Die $y$ -Koordinate des Scheitels ist $4$ .
Damit ist die gesuchte Gleichung für das Auge:
$y=-(x-(-2))^2+4=-(x+2)^2+4$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Der „Mund“ ist Teil der Parabel mit der Gleichung y= $\frac18$ x²-4. Berechnen Sie die x-Koordinaten der Schnittpunkte dieser Parabel mit der x-Achse. (2 BE)

Wählen Sie aus der folgenden Liste diejenige Funktionsgleichung aus, die zum „Umriss“ der Figur gehört. (1 BE)
- $y = 8 - \frac{1}{2}x^2$
- $y = -4x^2 + 8$
- $y = 4-\frac{1}{4}x^2$
- $y = \frac{1}{2}(4-x)^2$
Funktion des Umrisses
Die Scheitelform einer Parabel hat allgemein folgende Form: $y=a(x-d)^2+e$ . Du musst nun die einzelnen Parameter herausfinden.
$a=-\frac12$
Die Parabel ist nach unten geöffnet, deswegen ist $a$ negativ. $|a|=\frac12$ , weil die Öffnung im Vergleich zur Normalparabel doppelt so breit ist. Das kannst du zum Beispiel daran erkennen, dass du vom Scheitel nicht eine Einheit nach rechts und eine Einheit nach unten gehst, um wieder einen Punkt der Parabel zu erhalten, sondern bei einer Einheit nach rechts nur eine halbe Einheit nach unten, also genau die Hälfte.
$d=0$
Die Parabel ist in $x$ -Richtung nicht verschoben, weil der Scheitel auf der $y$ -Achse liegt.
$e=8$
Die $y$ -Koordinate des Scheitels ist $8$ .
Damit erhältst du für die Parabel nach dem Einsetzen der Parameter
$y=-\frac12(x-0)^2+8=-\frac12 x^2+8=8-\frac12x^2$ .
Also ist die letzte Antwortmöglichkeit $y=8-\frac12x^2$ richtig.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Gegeben ist die Bruchgleichung $\dfrac{x}{x+3}+2=\dfrac{1}{x+3}$ über der Grundmenge $\mathbb{R}$ .

Begründen Sie, dass $x=-3$ kein Element der Definitionsmenge der Bruchgleichung ist. (1 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsmenge
Überlege dir dazu, wann ein Bruch nicht definiert ist. Man darf bei Brüchen nicht durch Null teilen, also darf der Nenner nie Null werden. Wann wird der Nenner hier Null?
$x+3=0$
Wenn du diese Gleichung umstellst, siehst du, dass bei $x=-3$ der Nenner Null wäre und du das deswegen nicht in die Gleichung einsetzen darfst. Deshalb ist $-3$ nicht Teil der Definitionsmenge.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Berechnen Sie die Lösung der Bruchgleichung. (2 BE)

6
Eine Urne enthält acht rote und zwei blaue Kugeln, die sich ansonsten nicht voneinander unterscheiden. Lukas behauptet: „Die Wahrscheinlichkeit dafür, aus dieser Urne zuerst eine rote und dann eine blaue Kugel zu ziehen, beträgt $\frac8{10}\cdot \frac29$ .“ Erläutern Sie, woran man erkennen kann, dass Lukas dabei voraussetzt, dass die erste gezogene Kugel nicht wieder in die Urne zurückgelegt wird. (1 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Urnenmodell
Für die Gesamtwahrscheinlichkeit darfst du die Wahrscheinlichkeit für die erste Kugel mit der Wahrscheinlichkeit für die zweite Kugel multiplizieren.
Überlege dir als erstes, was die Wahrscheinlichkeit für die erste Kugel ist. Du hast $10$ Kugeln und möchtest eine rote Kugel ziehen. Es gibt insgesamt $8$ rote Kugeln, also ist die Wahrscheinlichkeit:
$\displaystyle\frac{\text{passende Kugeln}}{\text{gesamte Kugeln}}=\frac8{10}$
Genauso kannst du für die zweite Kugel vorgehen: Es gibt insgesamt $10$ Kugeln (die erste Kugel wird zurückgelegt) oder $9$ Kugeln (die erste Kugel wird nicht zurückgelegt). In beiden Fällen gibt es $2$ blaue Kugeln, also ist die Wahrscheinlichkeit eine blaue Kugel zu ziehen
$\displaystyle\frac{\text{passende Kugeln}}{\text{gesamte Kugeln}}=\frac2{10}$ oder $\displaystyle\frac{\text{passende Kugeln}}{\text{gesamte Kugeln}}=\frac2{9}$ .
Lukas Term ist $\displaystyle\frac8{10}\cdot \frac29$ , also geht er davon aus, dass die erste Kugel nicht zurückgelegt wird, weil bei ihm die zweite Wahrscheinlichkeit $\displaystyle\frac29$ ist.
7
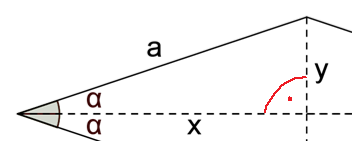
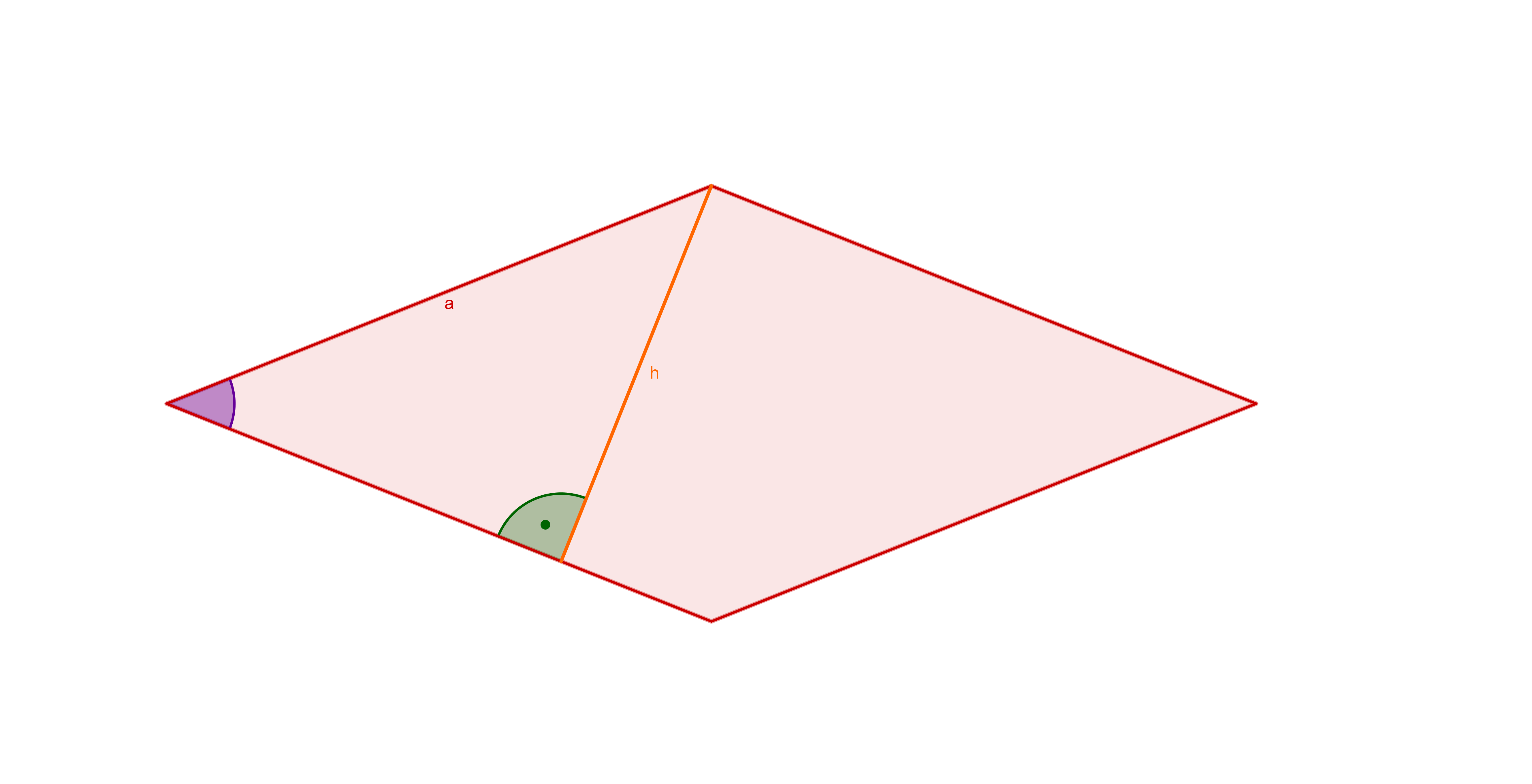
Die Abbildung zeigt eine Raute mit der Seitenlänge $a$ und einem Innenwinkel $2\alpha$ .
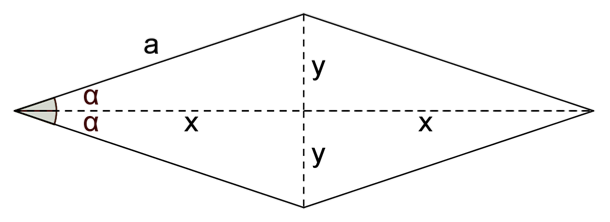
1. Stellen Sie die Katheten $x$ und $y$ der rechtwinkligen Teildreiecke der Raute mithilfe von $a$ und $\alpha$ dar und zeigen Sie, dass für den Flächeninhalt $A$ der Raute gilt: $A= 2 \cdot a^2 \cdot \cos(\alpha) \cdot \sin(\alpha)$ .
  (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus, Kosinus und Tangens
  Berechnungen mit Sinus und Cosinus
  Du betrachtest eines der vier kleinen rechtwinkligen Dreiecke. Ordne als erstes $a$ , $x$ und $y$ die Begriffe Hypotenuse, Gegenkathete und Ankathete im Bezug zum Winkel $\alpha$ zu.
  $a$ ist die Hypotenuse, weil sie gegenüber vom rechten Winkel liegt.
  $x$ ist die Ankathete, da sie an dem Winkel $\alpha$ liegt.
  $y$ ist die Gegenkathete, da sie gegenüber des Winkel $\alpha$ liegt.
  Du sollst $x$ und $y$ durch $a$ und $\alpha$ ausdrücken. Dafür kannst du die Formeln für Sinus und Kosinus im rechtwinkligen Dreieck nutzen:
  $\sin(\alpha)=\dfrac{\text{Gegenkathete}}{\text{Hypotenuse}}$ und
  $\cos(\alpha)=\dfrac{\text{Ankathete}}{\text{Hypotenuse}}$
  Du kannst die gegebenen Bezeichungen in die Formeln einsetzen und jeweils nach $x$ und $y$ auflösen.
  $\def\arraystretch{1.25} \begin{array}{rcll}\sin(\alpha)&=&\displaystyle\frac{y}{a} &\vert \cdot a \\ y&=&\sin(\alpha)\cdot a \end{array}$
  und genauso
  $\def\arraystretch{2} \begin{array}{rcl}\cos(\alpha)&=&\dfrac{x}{a} &\vert\cdot a\\ x&=&\cos(\alpha)\cdot a \end{array}$
  Flächeninhalt der Raute
  Die Raute besteht aus vier gleich großen Dreiecken mit Grundseite $x$ und Höhe $y$ . Also kann man für den Flächeninhalt der Raute den Flächeninhalt des Dreiecks mit $4$ multiplizieren.
  Nun kannst du $x$ und $y$ durch die Terme ersetzen, die du oben gefunden hast.
  Damit hast du den Term erhalten, der in der Aufgabenstellung gegeben ist.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Zeigen Sie die Gültigkeit der Gleichung
  indem Sie den Flächeninhalt der Raute erneut berechnen, nun aber mithilfe der Formel für den Flächeninhalt eines Parallelogramms. (1 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus, Kosinus und Tangens
  Du sollst den Flächeninhalt des Parallelogramms berechnen. Dazu musst du die Grundseite mit der Höhe multiplizieren. Die Höhe kennst du noch nicht.
  Du weißt allerdings, dass sie immer senkrecht auf der Grundseite steht. Damit erhältst du ein rechtwinkliges Dreieck mit dem lilanen Winkel $2\alpha$ , der Hypotenuse $a$ (die gegenüber des rechten Winkels liegende Rautenseite) und als Gegenkathete die gesuchte Höhe $h$ .
  Das heißt, du kannst wieder den Sinus verwenden.
  Nach $h$ umgestellt ergibt sich:
  Nun kannst du den Flächeninhalt des Parallelogramms berechnen:
  Als nächstes kannst du die beiden Varianten aus a) und b), den Flächeninhalt zu berechnen gleich setzen und nach $\sin(2\alpha)$ umstellen.
  Jetzt hast du die gewünschte Gleichung erhalten und du bist fertig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle V$	$=$	$\displaystyle \pi r^2\cdot h$
	$≈$	$\displaystyle 3\cdot0{,}5m^2\cdot5m$
	$=$	$\displaystyle 15\cdot0{,}25$
	$=$	$\displaystyle 3{,}75m^3$
	$≈$	$\displaystyle 4m^3$

$\displaystyle \frac{1{,}4\cdot10^{13}}{7{,}0\cdot10^9}$	$=$
	↓	Du führst nun bei $1{,}4= 14 \cdot 10^{-1}$ eine Kommaverschiebung durch, um nur noch ganze Zahlen und Zehnerpotenzen zu erhalten.
	$=$	$\displaystyle \frac{14\cdot10^{-1}\cdot10^{13}}{7\cdot10^9}$
	↓	Du fasst $10^{-1}\cdot 10^{13}$ mit Hilfe der Potenzgesetze zusammen und kürzt mit $7$ .
	$=$	$\displaystyle \frac{2\cdot10^{12}}{10^9}$
	↓	Als letztes kürzt du die Zehnerpotenzen.
	$=$	$\displaystyle 2\cdot10^3$

$\displaystyle \frac{1}{8}x^2-4$	$=$	$\displaystyle 0$
	↓	Nun musst du nach $x$ auflösen. Dazu addierst du erst $4$ auf beiden Seiten.
$\displaystyle \frac{1}{8}x^2$	$=$	$\displaystyle 4$
	↓	Nun multiplizierst du mit $8$ oder dividierst durch $\frac{1}{8}$ , was beides gleich ist.
$\displaystyle x^2$	$=$	$\displaystyle 32$
	↓	Nun ziehst du die Wurzel. Achte darauf, dass sowohl die positive als auch die negative Lösung möglich ist.
$\displaystyle x$	$=$	$\displaystyle \pm\sqrt{32}$
	↓	Als letztes kannst du noch die Wurzel vereinfachen.
$\displaystyle x$	$=$	$\displaystyle \pm\sqrt{16\cdot2}$
$\displaystyle x$	$=$	$\displaystyle \pm4\sqrt{2}$

$\displaystyle \dfrac{x}{x+3}+2$	$=$	$\displaystyle \dfrac{1}{x+3}$
	↓	Als erstes musst du Bruchgleichungen mit dem Hauptnenner multiplizieren, um eine normale Gleichung zu erhalten. Den Hauptnenner kannst du hier einfach als den Nenner beider Brüche ablesen: $x+3$
$\displaystyle \dfrac{x\cdot\left(x+3\right)}{x+3}+2\cdot\left(x+3\right)$	$=$	$\displaystyle \dfrac{1\cdot\left(x+3\right)}{x+3}$
	↓	Nun kannst du die Nenner kürzen.
$\displaystyle x+2\cdot\left(x+3\right)$	$=$	$\displaystyle 1$
	↓	Jetzt musst du die Klammern ausmultiplizieren.
$\displaystyle x+2x+6$	$=$	$\displaystyle 1$
	↓	Nun bringst du alle $x$ auf eine Seite und alle Zahlen auf die andere Seite.
$\displaystyle 3x$	$=$	$\displaystyle -5$
$\displaystyle x$	$=$	$\displaystyle -\frac{5}{3}$

Gruppe A

Umstellung nach r

Hast du eine Frage oder Feedback?

Schätzen des Volumens

Hast du eine Frage oder Feedback?

Kohlenstoffdioxidverbrauch pro Jahr

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Bestätigung der Zahl der von Nahrungsknappheit Betroffenen

Hast du eine Frage oder Feedback?

Fläche pro Mensch

Hast du eine Frage oder Feedback?

Funktion des zweiten Auges

Hast du eine Frage oder Feedback?

Nullstellenberechnung einer Parabel

Hast du eine Frage oder Feedback?

Funktion des Umrisses

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Berechnungen mit Sinus und Cosinus

Flächeninhalt der Raute

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?