Maximale Definitionsmenge einer Bruchgleichung

Die maximale Definitionsmenge einer Bruchgleichung gibt an, welche Werte für die Variable eingesetzt werden dürfen.

Nenner darf nicht 0 sein

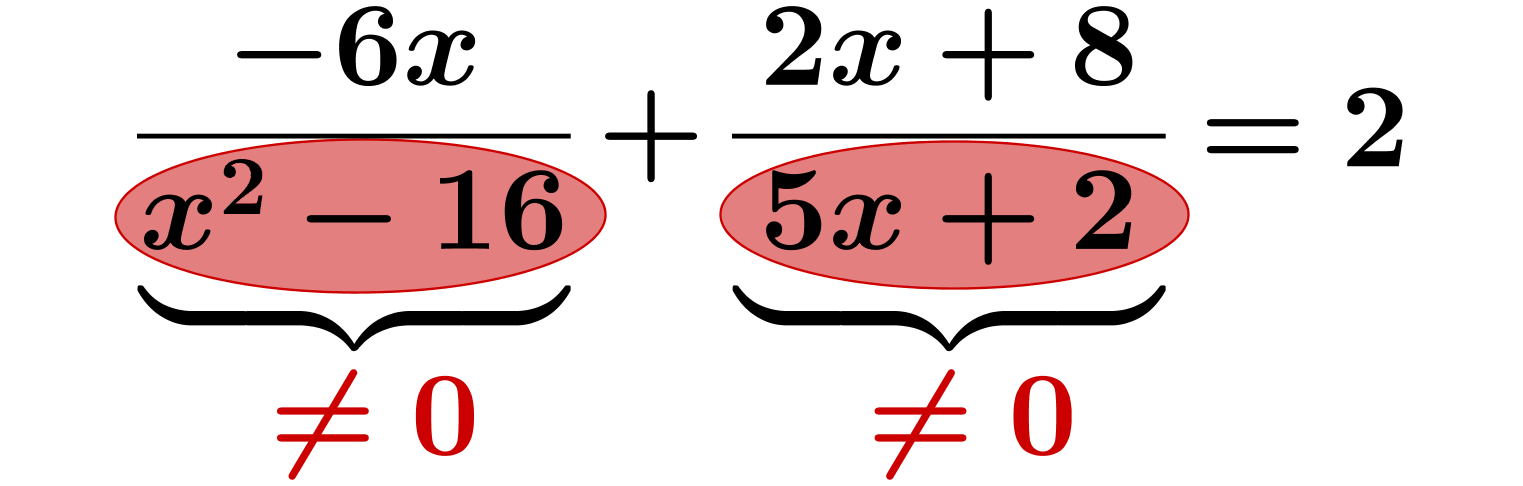
Beispiel einer Bruchgleichung Beide Nenner dürfen nicht Null werden.

Im Nenner eines Bruches darf niemals Null stehen. Alle Zahlen, für die sich beim Einsetzen in der Gleichung irgendwo im Nenner Null ergibt, müssen deshalb aus der Definitionsmenge einer Bruchgleichung ausgeschlossen werden.

Mathematische Schreibweise

Um Zahlen aus der Grundmenge auszuschließen, verwendet man das Mengenoperationszeichen $\setminus$ (also einen nach rückwärts gekippten Strich).

" $\setminus$ " bedeutet "ohne".
Danach kommen die ausgeschlossenen Zahlen.
Um diese Zahlen herum steht eine Mengenklammer: " $\left\{ … \right\}$ ".

Anmerkung zur Grundmenge

Als Grundmenge wird natürlich in der Regel die größtmögliche Zahlenmenge verwendet, die zur Verfügung steht. Je nach Klassenstufe und Lehrplan kann das aber entweder die Menge $\mathbb R$ der reellen Zahlen oder aber nur die Menge $\mathbb Q$ der rationalen Zahlen sein.

VorgehenBestimmung der Definitionsmenge

Für jeden der vorkommenden Brüche, schreibt man den Nenner heraus, setzt ihn gleich 0 und löst nach der Variablen auf.

Alle Zahlen, die man dabei als Lösungen erhält, muss man bei der Definitionsmenge ausschließen:

Beispiel: $D=\mathbb{R}\setminus\{\}$

Man schreibt die Grundmenge hin (meist $\mathbb Q$ oder $\mathbb R$ ), dann $\setminus$ ("ohne") und dann in Mengenklammern all die Zahlen, für die irgendein Nenner Null werden würde.

Allgemeines Vorgehen erklärt am Beispiel

Beschreibung	Beispiel
Für jeden der Brüche:	$\frac{-6x}{x^2-16}+\frac{2x+8}{5x+2}=2$
schreibt man den Nenner heraus,	$x^2-16$ $5x+2$
setzt ihn gleich 0	$x^2-16=0$ $5x+2=0$
und löst nach der Variablen auf.	$\begin {array}{rcll}x^2-16 &=&0 &\|+16;\ \\ x^2 &= &16 & \\ x=4 &\vee &x &=-4; \end{array}$ $\begin {array}{rcll}5x+2 &=&0 &\|-2 \\ 5x &= &-2&\|:5 \\ x &=&-\dfrac{2}{5} \end{array}$
Die so erhaltenen Zahlen muss man bei der Definitionsmenge aus der Grundmenge ausschließen.	Im Beispiel erhält man $\mathbb{D}= \mathbb{Q}\setminus \left\{-4;4;-\frac{2}{5} \right\}$ , falls die Grundmenge $\mathbb {Q}$ ist, bzw. $\mathbb{D}= \mathbb{R}\setminus \left\{-4;4;-\frac{2}{5} \right\}$ , falls die Grundmenge $\mathbb {R}$ ist.

Warum ist die maximale Definitionsmenge wichtig?

In der Regel wird vor dem Lösen der Bruchgleichung der Definitionsbereich (oder die Definitionsmenge) der Bruchgleichung bestimmt.

Wenn man später die Gleichung gelöst und ein Ergebnis erhalten hat, muss man nachprüfen, ob es überhaupt im Definitionsbereich liegt. Wenn es nicht darin enthalten ist, ist es nicht Lösung der Gleichung, auch wenn man ansonsten richtig gerechnet hat.

Übungsaufgaben: Maximale Definitionsmenge einer Bruchgleichung

Laden

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Definitionsmenge einer Bruchgleichung bestimmen

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?