Die Ableitung einer Umkehrfunktion lässt sich mithilfe der folgenden Formel bestimmen:
Video zur Ableitung einer Umkehrfunktion
Laden
Beispiel 1
Bestimmung der Ableitung von :
ist die Umkehrfunktion von , d.h. hier ist und
Da dann ist, ergibt sich für die Ableitung von :
Beispiel 2
Bestimmung der Ableitung von :
ist die Umkehrfunktion von , d.h. hier ist und
Mit ist dann:
Bemerkung
Die Ableitung der Wurzelfunktion lässt sich alternativ auch über die Regeln für Potenzfunktionen oder direkt über den Differenzenquotienten berechnen.
Erklärung
Man will die Ableitung von an der Stelle (rot gestrichelt) herausfinden, und betrachte dazu den Funktionsgraphen von :
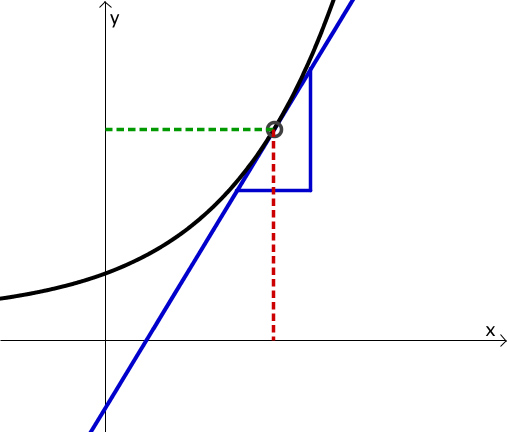
Nun spiegle man ihn an der Winkelhalbierenden des ersten und dritten Quadranten, sodass man den Graphen von vor sich hat:
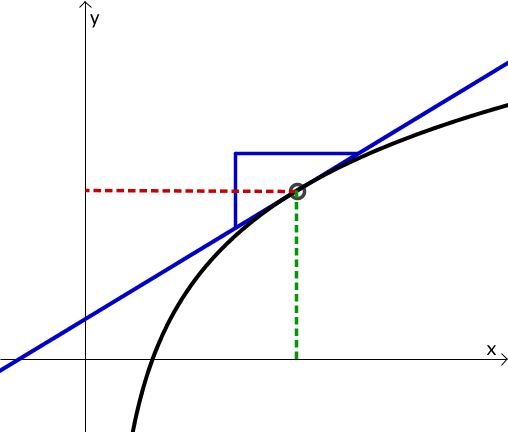
Man sieht, dass die Steigung der blauen Geraden im unteren Bild der Kehrwert der Steigung von der im oberen Bild ist, da sich die beiden Katheten im Steigungsdreieck vertauscht haben.
Im unteren Bild entspricht diese Steigung aber dem Funktionswert von an der grün gestrichelten Stelle .
Es ist also .
Ein Blick ins obere Bild zeigt aber: ist der Funktionswert von an der Stelle !
Damit ist
Herleitung der Formel
Diese Formel für die Ableitung der Umkehrfunktion kann man auch mithilfe der Kettenregel herleiten. Dafür nutzt man aus, dass
ist.
Wir können jetzt beide Seiten ableiten:
Mit der Kettenregel bekommen wir
und Umstellen der Formel nach liefert
.
