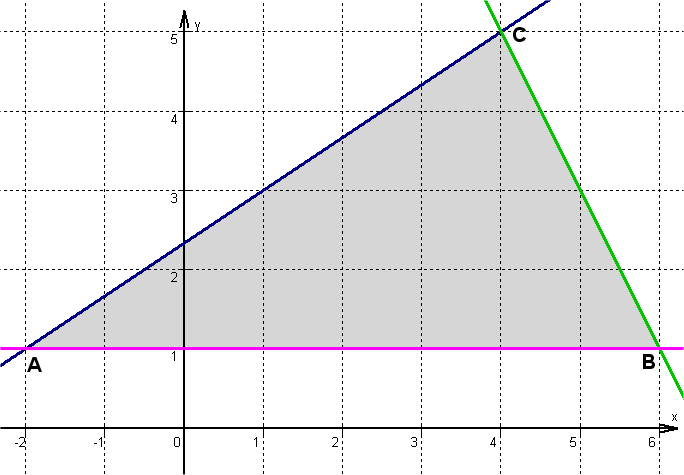
Gegeben sind die drei Punkte , und .
Stelle die Gleichung der Geraden , und auf.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Gerade AB:
und
Bestimme die Steigung mit dem Differenzenquotienten.
Die Gerade ist also parallel zur -Achse.
Der y-Achsenabschnitt ist also gleich der -Koordinate der beiden Punkte.
Setze zur Geradengleichung zusammen.
Gerade AC:
und
Bestimme die Steigung mit dem Differenzenquotienten.
Stelle die Gleichung für den y-Achsenabschnitt auf.
Setze einen Punkt, z.B. ein.
Löse nach auf.
Setze zur Geradengleichung zusammen.
Gerade BC:
und
Bestimme die Steigung mit dem Differenzenquotienten.
Stelle die Gleichung für den y-Achsenabschnitt auf.
Setze einen Punkt, z.B. ein.
Löse nach t auf.
Setze zur Geradengleichung zusammen.
Hast du eine Frage oder Feedback?
Berechne den Umfang des Dreiecks .
LEFür diese Aufgabe benötigst Du folgendes Grundwissen: Abstand von Punkten berechnen
Der Umfang des Dreiecks berechnet sich aus den Längen der Strecken zwischen den Punkten. Benutzte dazu die bekannte Formel.
Setze für jede Strecke zwei Punkte ein.
Seite AB:
Setze in die Formel ein. Beachte, dass für Längen nur positive Ergebnisse relevant sind.
Diese Seite hat also Länge 8.
Seite AC:
Setze in die Formel ein. Beachte, dass für Längen nur positive Ergebnisse relevant sind.
Diese Seite hat also etwa Länge 7,2.
Seite BC:
Setze in die Formel ein. Beachte, dass für Längen nur positive Ergebnisse relevant sind.
Diese Seite hat also etwa Länge 4,5.
Der Umfang ist gleich 8 + 7,2 + 4,5 = 19,7.
Hast du eine Frage oder Feedback?
Berechne den Flächeninhalt des Dreiecks .
FEFür diese Aufgabe benötigst Du folgendes Grundwissen: Fläche eines Dreiecks
Wähle AB als Grundseite, da diese parallel zur x-Achse ist. Dadurch ist die Höhe parallel zur y-Achse.
Höhe h ist gleich dem Abstand von zu .
Da die Höhe parallel zur y-Achse ist, berechnet sich der Abstand einfach durch Vergleich der y-Koordinaten.
Der Abstand des Punktes C von der Grundlinie ist
Eingesetzt in die Formel ergibt das:
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
