Taylorentwicklung
Im Gegensatz zur Schulmathematik, bei der meist nur die ersten drei Ableitungen nützlich sind, gibt es auch Anwendungsgebiete in der Mathematik, bei denen du beliebig viele Ableitungen brauchen kannst. Eine solche Anwendung ist die sogenannte Taylorentwicklung von Funktionen, die du in dieser Aufgabe kennenlernst.
Sei eine Funktion , sowie eine Funktionenschar mit maximalen Definitionsbereichen gegeben. Außerdem seien die folgenden Funktionen der Schar bekannt:
Zeige, dass für die gegebenen Scharfunktionen
gilt, wobei die -te Ableitung am Punkt ist und die Fakultät von angibt.
Die Funktion wird auch das -te Taylorpolynom an der Entwicklungsstelle genannt und man schreibt .
Gib den Funktionsterm von an.
In der folgenden Abbildung siehst du die Graphen der Funktionen und . Beschreibe die Abbildung und erläutere das Verhalten der Taylorpolynome für .
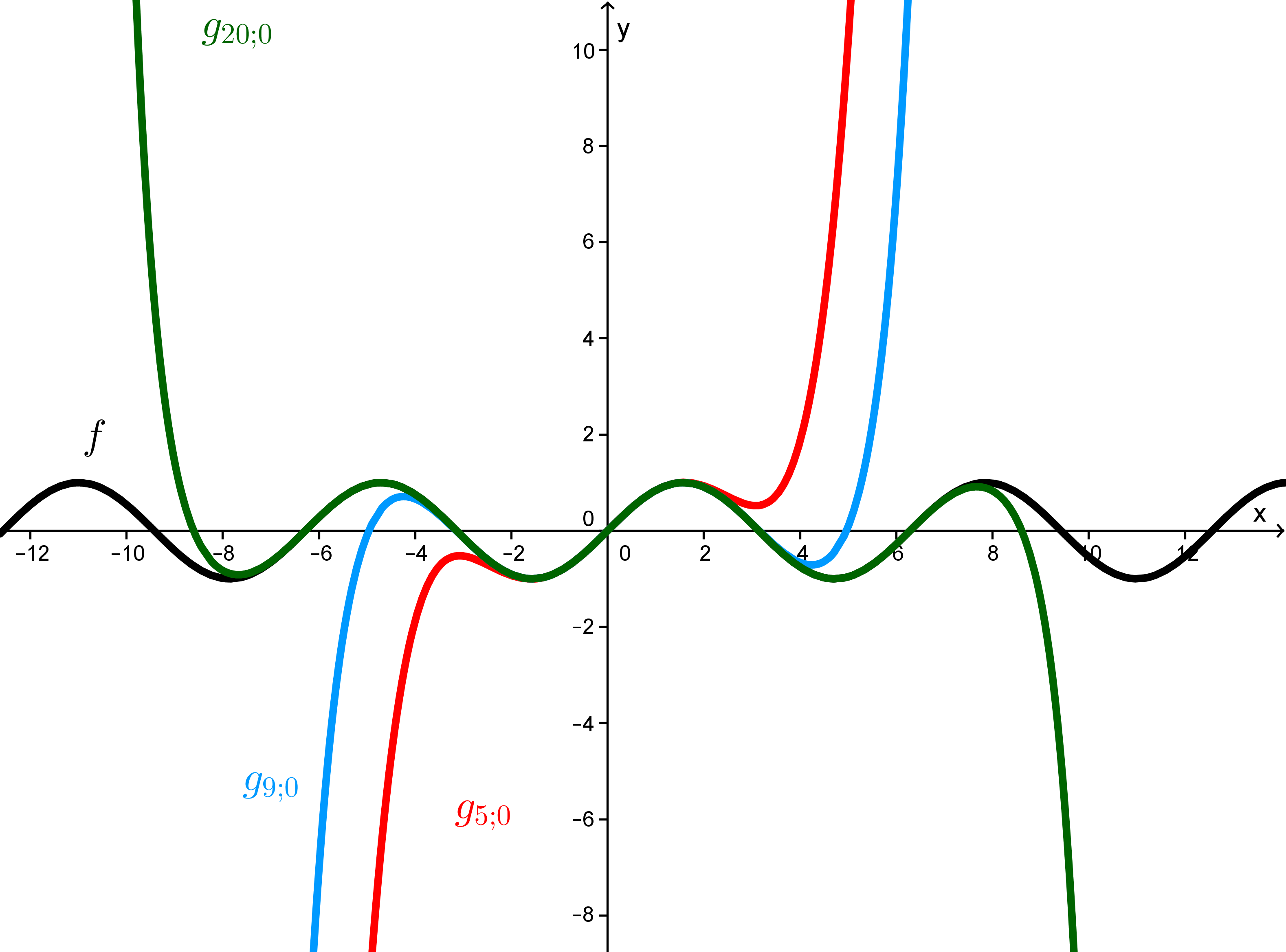
Wie sieht die Taylorentwicklung an der Entwicklungsstelle für die Funktion aus? Gib den Term des -ten Taylorpolynoms an oder beschreibe dessen Aussehen.
Gib die Taylorentwicklung der Funktion an der Entwicklungsstelle konkret an.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
