Schwierigere und weiterführende Aufgaben
Du willst dich herausfordern? Hier findest du schwierigere und weiterführende Aufgaben zur Taylorentwicklung und Volumenberechnung mit Integralen.
- 1
Taylorentwicklung
Im Gegensatz zur Schulmathematik, bei der meist nur die ersten drei Ableitungen nützlich sind, gibt es auch Anwendungsgebiete in der Mathematik, bei denen du beliebig viele Ableitungen brauchen kannst. Eine solche Anwendung ist die sogenannte Taylorentwicklung von Funktionen, die du in dieser Aufgabe kennenlernst.
Sei eine Funktion , sowie eine Funktionenschar mit maximalen Definitionsbereichen gegeben. Außerdem seien die folgenden Funktionen der Schar bekannt:
Zeige, dass für die gegebenen Scharfunktionen
gilt, wobei die -te Ableitung am Punkt ist und die Fakultät von angibt.
Die Funktion wird auch das -te Taylorpolynom an der Entwicklungsstelle genannt und man schreibt .
Gib den Funktionsterm von an.
In der folgenden Abbildung siehst du die Graphen der Funktionen und . Beschreibe die Abbildung und erläutere das Verhalten der Taylorpolynome für .
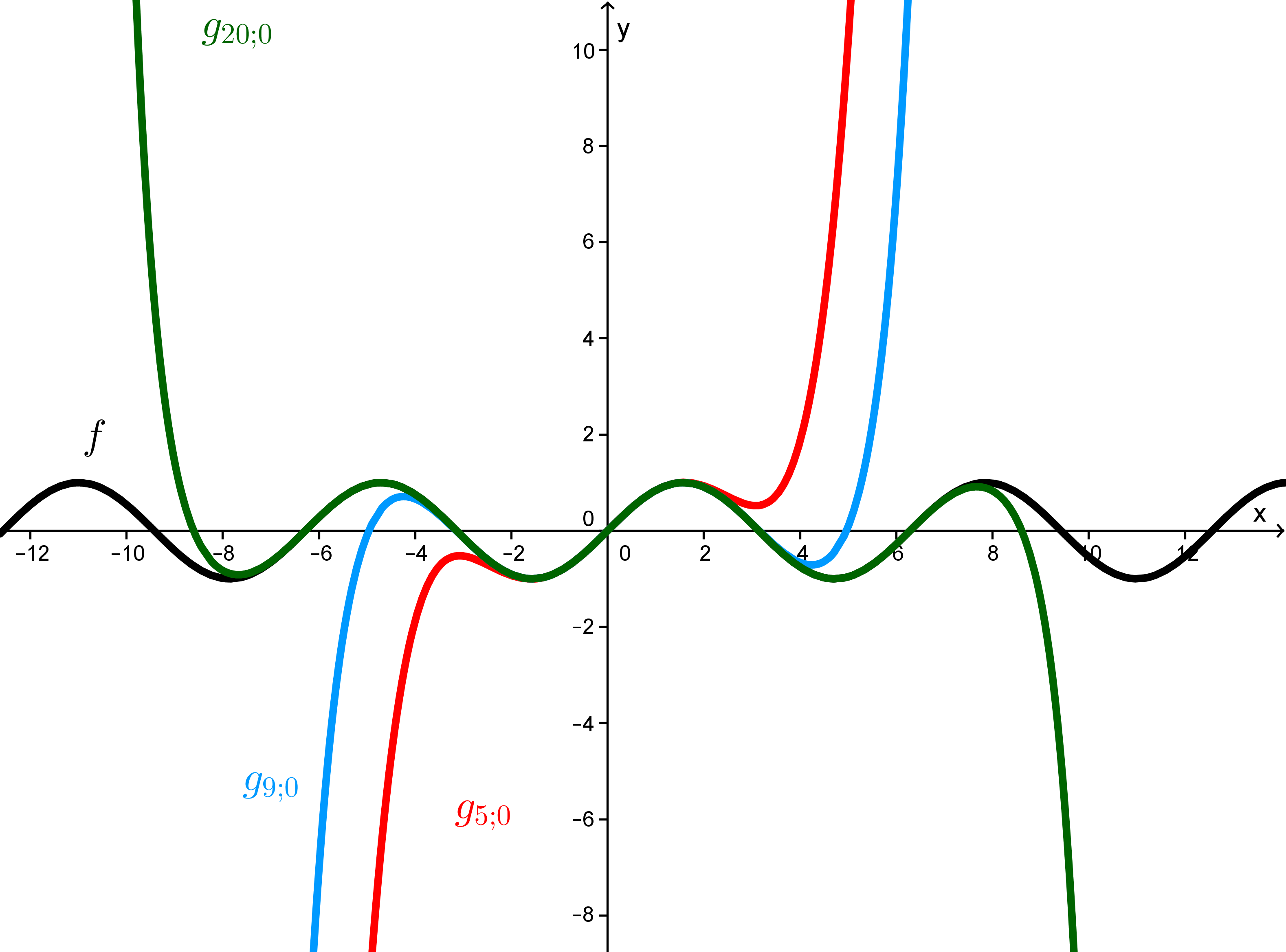
Wie sieht die Taylorentwicklung an der Entwicklungsstelle für die Funktion aus? Gib den Term des -ten Taylorpolynoms an oder beschreibe dessen Aussehen.
Gib die Taylorentwicklung der Funktion an der Entwicklungsstelle konkret an.
- 2
Volumenberechnungen mit Integralen
In der Schule lernst du das Berechnen von Flächen mittels Integralen kennen. Das Gleiche funktioniert aber auch eine Dimension höher. In Abbildung 1 siehst du einen Quader in einem dreidimensionalen Koordinatensystem. Es gilt für die Koordinaten:
.
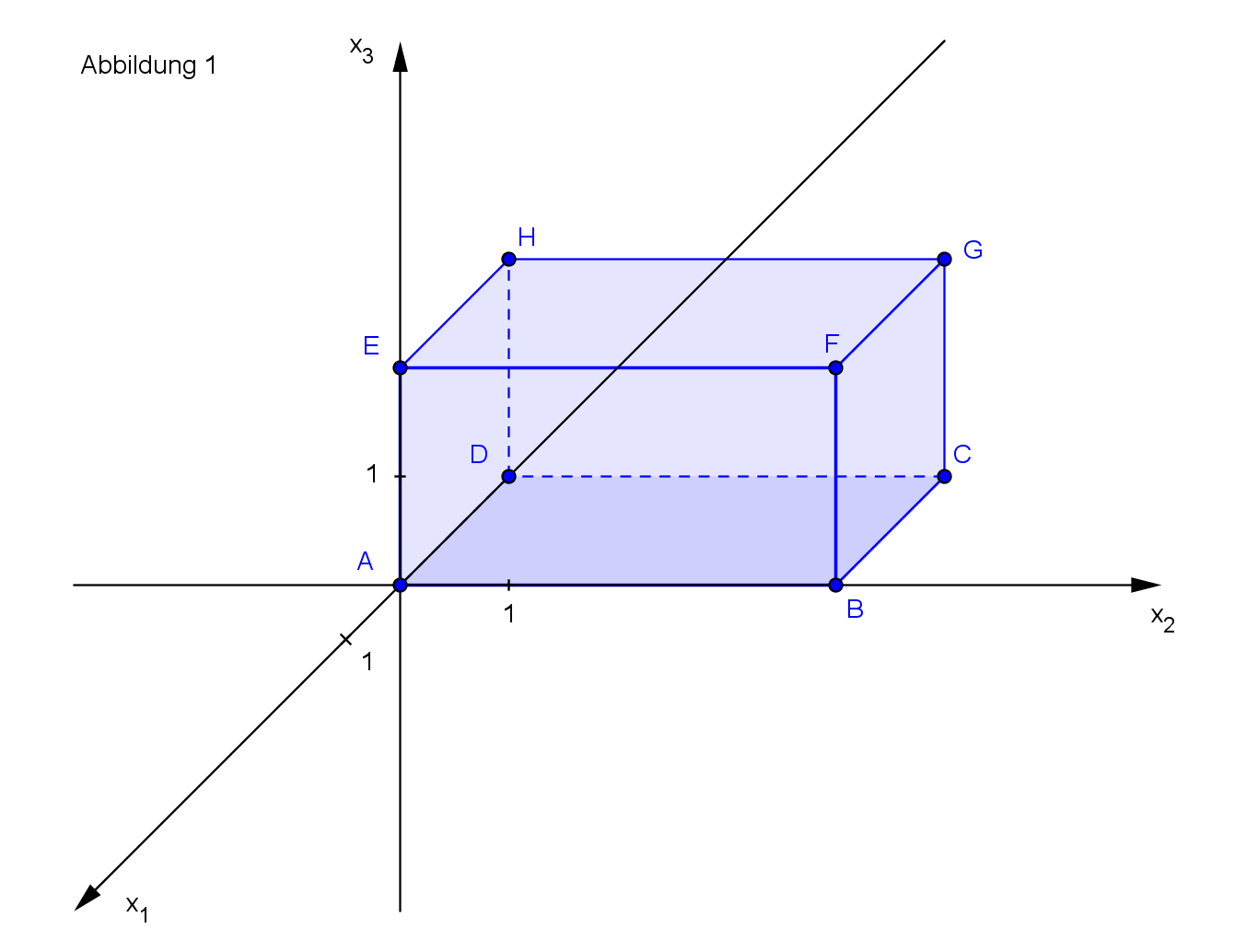
Berechne das Volumen des Quaders mit der Volumenformel.
Betrachte nun in Abbildung 2 die Vorderseite des Quaders. Die Seite ist der Graph der auf definierten Funktion .

Bestimme die Fläche der Quadervorderseite durch integrieren.
Nun wird das Bild "gedreht". In Abbildung 3 siehst du eine seitliche Ansicht des Quaders.

Die Vorstellung bei der Integration ist das schrittweise Ausfüllen der Fläche unter einem Graphen mit Strichen / Balken. Das Gleiche machst du jetzt mit der in die Zeichnung hineingehenden Fläche , um den Quader "auszufüllen".
Bestimme das Volumen des Quaders durch Integration mit dem Integranden .
Ausgehend vom Anfang ist die Volumenformel damit ein doppeltes Integral.
Die Volumenformel für einen Zylinder mit Höhe und Grundflächenradius lautet .
Erkläre, warum diese Formel richtig ist. (Hinweis: Überlege dir, wie der Zylinder nach und nach durch Strecken, Kreise, Flächen o. ä. ausgefüllt wird)
Betrachte jetzt die Volumenformel
Das Volumen welchen Körpers wird mit dieser Formel berechnet?
Zeige, dass die richtigen Ergebnisse liefert, indem du für und berechnest und mit dem Ergebnis der Volumenformel aus der Geometrie vergleichst.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
